Открытый резонатор: Открытый резонатор

Оптический резонатор — Википедия. Что такое Оптический резонатор

Оптический резонатор — совокупность нескольких отражающих элементов, образующих открытый резонатор (в отличие от закрытых объёмных резонаторов, применяемых в диапазоне СВЧ), формирующих стоячую световую волну. Оптические резонаторы являются одним из основных элементов лазеров, обеспечивая положительную обратную связь для обеспечения многократного прохождения лазерного излучения через активную среду, что приводит к усилению светового потока.

В оптическом диапазоне резонатор с размерами порядка длины волны не может быть применен в силу технологических трудностей и из-за резкого падения добротности; резонатор типа замкнутой металлической полости больших по сравнению с длиной волны размеров не может быть применен в силу высокой плотности его собственных колебаний, приводящих к потере резонансных свойств. Необходимы резонаторы с разреженным спектром собственных колебаний. Такими свойствами обладают открытые резонаторы, что и обуславливает их применение в оптическом диапазоне.

Свет многократно отражается, образуя стоячие волны с определенными резонансными частотами. Продольные моды отличаются, как правило, только частотой, в то время как поперечные моды имеют существенно различное распределение интенсивности в сечении луча. Наиболее часто используются оптические резонаторы, образованные двумя отражающими элементами, такими как зеркала или уголковые отражатели, и простейшим оптическим резонатором является интерферометр Фабри-Перо, состоящий из двух плоских параллельных зеркал. Однако для лазеров случай двух плоских зеркал используется не очень часто, ввиду сложности юстировки. Используются резонаторы со сферическими зеркалами. Такие резонаторы отличаются радиусом кривизны (следовательно и фокусным расстоянием) отражающих элементов и расстоянием между ними. Геометрические параметры резонатора выбираются исходя из требований устойчивости, а также других факторов, таких как, например, формирование наименьшей перетяжки оптического пучка.

Оптические резонаторы обычно конструируются таким образом, чтобы иметь наиболее высокую добротность (порядка 103−109{\displaystyle 10^{3}-10^{9}}): свет должен отражаться максимальное количество раз, не затухая, поэтому ширина резонансных пиков очень мала по сравнению с частотой излучения лазера.

Моды резонатора

Моды оптического резонатора Поперечные моды оптического резонатора со сферическими зеркалами Поперечные моды оптического резонатора с плоскими зеркалами

Свет в резонаторе многократно отражается от зеркал. Отраженные лучи интерферируют, что приводит к тому, что только определенные распределения полей на определенных частотах будут сохраняться в резонаторе, излучение на других частотах или с другим распределением будет подавлено за счет интерференции или быстро покинет резонатор. Распределения, которые повторяются при одном полном проходе резонатора являются наиболее стабильными и называются собственными модами или модами резонатора. Моды оптического резонатора подразделяют на две группы: продольные, отличающиеся частотой, и поперечные, которые отличаются как частотой, так и распределением поля в сечении пучка. Обычно основная поперечная мода представляет собой гауссовский пучок.

Исследования А. Фокса и Т. Ли в 1960-1961 гг. предоставили наглядную картину формирования собственных мод открытого резонатора методом рассмотрения изменений в распределении амплитуды и фазы первоначально плоской волны при её многократных последовательных проходах через резонатор. Анализ Фокса и Ли, выполненный ими для открытых резонаторов типа интерферометра Фабри-Перо в нескольких геометрических конфигурациях (прямоугольные плоские зеркала, круглые плоские зеркала), а также для конфокальных сферических и параболических зеркал, привел к следующим выводам:

1. Открытые резонаторы характеризуются дискретным набором колебательных мод.
2. Однородные плоские волны не являются нормальными модами открытых резонаторов
3. Электромагнитные волны, соответствующие собственным модам резонатора, почти полностью поперечны. Поэтому моды обозначаются символом ТЕМ.
4. Моды более высокого порядка имеют более высокие дифракционные потери, чем основная мода.
5. Для основной моды амплитуда поля сильно уменьшается к краям зеркала. Поэтому её дифракционные потери много меньше предсказываемых на основе представления об однородных плоских волнах и в реальных ситуациях пренебрежимо малы.

Частота моды пустого оптического резонатора с идеальными бесконечно большими зеркалами удовлетворяет соотношению:

Ωqnm=cL(πq+(1+n+m)arccos⁡g1g2){\displaystyle \Omega _{qnm}={\frac {c}{L}}(\pi q+(1+n+m)\arccos {\sqrt {g_{1}g_{2}}})}

Где Ωqnm{\displaystyle \Omega _{qnm}} — Угловая частота моды с индексами q,n,m. q — индекс продольной моды, n,m — индексы поперечной моды. c — скорость света. L — расстояние между зеркалами для плоского резонатора и половина периметра для кольцевого резонатора. g1,g2{\displaystyle g_{1},g_{2}} — g-параметры резонатора (см. #Устойчивость резонатора).

[1]

Типы резонаторов

Оптические резонаторы могут содержать большое количество отражающих и других элементов, но наиболее часто применяются двухзеркальные резонаторы, зеркала которых плоские или сферические. В зависимости от радиусов зеркал и их взаимного расположения выделяют следующие типы двухзеркальных резонаторов (R1{\displaystyle R_{1}} и R2{\displaystyle R_{2}} — радиусы кривизны зеркал):

• Плоскопараллельный (R1=R2=∞{\displaystyle R_{1}=R_{2}=\infty }) — так называемый резонатор Фабри-Перо. Широко используемой в лазерной технике разновидностью резонатора с плоскопараллельными зеркалами является резонатор с брегговскими отражателями, представляющими собой многослойные диэлектрические или полупроводниковые структуры.

• Конфокальный (R1=R2=L{\displaystyle R_{1}=R_{2}=L}). Конфокальный резонатор образован двумя одинаковыми сферическими зеркалами, фокусы F1{\displaystyle F_{1}}и F2{\displaystyle F_{2}} которых совпадают. Поле в таком резонаторе концентрируется около оси, что снижает дифракционные потери. Данный тип резонатора мало чувствителен к разъюстировке, однако объем активной области используется неэффективно.
• Полуконфокальный (R1=2L,R2=∞{\displaystyle R_{1}=2L,R_{2}=\infty }). Полуконфокальный резонатор образован одним плоским и одним сферическим зеркалом, радиус кривизны которого равен удвоенной длине резонатора. По своим свойствам он аналогичен конфокальному резонатору с удвоенной длиной.
• Концентрический (R1=R2=L/2{\displaystyle R_{1}=R_{2}=L/2}). Концентрический резонатор образован двумя сферическими зеркалами, оси и центры кривизны которых совпадают. В таких резонаторах дифракционные потери для неаксиальных мод быстро возрастают, что используется для селекции мод.
• Полуконцентрический (R1=L,R2=∞{\displaystyle R_{1}=L,R_{2}=\infty }). Образован одним сферическим зеркалом и одним плоским, по своим свойствам близок к концентрическому резонатору.

Устойчивость резонатора

Диаграмма устойчивости двухзеркальных резонаторов

Резонатор называется неустойчивым, когда произвольный луч, последовательно отражаясь от каждого из зеркал, удаляется на неограниченно большое расстояние от оси резонатора. Наоборот, резонатор, в котором луч остается в пределах ограниченной области, называется устойчивым. В резонаторе, образованном парой зеркал только для определенного диапазона значений длин резонатора и радиусов кривизны зеркал возможно выполнение условий обеспечивающих устойчивую локализацию света в резонаторе, в противном случае сечение пучка с каждым проходом будет увеличиваться, становясь больше размеров зеркал, и, в конечном итоге, будет потеряно.

Соотношение радиусов кривизны зеркал R1,R2{\displaystyle R_{1},R_{2}} и оптической длины резонатора L{\displaystyle L} для обеспечения устойчивости должно удовлетворять следующему соотношению:

0⩽(1−LR1)(1−LR2)⩽1. {\displaystyle 0\leqslant \left(1-{\frac {L}{R_{1}}}\right)\left(1-{\frac {L}{R_{2}}}\right)\leqslant 1.}

Введя обозначения

g1=1−LR1,g2=1−LR2{\displaystyle g_{1}=1-{\frac {L}{R_{1}}},\qquad g_{2}=1-{\frac {L}{R_{2}}}},

Оптический резонатор Википедия

Оптический резонатор — совокупность нескольких отражающих элементов, образующих открытый резонатор (в отличие от закрытых объёмных резонаторов, применяемых в диапазоне СВЧ), формирующих стоячую световую волну. Оптические резонаторы являются одним из основных элементов лазеров, обеспечивая положительную обратную связь для обеспечения многократного прохождения лазерного излучения через активную среду, что приводит к усилению светового потока.

В оптическом диапазоне резонатор с размерами порядка длины волны не может быть применен в силу технологических трудностей и из-за резкого падения добротности; резонатор типа замкнутой металлической полости больших по сравнению с длиной волны размеров не может быть применен в силу высокой плотности его собственных колебаний, приводящих к потере резонансных свойств. Необходимы резонаторы с разреженным спектром собственных колебаний. Такими свойствами обладают открытые резонаторы, что и обуславливает их применение в оптическом диапазоне.

Свет многократно отражается, образуя стоячие волны с определенными резонансными частотами. Продольные моды отличаются, как правило, только частотой, в то время как поперечные моды имеют существенно различное распределение интенсивности в сечении луча. Наиболее часто используются оптические резонаторы, образованные двумя отражающими элементами, такими как зеркала или уголковые отражатели, и простейшим оптическим резонатором является интерферометр Фабри-Перо, состоящий из двух плоских параллельных зеркал. Однако для лазеров случай двух плоских зеркал используется не очень часто, ввиду сложности юстировки. Используются резонаторы со сферическими зеркалами. Такие резонаторы отличаются радиусом кривизны (следовательно и фокусным расстоянием) отражающих элементов и расстоянием между ними. Геометрические параметры резонатора выбираются исходя из требований устойчивости, а также других факторов, таких как, например, формирование наименьшей перетяжки оптического пучка.

{9}}): свет должен отражаться максимальное количество раз, не затухая, поэтому ширина резонансных пиков очень мала по сравнению с частотой излучения лазера.

Моды резонатора

Моды оптического резонатора Поперечные моды оптического резонатора со сферическими зеркалами Поперечные моды оптического резонатора с плоскими зеркалами

Свет в резонаторе многократно отражается от зеркал. Отраженные лучи интерферируют, что приводит к тому, что только определенные распределения полей на определенных частотах будут сохраняться в резонаторе, излучение на других частотах или с другим распределением будет подавлено за счет интерференции или быстро покинет резонатор. Распределения, которые повторяются при одном полном проходе резонатора являются наиболее стабильными и называются собственными модами или модами резонатора. Моды оптического резонатора подразделяют на две группы: продольные, отличающиеся частотой, и поперечные, которые отличаются как частотой, так и распределением поля в сечении пучка.

Обычно основная поперечная мода представляет собой гауссовский пучок.

Исследования А. Фокса и Т. Ли в 1960-1961 гг. предоставили наглядную картину формирования собственных мод открытого резонатора методом рассмотрения изменений в распределении амплитуды и фазы первоначально плоской волны при её многократных последовательных проходах через резонатор. Анализ Фокса и Ли, выполненный ими для открытых резонаторов типа интерферометра Фабри-Перо в нескольких геометрических конфигурациях (прямоугольные плоские зеркала, круглые плоские зеркала), а также для конфокальных сферических и параболических зеркал, привел к следующим выводам:

1. Открытые резонаторы характеризуются дискретным набором колебательных мод.
2. Однородные плоские волны не являются нормальными модами открытых резонаторов
3. Электромагнитные волны, соответствующие собственным модам резонатора, почти полностью поперечны. Поэтому моды обозначаются символом ТЕМ.
4. Моды более высокого порядка имеют более высокие дифракционные потери, чем основная мода.
5. Для основной моды амплитуда поля сильно уменьшается к краям зеркала. Поэтому её дифракционные потери много меньше предсказываемых на основе представления об однородных плоских волнах и в реальных ситуациях пренебрежимо малы.

Частота моды пустого оптического резонатора с идеальными бесконечно большими зеркалами удовлетворяет соотношению:

Ωqnm=cL(πq+(1+n+m)arccos⁡g1g2){\displaystyle \Omega _{qnm}={\frac {c}{L}}(\pi q+(1+n+m)\arccos {\sqrt {g_{1}g_{2}}})}.

Где Ωqnm{\displaystyle \Omega _{qnm}} — Угловая частота моды с индексами q,n,m. q — индекс продольной моды, n,m — индексы поперечной моды. c — скорость света. L — расстояние между зеркалами для плоского резонатора и половина периметра для кольцевого резонатора. g1,g2{\displaystyle g_{1},g_{2}} — g-параметры резонатора (см. #Устойчивость резонатора).^[1]

Типы резонаторов

Оптические резонаторы могут содержать большое количество отражающих и других элементов, но наиболее часто применяются двухзеркальные резонаторы, зеркала которых плоские или сферические. В зависимости от радиусов зеркал и их взаимного расположения выделяют следующие типы двухзеркальных резонаторов (R1{\displaystyle R_{1}} и R2{\displaystyle R_{2}} — радиусы кривизны зеркал):

• Плоскопараллельный (R1=R2=∞{\displaystyle R_{1}=R_{2}=\infty }) — так называемый резонатор Фабри-Перо. Широко используемой в лазерной технике разновидностью резонатора с плоскопараллельными зеркалами является резонатор с брегговскими отражателями, представляющими собой многослойные диэлектрические или полупроводниковые структуры.

• Конфокальный (R1=R2=L{\displaystyle R_{1}=R_{2}=L}). Конфокальный резонатор образован двумя одинаковыми сферическими зеркалами, фокусы F1{\displaystyle F_{1}}и F2{\displaystyle F_{2}} которых совпадают. Поле в таком резонаторе концентрируется около оси, что снижает дифракционные потери. Данный тип резонатора мало чувствителен к разъюстировке, однако объем активной области используется неэффективно.
• Полуконфокальный (R1=2L,R2=∞{\displaystyle R_{1}=2L,R_{2}=\infty }). Полуконфокальный резонатор образован одним плоским и одним сферическим зеркалом, радиус кривизны которого равен удвоенной длине резонатора. По своим свойствам он аналогичен конфокальному резонатору с удвоенной длиной.
• Концентрический (R1=R2=L/2{\displaystyle R_{1}=R_{2}=L/2}). Концентрический резонатор образован двумя сферическими зеркалами, оси и центры кривизны которых совпадают. В таких резонаторах дифракционные потери для неаксиальных мод быстро возрастают, что используется для селекции мод.
• Полуконцентрический (R1=L,R2=∞{\displaystyle R_{1}=L,R_{2}=\infty }). Образован одним сферическим зеркалом и одним плоским, по своим свойствам близок к концентрическому резонатору.

Устойчивость резонатора

Диаграмма устойчивости двухзеркальных резонаторов

Резонатор называется неустойчивым, когда произвольный луч, последовательно отражаясь от каждого из зеркал, удаляется на неограниченно большое расстояние от оси резонатора. Наоборот, резонатор, в котором луч остается в пределах ограниченной области, называется устойчивым. В резонаторе, образованном парой зеркал только для определенного диапазона значений длин резонатора и радиусов кривизны зеркал возможно выполнение условий обеспечивающих устойчивую локализацию света в резонаторе, в противном случае сечение пучка с каждым проходом будет увеличиваться, становясь больше размеров зеркал, и, в конечном итоге, будет потеряно.

Соотношение радиусов кривизны зеркал R1,R2{\displaystyle R_{1},R_{2}} и оптической длины резонатора L{\displaystyle L} для обеспечения устойчивости должно удовлетворять следующему соотношению:

0⩽(1−LR1)(1−LR2)⩽1.{\displaystyle 0\leqslant \left(1-{\frac {L}{R_{1}}}\right)\left(1-{\frac {L}{R_{2}}}\right)\leqslant 1.}

Введя обозначения

g1=1−LR1,g2=1−LR2{\displaystyle g_{1}=1-{\frac {L}{R_{1}}},\qquad g_{2}=1-{\frac {L}{R_{2}}}},

удобно графически показать области устойчивости в координатах g1,g2{\displaystyle g_{1},g_{2}}. Тёмные области на рисунке отвечают значениям, при которых резонатор устойчив.

Неустойчивые резонаторы

Неустойчивые резонаторы можно подразделить на два класса: 1) резонаторы положительной ветви, которые удовлетворяют условию g1g2>1{\displaystyle g_{1}g_{2}>1}, и 2) резонаторы отрицательной ветви, которые соответствуют условию g1g2<0.{\displaystyle g_{1}g_{2}<0.} Отметим, что для устойчивого резонатора, соответствующего на плоскости g1,g2{\displaystyle g_{1},g_{2}} точке, которая расположена не очень близко к границе неустойчивости, размер пятна имеет тот же порядок, что и у конфокального резонатора, то есть, при длине резонатора порядка метра и для длин волн видимого диапазона размер пятна будет порядка или менее 1мм. При таком небольшом сечении моды выходная мощность (энергия) лазерного излучения, которую можно получить в одной поперечной моде, неизбежно оказывается ограниченной. В неустойчивых же резонаторах поле не стремится сосредоточиться вблизи оси, и в режиме одной поперечной моды можно получить большой модовый объем. Однако при этом возникает другая проблема, связанная с тем, что лучи стремятся покинуть резонатор. Поэтому соответствующие моды имеют значительно большие геометрические потери, чем моды устойчивого резонатора. Тем не менее, данное обстоятельство может быть обращено на пользу, если лучи, которые теряются на выходе резонатора, включить в полезное выходное излучение лазера.

Кольцевые резонаторы

Кольцево́й резона́тор — оптический резонатор, в котором свет распространяется по замкнутой траектории в одном направлении. Объёмные кольцевые резонаторы состоят из трёх или более зеркал, ориентированных так, что свет последовательно отражается от каждого из них, совершая полный оборот. Кольцевые резонаторы находят широкое применение в лазерных гироскопах и лазерах.

Селекция мод

Селекция мод — это совокупность методов, обеспечивающих режим, в котором резонатор поддерживает только одну или несколько избранных мод колебаний. В основе всех этих методов лежит создание неодинаковых для различных мод потерь в оптическом резонаторе или усиления в активной среде. Существует несколько способов, позволяющих проводить селекцию как продольных мод, поле которых испытывает осцилляции (перемены знака) вдоль оси резонатора, так и поперечных мод, поле которых осциллирует также и в поперечном направлении.

Селекцию поперечных мод используют обычно для создания генерации лишь на нулевой поперечной моде, имеющей минимальный диаметр и отличающейся гладким профилем интенсивности и минимальной расходимостью. Селекция осуществляется, как правило, помещением внутрь резонатора диафрагмы, затеняющей своими краями все поперечные моды, кроме нулевой. Наряду с этим для селекции поперечных мод иногда используют неустойчивые резонаторы, в которых размеры всех мод искусственно увеличиваются до такой степени, что роль диафрагм начинают играть зеркала резонатора или активный элемент. Возможны и другие способы — например, путём размещения в резонаторе фотонных кристаллов. Селекцию продольных мод используют главным образом для получения монохроматического излучения. Селекция за счёт неодинаковых потерь осуществляется помещением внутрь резонатора дополнительных полупрозрачных зеркал или дисперсионных элементов (призм, решёток, интерферометров).

Дополнительные зеркала вместе с основными образуют один или несколько дополнительных резонаторов, связанных с исходным. В генерацию выходят лишь те продольные моды исходного двухзеркального резонатора, которые наименее связаны с низкодобротным дополнительным резонатором. Дисперсионные элементы типа призм и решёток отклоняют под разными углами лучи с разными длинами волн. В итоге только для узкого спектра частот мод образуется высокодобротный резонатор. Внутрирезонаторные интерферометры осуществляют селекцию продольных мод за счёт того, что они обладают хорошей прозрачностью лишь для узких участков спектра мод. Селекция за счёт неодинаковости усиления осуществляется в основном в кольцевых твердотельных лазерах, в результате чего в них возникает однонаправленная генерация (бегущая волна). В этих условиях начинает сильно проявляться однородность уширения линии усиления активной среды и спектр генерации сужается до одной-двух мод.

Добротность оптических резонаторов

Колебательные системы обычно характеризуются добротностью Q. Добротность резонатора можно определить несколькими способами, которые эквивалентны при больших значениях добротности.^[2]

Применение оптических резонаторов

См. также

Примечания

1. ↑ Радина Т. В., Станкевич А. Ф. Резонансные и параметрические явления в задачах генерации и распространения лазерного излучения. — Санкт-Петербург: Издательство Санкт-Петербургского Государственного Университета, 2009. — С. 39-43. — 231 с. — ISBN 978-5-288-04965-1.
2. ↑ Архивированная копия (неопр.) (недоступная ссылка). Дата обращения: 1 июля 2015. Архивировано 24 сентября 2015 года.

3. Формирование и селекция поперечных мод в лазерных резонаторах : монография / А. В. Дегтярёв, В. А. Маслов, В. А. Свич, А. Н. Топков.  Х. : ХНУ имени В. Н. Каразина, 2017. – 212 с. ISBN 978-966-285-374-2

Оптический резонатор — Википедия. Что такое Оптический резонатор

Оптический резонатор — совокупность нескольких отражающих элементов, образующих открытый резонатор (в отличие от закрытых объёмных резонаторов, применяемых в диапазоне СВЧ), формирующих стоячую световую волну. Оптические резонаторы являются одним из основных элементов лазеров, обеспечивая положительную обратную связь для обеспечения многократного прохождения лазерного излучения через активную среду, что приводит к усилению светового потока.

В оптическом диапазоне резонатор с размерами порядка длины волны не может быть применен в силу технологических трудностей и из-за резкого падения добротности; резонатор типа замкнутой металлической полости больших по сравнению с длиной волны размеров не может быть применен в силу высокой плотности его собственных колебаний, приводящих к потере резонансных свойств. Необходимы резонаторы с разреженным спектром собственных колебаний. Такими свойствами обладают открытые резонаторы, что и обуславливает их применение в оптическом диапазоне.

Свет многократно отражается, образуя стоячие волны с определенными резонансными частотами. Продольные моды отличаются, как правило, только частотой, в то время как поперечные моды имеют существенно различное распределение интенсивности в сечении луча. {9}}): свет должен отражаться максимальное количество раз, не затухая, поэтому ширина резонансных пиков очень мала по сравнению с частотой излучения лазера.

Моды резонатора

Моды оптического резонатора Поперечные моды оптического резонатора со сферическими зеркалами Поперечные моды оптического резонатора с плоскими зеркалами

Свет в резонаторе многократно отражается от зеркал. Отраженные лучи интерферируют, что приводит к тому, что только определенные распределения полей на определенных частотах будут сохраняться в резонаторе, излучение на других частотах или с другим распределением будет подавлено за счет интерференции или быстро покинет резонатор. Распределения, которые повторяются при одном полном проходе резонатора являются наиболее стабильными и называются собственными модами или модами резонатора. Моды оптического резонатора подразделяют на две группы: продольные, отличающиеся частотой, и поперечные, которые отличаются как частотой, так и распределением поля в сечении пучка.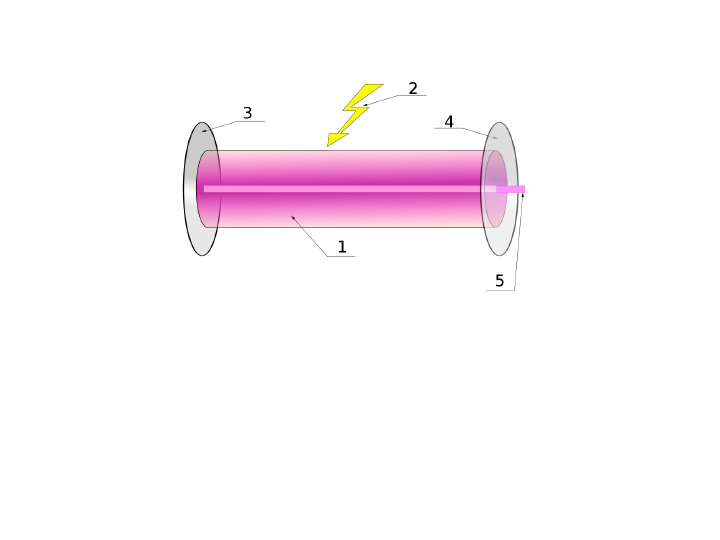 Обычно основная поперечная мода представляет собой гауссовский пучок.

Исследования А. Фокса и Т. Ли в 1960-1961 гг. предоставили наглядную картину формирования собственных мод открытого резонатора методом рассмотрения изменений в распределении амплитуды и фазы первоначально плоской волны при её многократных последовательных проходах через резонатор. Анализ Фокса и Ли, выполненный ими для открытых резонаторов типа интерферометра Фабри-Перо в нескольких геометрических конфигурациях (прямоугольные плоские зеркала, круглые плоские зеркала), а также для конфокальных сферических и параболических зеркал, привел к следующим выводам:

1. Открытые резонаторы характеризуются дискретным набором колебательных мод.
2. Однородные плоские волны не являются нормальными модами открытых резонаторов
3. Электромагнитные волны, соответствующие собственным модам резонатора, почти полностью поперечны. Поэтому моды обозначаются символом ТЕМ.
4. Моды более высокого порядка имеют более высокие дифракционные потери, чем основная мода.
5. Для основной моды амплитуда поля сильно уменьшается к краям зеркала. Поэтому её дифракционные потери много меньше предсказываемых на основе представления об однородных плоских волнах и в реальных ситуациях пренебрежимо малы.

Частота моды пустого оптического резонатора с идеальными бесконечно большими зеркалами удовлетворяет соотношению:

Ωqnm=cL(πq+(1+n+m)arccos⁡g1g2){\displaystyle \Omega _{qnm}={\frac {c}{L}}(\pi q+(1+n+m)\arccos {\sqrt {g_{1}g_{2}}})}

Где Ωqnm{\displaystyle \Omega _{qnm}} — Угловая частота моды с индексами q,n,m. q — индекс продольной моды, n,m — индексы поперечной моды. c — скорость света. L — расстояние между зеркалами для плоского резонатора и половина периметра для кольцевого резонатора. g1,g2{\displaystyle g_{1},g_{2}} — g-параметры резонатора (см. #Устойчивость резонатора).^[1]

Типы резонаторов

Оптические резонаторы могут содержать большое количество отражающих и других элементов, но наиболее часто применяются двухзеркальные резонаторы, зеркала которых плоские или сферические. В зависимости от радиусов зеркал и их взаимного расположения выделяют следующие типы двухзеркальных резонаторов (R1{\displaystyle R_{1}} и R2{\displaystyle R_{2}} — радиусы кривизны зеркал):

• Плоскопараллельный (R1=R2=∞{\displaystyle R_{1}=R_{2}=\infty }) — так называемый резонатор Фабри-Перо. Широко используемой в лазерной технике разновидностью резонатора с плоскопараллельными зеркалами является резонатор с брегговскими отражателями, представляющими собой многослойные диэлектрические или полупроводниковые структуры.

• Конфокальный (R1=R2=L{\displaystyle R_{1}=R_{2}=L}). Конфокальный резонатор образован двумя одинаковыми сферическими зеркалами, фокусы F1{\displaystyle F_{1}}и F2{\displaystyle F_{2}} которых совпадают. Поле в таком резонаторе концентрируется около оси, что снижает дифракционные потери. Данный тип резонатора мало чувствителен к разъюстировке, однако объем активной области используется неэффективно.
• Полуконфокальный (R1=2L,R2=∞{\displaystyle R_{1}=2L,R_{2}=\infty }). Полуконфокальный резонатор образован одним плоским и одним сферическим зеркалом, радиус кривизны которого равен удвоенной длине резонатора. По своим свойствам он аналогичен конфокальному резонатору с удвоенной длиной.
• Концентрический (R1=R2=L/2{\displaystyle R_{1}=R_{2}=L/2}). Концентрический резонатор образован двумя сферическими зеркалами, оси и центры кривизны которых совпадают. В таких резонаторах дифракционные потери для неаксиальных мод быстро возрастают, что используется для селекции мод.
• Полуконцентрический (R1=L,R2=∞{\displaystyle R_{1}=L,R_{2}=\infty }). Образован одним сферическим зеркалом и одним плоским, по своим свойствам близок к концентрическому резонатору.

Устойчивость резонатора

Диаграмма устойчивости двухзеркальных резонаторов

Резонатор называется неустойчивым, когда произвольный луч, последовательно отражаясь от каждого из зеркал, удаляется на неограниченно большое расстояние от оси резонатора. Наоборот, резонатор, в котором луч остается в пределах ограниченной области, называется устойчивым. В резонаторе, образованном парой зеркал только для определенного диапазона значений длин резонатора и радиусов кривизны зеркал возможно выполнение условий обеспечивающих устойчивую локализацию света в резонаторе, в противном случае сечение пучка с каждым проходом будет увеличиваться, становясь больше размеров зеркал, и, в конечном итоге, будет потеряно.

Соотношение радиусов кривизны зеркал R1,R2{\displaystyle R_{1},R_{2}} и оптической длины резонатора L{\displaystyle L} для обеспечения устойчивости должно удовлетворять следующему соотношению:

0⩽(1−LR1)(1−LR2)⩽1.{\displaystyle 0\leqslant \left(1-{\frac {L}{R_{1}}}\right)\left(1-{\frac {L}{R_{2}}}\right)\leqslant 1.}

Введя обозначения

g1=1−LR1,g2=1−LR2{\displaystyle g_{1}=1-{\frac {L}{R_{1}}},\qquad g_{2}=1-{\frac {L}{R_{2}}}},

удобно графически показать области устойчивости в координатах g1,g2{\displaystyle g_{1},g_{2}}. Тёмные области на рисунке отвечают значениям, при которых резонатор устойчив.

Неустойчивые резонаторы

Неустойчивые резонаторы можно подразделить на два класса: 1) резонаторы положительной ветви, которые удовлетворяют условию g1g2>1{\displaystyle g_{1}g_{2}>1}, и 2) резонаторы отрицательной ветви, которые соответствуют условию g1g2<0.{\displaystyle g_{1}g_{2}<0.} Отметим, что для устойчивого резонатора, соответствующего на плоскости g1,g2{\displaystyle g_{1},g_{2}} точке, которая расположена не очень близко к границе неустойчивости, размер пятна имеет тот же порядок, что и у конфокального резонатора, то есть, при длине резонатора порядка метра и для длин волн видимого диапазона размер пятна будет порядка или менее 1мм. При таком небольшом сечении моды выходная мощность (энергия) лазерного излучения, которую можно получить в одной поперечной моде, неизбежно оказывается ограниченной. В неустойчивых же резонаторах поле не стремится сосредоточиться вблизи оси, и в режиме одной поперечной моды можно получить большой модовый объем. Однако при этом возникает другая проблема, связанная с тем, что лучи стремятся покинуть резонатор. Поэтому соответствующие моды имеют значительно большие геометрические потери, чем моды устойчивого резонатора. Тем не менее, данное обстоятельство может быть обращено на пользу, если лучи, которые теряются на выходе резонатора, включить в полезное выходное излучение лазера.

Кольцевые резонаторы

Кольцево́й резона́тор — оптический резонатор, в котором свет распространяется по замкнутой траектории в одном направлении. Объёмные кольцевые резонаторы состоят из трёх или более зеркал, ориентированных так, что свет последовательно отражается от каждого из них, совершая полный оборот. Кольцевые резонаторы находят широкое применение в лазерных гироскопах и лазерах.

Селекция мод

Селекция мод — это совокупность методов, обеспечивающих режим, в котором резонатор поддерживает только одну или несколько избранных мод колебаний. В основе всех этих методов лежит создание неодинаковых для различных мод потерь в оптическом резонаторе или усиления в активной среде. Существует несколько способов, позволяющих проводить селекцию как продольных мод, поле которых испытывает осцилляции (перемены знака) вдоль оси резонатора, так и поперечных мод, поле которых осциллирует также и в поперечном направлении.

Селекцию поперечных мод используют обычно для создания генерации лишь на нулевой поперечной моде, имеющей минимальный диаметр и отличающейся гладким профилем интенсивности и минимальной расходимостью. Селекция осуществляется, как правило, помещением внутрь резонатора диафрагмы, затеняющей своими краями все поперечные моды, кроме нулевой. Наряду с этим для селекции поперечных мод иногда используют неустойчивые резонаторы, в которых размеры всех мод искусственно увеличиваются до такой степени, что роль диафрагм начинают играть зеркала резонатора или активный элемент. Возможны и другие способы — например, путём размещения в резонаторе фотонных кристаллов. Селекцию продольных мод используют главным образом для получения монохроматического излучения. Селекция за счёт неодинаковых потерь осуществляется помещением внутрь резонатора дополнительных полупрозрачных зеркал или дисперсионных элементов (призм, решёток, интерферометров).

Дополнительные зеркала вместе с основными образуют один или несколько дополнительных резонаторов, связанных с исходным. В генерацию выходят лишь те продольные моды исходного двухзеркального резонатора, которые наименее связаны с низкодобротным дополнительным резонатором. Дисперсионные элементы типа призм и решёток отклоняют под разными углами лучи с разными длинами волн. В итоге только для узкого спектра частот мод образуется высокодобротный резонатор. Внутрирезонаторные интерферометры осуществляют селекцию продольных мод за счёт того, что они обладают хорошей прозрачностью лишь для узких участков спектра мод. Селекция за счёт неодинаковости усиления осуществляется в основном в кольцевых твердотельных лазерах, в результате чего в них возникает однонаправленная генерация (бегущая волна). В этих условиях начинает сильно проявляться однородность уширения линии усиления активной среды и спектр генерации сужается до одной-двух мод.

Добротность оптических резонаторов

Колебательные системы обычно характеризуются добротностью Q. Добротность резонатора можно определить несколькими способами, которые эквивалентны при больших значениях добротности.^[2]

Применение оптических резонаторов

См. также

Примечания

1. ↑ Радина Т. В., Станкевич А. Ф. Резонансные и параметрические явления в задачах генерации и распространения лазерного излучения. — Санкт-Петербург: Издательство Санкт-Петербургского Государственного Университета, 2009. — С. 39-43. — 231 с. — ISBN 978-5-288-04965-1.
2. ↑ http://www.rfe.by/media/kafedry/kaf2/publications/afonenko/tema6-1.pdf

A Квази-Яги антенна с пониженной печатью, симметрично нагруженная элементами Меандрового открытого комплементарного кольцевого резонатора (MOCSRR) Джошуа Андерсон.

Презентация на тему: «Квази-Яги антенна с уменьшенной частотой, симметрично нагруженная элементами Меандрового открытого комплементарного кольцевого резонатора (MOCSRR), Джошуа Андерсон». — Стенограмма презентации:

1 Квази-Яги-антенна с пониженной частотой печати, симметрично нагруженная элементами Меандрового открытого дополнительного разъемного кольцевого резонатора (MOCSRR) Джошуа Андерсон Кай Джонсон Коди Саттерли Эндрю Линч Бенджамин Д.Браатен * Департамент ECE Государственный университет Северной Дакоты Фарго, Северная Дакота, США.

2 1) Введение и предыстория 2) Квази-Яги антенна с пониженной частотой 3) Результаты измерений и моделирования 4) Обсуждение и рекомендации 5) Заключительные темы

3 Введение и предыстория [1] А. Велес, Ф. Аснар, Дж. Бонаш, М.К. Валаскес-Ахумада, Дж. Мартель и Ф. Мартин, «Открытые комплементарные кольцевые резонаторы (OCSRR) и их применение в широкополосных полосовых фильтрах CPW», IEEE Microwave and Wireless Component Letters, vol. 19, нет. 4, pp. 197–199, апрель 2009 г. Элемент открытого дополнительного разъемного кольцевого резонатора (OCSRR) [1]:

4 [2] Б. Д. Браатен, «Новая компактная радиочастотная метка-антенна УВЧ, разработанная с использованием последовательно соединенных частиц с открытым комплементарным кольцевым резонатором (OCSRR)», IEEE Transactions on Antennas and Propagation, vol.58, нет. 11, ноя 2010, стр. 3728-3733. Элемент OCSRR использовался для разработки небольших резонансных антенн [2]: Введение и общие сведения

5 Элемент меандрового открытого комплементарного кольцевого резонатора (MOCSRR) [3]: [3] Б.Д. Браатен и М.А. Азиз, «Использование частиц меандрового открытого комплементарного кольцевого резонатора (MCOSRR) для разработки компактной UHF RFID-антенны», IEEE Antenna and Wireless Письма о пропаганде, т.9, 2010, стр. 1037-1040.

6 Введение и фоновая структура CPW, используемая для измерения элемента MOCSRR:

7 Введение и фон Печатный элемент MOCSRR: S-параметры [4]: ​​L eq = 9,25 нГн C eq = 5,1 пФ fo = 735 МГц [4] Б. Д. Браатен, М. А. Азиз, М. Дж. Шредер и Х. Ли, «Меандровое открытое дополнительное разрезное кольцо. резонаторные частицы (MOCSRR), реализованные с использованием копланарных волноводов », Труды Международной конференции IEEE по беспроводным информационным технологиям и системам, Гонолулу, Гавайи, август.28 — 3 сентября 2010 г.

8 Квази-яги с пониженной частотой A = 131,4 мм B = 145,98 мм a = 22,27 мм b = 17,7 мм c = 1,3 мм d1 = 52,0 мм f = 40,98 мм i = 66,0 мм j = 12,0 мм k = 41,0 мм m = 5,8 мм n = 9,08 мм u = 4,45 мм α = 48,28 мм β = 15,91 мм Подложка: Толщина: 1,27 мм Диэлектрическая проницаемость: 10,2

9 Пониженная частота квази-яги W = 6.88 мм H = 6,73 мм d2 = 2,45 мм g = 0,22 мм h = 4,53 мм p = 0,26 мм q = 0,32 мм r = 1,94 мм s = 0,17 мм t = 0,27 мм v = 0,19 мм L eq = 5,25 нГн C eq = 5,6 пФ fo = 2,2 ГГц Прибл. удвоенная рабочая частота.

10 Результаты измерений и моделирования Оригинальная незагруженная квази-яги антенна [5]. Новая загруженная квази-яги антенна. [5] С. Чен и П. Хсу, «Модифицированная квази-яги антенна с широкополосным микрополосковым питанием», Беспроводная связь и прикладная вычислительная электромагнетизм, август.2005, стр. 208-211.

12 Результаты измерений и моделирования Измерение оригинальной квази-яги антенны. Рабочая частота 1,2 ГГц.

Спектральный многополосный резонатор

О SMR:

На первый взгляд, SMR работает как обычный шестиполосный графический эквалайзер: шесть частотных полосовых фильтров смешиваются вместе с помощью ползунков. Резонанс / Q — переменный, который изменяет «звонкость» или ширину полос.

Но на этом сравнение заканчивается. Частота каждого канала рассматривается как нота в гамме, а шесть полос образуют аккорд. Вращайте ручку поворота, и «ноты» кружатся вокруг шкалы, возвращаясь к низу, когда достигают вершины. Отрегулируйте Spread и расстояние (интервал) между изменениями каждой ноты. Триггеры для движения вверх / вниз, входы CV для выбора последовательности и масштабирования позволяют гибко управлять с помощью внешних модулей. Morph, который автоматически перекрестно затухает между частотами, вместе с регулируемым Slew позволяет ритмичным тактовым частотам управлять SMR как развивающимся резонансным фильтром с регулируемой скоростью.

При максимальном резонансе / добротности SMR можно поразить как гонг или маримбу, введя часы или триггеры. Частота каждого канала дискретизирована по шкале: красивые аккорды, неземные тона и жуткая атмосфера текут легко. При более низком резонансе SMR может выделить определенные полосы частот и развернуть их по спектру.

Два частотных гнезда 1 В на октаву позволяют отслеживать четные и / или нечетные полосы и создавать плавающие мелодии поверх развивающихся аккордов или сложных перкуссионных мембранных звуков.

Сохраните настройки в один из шести банков хранения и мгновенно загрузите их. При запуске SMR мгновенно переходит к последним сохраненным настройкам. Цветовую схему огней можно отрегулировать, поэтому, если вы предпочитаете все белые огни на модуле, вы можете использовать это (или все красные, или радуги, пастели и т. Д.)!

Основные характеристики:

• Шесть каналов фильтров, выбранных из двадцати активных фильтров, отображаемых на световом кольце
• Переменная «Q» (резонанс) варьируется от классической полосы пропускания до ультрарезонансного звона.
• Кольцо из 20 полноцветных огней отображает частоты фильтра
• Частоты фильтра перемещаются по шкале с помощью вращения и распространения
• Вращение «раскручивает» частоты вокруг шкалы
• Spread контролирует разрыв между соседними полосами
• Morph создает плавное затухание с переменной скоростью при изменении частот фильтра
• Кнопки блокировки предотвращают изменение частоты каждого канала (также можно заблокировать резонанс)
• Регуляторы Freq Nudge для создания эффектов отстройки или точной настройки частоты
• Частотный вход CV (1 В / октава) для четных и нечетных диапазонов (поворотный переключатель выбирает одно или несколько каналов управления)
• Стерео входы и выходы разбивают группы на равные / разногласия для иммерсивного стерео поля
• Выходы спектрального контента для каждого канала (Env Out) позволяют вокодирование (спектральная передача)
• Быстрая или медленная скорость отслеживания для выходных сигналов Envelope CV или выбираемый режим выхода триггера полезны для извлечения ритма из музыки
• Слайдеры и разъемы CV контролируют уровень каждого фильтра
• Переключатель поворота применяет ограничение поворота к разъемам уровня CV, что предотвращает щелчки от часов или триггеров
• Каждый банк имеет 11 шкал по 20 частот / нот в каждой.
• Программируемые пользователем шкалы (выбор октавы, хроматической ноты и микротональных настроек для каждой ноты в шкале)
• Банк шкал для настроек Western, Indian, Chromatic, Micro-tonal, Equal tempered, Just.
• Rotation / Spread перемещается по всему банку или может быть ограничено одним масштабом
• Белый шум нормализован по входам, поэтому SMR можно использовать без внешнего сигнала

Расширенные функции

• Программируйте собственный масштаб.Частоту каждой из 20 нот можно назначить, установив октаву, полутон, а также грубый и тонкий микротон. В пользовательском банке можно постоянно сохранять до 11 весов
• Отрегулируйте цветовую схему светодиодов. Выберите заранее запрограммированную цветовую схему или создайте свою собственную, используя ползунки для установки значений красного / зеленого / синего цветов. Пользовательские цветовые схемы можно сохранять навсегда
• Сохраните настройки в одном из шести банков параметров. Положение ноты, выбор шкалы и банка, значение Q, настройки блокировки и цветовую схему можно сохранить и вызвать на лету.При запуске SMR загружает настройки из последнего сохраненного банка.
• Дополнительный альтернативный тип фильтра для более экспоненциального затухания при щелчке и других тембральных качеств. Разъемы Freq больше не отслеживают 1 В / октаву в этом режиме.
• Светодиоды ползунка могут быть назначены для отображения уровня для каждого канала (комбинация положения ползунка и CV на гнезде) или ограничения для каждого канала.

Эксперименты с дефектными конструкциями заземления для спаренных полосовых фильтров разомкнутого контура

В этом методе дефектные конструкции заземления на печатной плате используются для создания С-образных разомкнутых контуров.Разомкнутые контуры резонируют из-за емкости через прорезь и индуктивности через рот. Два резонатора соединены друг с другом небольшой «щелью» в С-образной щели (щель в щели — это металл). Радиомощность помещается в один резонансный открытый контур путем размещения микрополосковой линии поверх него. Когда частота входящей РЧ-мощности равна частоте, достаточно высокой для того, чтобы соответствовать и резонировать в разомкнутом контуре, она затем соединяется со следующим и выводится через микрополоску поверх него.

Чтобы настроить их, вы увеличиваете емкость, делая паз тоньше, и увеличиваете индуктивность, делая выступ c-образной формы больше.

Эти конструкции имеют то преимущество, что они могут быть очень маленькими по сравнению с длиной волны (0,2 * 0,13 длины волны) и иметь мало периодических / гармонических характеристик. Но из-за того, как они «включаются» при достаточно высокой частоте, они лучше блокируют полосу ниже полосы пропускания, чем выше.

Это моя реализация в EM-симуляторе и, в конечном итоге, в kicad, общей концепции проекта из статьи Ахмеда Бутейдара «Разработка BPF из компактного DGS LPF», опубликованной 30 августа 2016 года.

Окончательный размер составлял 6,7 * 4 см на FR4 толщиной 1,6 мм для 900-930 МГц -40 дБ обратных потерь (-3 дБ в диапазоне 800-1100 МГц) и вносимых потерь 0,5 дБ при 900-930 МГц.

А вот простой ДГС БПФ оказался не очень. Поэтому я объединил методы из нескольких других статей и закончил создание АРД с разомкнутым контуром в разомкнутом контуре с моим собственным новым методом микрополосковой связи и гораздо более высокими характеристиками. Это можно увидеть на гифке справа и под привязкой к странице «Yo dawg» в меню ниже.

[комментарий к этому сообщению] Добавьте «/ @say / ваше сообщение здесь» к URL-адресу в адресной строке и нажмите Enter.

Ну, в основном потому, что кто-то (вроде) попросил меня разработать полосовой фильтр, но я не знал, как это сделать. Поэтому я подумал, что попробую сделать такой для своих собственных трансиверов беспроводной локальной сети, которые используют диапазон 902–928 МГц в качестве учебного опыта. Многие предлагали шпильки и другие конструкции, но я хотел что-то маленькое и без гармоник. После серии поисков «электрически малая полосовая планарная печатная плата» и чтения множества не совсем подходящих статей, чтобы получить представление об этой области, я сузил ее до DGS, нашел вышеуказанную статью и перешел к ней.

Моделирование

Причуды и советы по сонету

Я * настоятельно * рекомендую вам выбрать размер сетки, который имеет чистые кратные. Я обычно начинаю с 0,25 мм и использую миллиметры как единицы. И никогда не пытайтесь использовать центрирующий инструмент, горизонтальный, вертикальный или и то, и другое. Это создаст конструкции, которые смещены относительно сетки и вызовут всевозможные проблемы. Центрировать вручную.

Для того, чтобы использовать что-то кроме плоского металлического прямоугольника в качестве заземляющего слоя в Sonnet, вам нужно перейти в конфигурацию «Схема-> Диэлектрик», а затем добавить еще один слой воздуха ниже диэлектрического слоя печатной платы.После этого у вас будет 3 слоя: 0, 1 и GND. 0 — это верхний металл, 1 — это земля печатной платы, а GND — это металл виртуальной металлической коробки, которая окружает все симуляции Sonnet. Для того, чтобы вновь созданный слой «земли» слоя 1 работал, он * должен * быть хотя бы где-то подключен к фактическому заземлению.

Создание резонаторов ДГС

Я не был уверен в том, какие размеры потребуются для ~ 915 МГц, поэтому я просто взорвал его. Я также только что догадался о точной форме вырезанных резонаторов с С-образным зазором в плоскости заземления.Я решил, что квадраты подойдут, и они сработали. Я просто смотрел на общие соотношения из статьи Ахмеда, а затем моделировал их, чтобы увидеть, что произойдет. Моя первая попытка была отличной полосой пропускания около 1400-1600 МГц. Так что это просто означало увеличивать размер всего за несколько итераций, пока я не добрался до 900 МГц

.

Это всего две важные вещи, о которых следует помнить, когда вы начинаете. Ширина паза определяет емкость в резонаторе, а отверстие С-образного паза определяет индуктивность.Сохраняйте ширину щели небольшой и сначала оптимизируйте ее. Затем настройте, регулируя высоту рта.

---

Начиная с

Обратите внимание на толщину верхнего и нижнего краев заземляющего слоя на этом. Это произошло потому, что мне пришлось увеличить размер резонатора, но я не хотел изменять размер коробки, потому что это означало бы перецентрирование и балансировку всего вручную. Эти тонкие края привели к снижению производительности.

---

Подойдя ближе, я понял, что могу точно настроить частоту прохода вверх или вниз, либо уменьшив размер «устья» С-образного резонатора, либо увеличив его.Кроме того, внешнее кольцо заземляющего слоя (слой 1) имеет значение для резонансной частоты. Чем уже внешнее кольцо проводника вокруг резонаторов, тем на более высокой частоте он будет резонировать. Таким образом, вы можете увеличить размер внешней заземляющей поверхности, чтобы снизить резонансную частоту. Эти два параметра, наряду с размером С-образного корпуса резонатора, позволяют довольно хорошо контролировать резонансную частоту полосы пропускания.

Микрополоска сверху

Я всегда использую 1.6-миллиметровый диэлектрик FR4, так как он самый дешевый в производстве и подходит для моих целей. Это означает, что для микрополоски 50 Ом ширина должна быть 2,54 мм. Но это не подходит для сетки. Вместо этого я использую следы 2,5 мм. Это дает следы 55 Ом, что находится в пределах допусков производителя и прочего.

Длина микрополоски над резонаторами на слое заземления прямо пропорциональна связи. Если она очень короткая и не сильно выступает над ними с обеих сторон, то полученная полоса пропускания имеет тенденцию разделяться на два пика.У меня не было способа вычислить, сколько связи мне нужно, поэтому я просто повторял и постепенно увеличивал длину, пока результаты моделирования не стали хорошими. Я также заметил, что по мере увеличения размера резонатора мне нужно было увеличить * пропорцию * выступа дорожек над резонатором для поддержания единой пиковой полосы пропускания.

Отступление о масштабировании полосы пропускания DGS для более низких частот / больших длин волн

Но вы можете продвигать только длину выступа микрополоски.В конце концов они перемещаются так близко друг к другу, что высокие частоты могут преодолевать промежуток за счет емкостной связи. Вот что произошло, когда я попытался масштабировать дизайн до 440 МГц.

Итак, приступим к поиску. Я снова обратился к фразе: «Увеличьте сцепление микрополосковой передачи по сравнению с резонаторным DGS». Именно там я нашел * другую * статью на mwrf.com под названием DGS Resonators Form Compact Filters, в которой было предложено решение.

По-видимому, вы можете сместить микрополосковую линию вниз от центра резонаторов к краю, поместив ее поверх самого зазора вдоль дна, и более сильная связь достигается с меньшей длиной следа.К сожалению, в моем моделировании этого не произошло. Я даже попытался полностью изменить дизайн, который копировал ту асимметричную форму резонатора, которую они использовали, но не мог ее воспроизвести. Это может быть просто другая вещь, которая работает только на очень высоких частотах (то есть> 2 ГГц), где микрополосковые следы велики по сравнению с резонатором.

Поскольку симуляторы с частотой 900 МГц меньше по размеру и работают намного быстрее, я протестировал их там. На графике ниже показаны мои результаты при попытке постепенно сместить микрополосковую трассу вниз к нижнему краю.Сначала отклик расщепляется, затем он сдвигает частоту вверх и быстро уходит совсем. Черные — средняя позиция по умолчанию. Розовая и синяя позиции — это след непосредственно рядом с нижним краем и немного ниже нижнего края соответственно.

Сдвиг микрополосковой дорожки на 3 мм от середины к нижнему краю

Другие попытки увеличить связь, такие как добавление ступеней импеданса и такие вещи, как меандровые линии, не дали результата.

[много сим позже…] Все мои предыдущие проекты провалились, потому что у меня было фундаментальное непонимание того, как они работают, и поэтому я неправильно масштабировал вещи. Я все время предполагал, что вырезанная прорезь работает по принципу бабинета; чтобы прорезь была равна его зеркальному отображению проводника в свободном пространстве. Так что для большей длины волны щель тоже должна быть больше.

Но что действительно имело значение, так это емкость в гнезде. И по мере того, как я увеличивал масштаб, ширина слота становилась очень маленькой. А малая емкость вызывает резонанс на более высоких частотах, поэтому возникает обратный эффект.Вместо этого размер слота нужно было сохранить маленьким, вместо того, чтобы увеличивать его по мере того, как я сдвигал целевую частоту вниз.

Как показано на графиках ниже, связи все еще недостаточно, но ее можно распознать как приличную, хотя и широкую полосу пропускания.

Конструкция полосы пропускания целевой частоты 430–450 МГц

Вынимаю гербер и помещаю в кикад для подготовки к изготовлению.

Герберы из сонета

Поскольку я обратил внимание на ограничения сетки и не использовал инструменты центрирования, и поскольку эта конструкция использовала все пространство блока моделирования, экспорт герберов был легким, и мне не пришлось увеличивать разрешение сетки с 0.25 мм до экспорта.

Герберы в Kicad

Чтобы импортировать герберы из Sonnet, вы открываете gerbview, выбираете оба слоя в диалоговом окне импорта файла и выбираете, который должен быть передним медным (F.cu), а какой — заземленным (B.cu). Я ошибся в первый раз, но при второй попытке было достаточно просто изменить направление. Затем File-> Export to pcbnew и сохраните как файл .kicad_pcb.

Герберы из кикада

После открытия созданного файла .kicad_pcb все, что оставалось, это выровнять импортированные структуры по сетке kicad, а затем применить полную плату F.Маска и B. Маска с помощью инструмента «Многоугольник» (чтобы паяльная маска не применялась), затем обведите плату с помощью инструмента «Линия» на слое Edge.Cuts. Это помогает создать одну линию, затем выбрать линию, перейти к свойствам и установить ширину линии на что-то маленькое, например 0,05, чтобы вы могли более четко видеть, где края доски находятся по углам, при создании других линий.

После этого он просто экспортирует с помощью кнопки «График». Я следил за очень полезным руководством в oshpark, чтобы узнать, какие параметры установить.И поскольку на этой плате нет переходных отверстий, я не создавал файл сверления

.

Затем он просто заархивировал полученные файлы из «Plot» и загрузил их в компанию, производящую печатные платы. И ждем 2-4 недели. Эта часть все еще продолжается.

Или был, это 2 недели спустя, и платы прибыли.

В то время как характеристики полосы пропускания DGS и ее нижней полосы задерживания были приемлемыми, слабая верхняя полоса задерживания продолжала меня беспокоить. Так что, продолжая делать обзор литературы, я продолжал наталкиваться на все эти статьи о метаматериалах причудливых штанов, использующих резонаторы с разъемным кольцом.На мой взгляд, они выглядят как разомкнутый контур в разомкнутом контуре, повернутый на 180 градусов. Я решил попробовать.

При его реализации я заметил, что у меня есть более широкая область максимальной плотности тока по середине. С моими перпендикулярными микрополосковыми следами я просто тратил большую часть их, и у меня все еще были проблемы с откликом фильтра, который был слабым и разделился на два пика. Потом меня осенило: что, если я сделаю след параллельно высокой плотности тока?

Юбка Dat.

Как вы можете видеть на скриншоте ниже, он работал очень хорошо.Ну, не изначально. Сначала это привело к некоторому интенсивному гармоническому поведению. Но, подумав некоторое время (и попробовав несколько подталкиваний в ту и другую сторону, расширяя и укорачивая, я решил попробовать еще один трюк, о котором читал. Изменив направление микрополосковой дорожки в каждом резонаторе, но заставив их поворачиваться в разные стороны, я мог посмотреть, смогу ли я заставить их работать в разных режимах (положительный или отрицательный). И это сработало. Гармонические отклики исчезли, за исключением небольшого скачка около 2 ГГц, где он был раньше.

Характеристики полосы пропускания ниже, но все еще ниже -15 дБ S11, что приемлемо. И частота немного сдвинулась вверх из-за повышенной нагрузки внутреннего разомкнутого контура. Но это просто означает, что мне придется сделать * немного * меньшего размера. Или, что более вероятно и проще: увеличить размер окружающей заземляющей плоскости.

Но оказывается, что увеличение размера заземляющего слоя не помогает при разработке SRR * вообще *. Похоже, что нет зависимости от ширины заземляющего слоя вокруг него.Также нет центрального металлического заземления внутри открытых контуров. Просто вроде как обычная полоска висит. Будет ли это все еще DGS, когда он не использует принцип бабинета и не хватает так много заземляющих плоскостей? Наверное, нет.

Я, честно говоря, не знаю, как это назвать, знаю, но знаю, что когда я изменил дизайн, чтобы снова добавить металлизацию по центру и сделать его чисто слот-режимом, это не сработало.

Оптимизация

Приведенный выше сюжет и поворот трассы были моим первым приблизительным предположением.Ничего более. После небольшой настройки длины я смог улучшить отклик и полностью устранить расщепление, а также увеличить глубину надреза (две стороны медали).

К kicad

Каждый раз, когда я разрабатываю эти фильтры, я делаю все возможное, чтобы сделать их как можно меньше. В итоге они настолько малы, что ставить на них разъемы SMA почти стыдно, так как это увеличивает площадь на треть.

С ними 5см * 3,7см. Это может показаться не таким уж большим, но по сравнению с оригиналом это намного больше места.А моделирование переходных отверстий требует много дополнительных вычислений в Sonnet при проверке того, что конечные пусковые площадки SMA не изменяют отклик.

Сейчас * фактически * на 910 МГц

За исключением того, что приведенный выше пример не был для 900-930 МГц. У него была центральная частота 960 МГц. Поэтому я переделал дизайн (рассчитал, что мне нужно было увеличить размер элементов SRR на 5%) и повторно реализовал в Sonnet. После небольшой настройки длин микрополосков я снова, наконец, получил хорошую полосу пропускания на 900-930 МГц.

Оборудование? Скоро в продаже …

Для ясности, это измерение досок в свободном пространстве; без металлической коробки (зазор 1 см сверху / снизу), как требуется для соответствия параметрам sim. Производительность на верхнем конце полосы заграждения ухудшается, а сама полоса пропускания едва приемлема только при -2,9 дБ S21 и только -19 дБ S11. Тем не менее, по крайней мере, это точно на целевой частоте.

Это был очень быстрый макет корпуса, сделанный из медной ленты с еще прикрепленной бумажной подложкой.Пайки не было, но с каждой стороны был ровный зазор по 1 см. На этот раз я установил шкалы одинакового размера и выровнял их, чтобы график не был глупым.

В этом я просверлил несколько отверстий под небольшим углом, так что печатная плата была немного наклонена. Кроме того, на задней стороне DGS есть только 5 мм свободного пространства вместо 10, как должно было бы. Это была еще одна срочная работа. Из-за слишком малого наклона и / или разноса резонаторный отклик расщепляется. Один переместился на низкий, а другой слишком высокий примерно на + и — 10 МГц соответственно.

С другой стороны, вносимые потери были незначительно улучшены, а глубина верхнего нуля была значительно улучшена (-10 дБ), что значительно расширило полосу пропускания.

Сделал еще 3 дизайна для более высоких частот. Пока собрал и протестировал только двухдиапазонный. Этот дизайн с самого начала был чем-то вроде компромисса, но это нормально. Я почти уверен, что смогу вернуть верхнюю часть S11 на свое место, немного припилив ножки, чтобы увеличить емкость по отношению к земле коробки.

Два способа улучшить оптическое зондирование с использованием различных методов резонатора

Структуры, называемые оптическими резонаторами, улавливают свет на определенных частотах. Когда окружающая среда такого резонатора возмущается, эти частоты сдвигаются, что позволяет использовать оптические резонаторы в качестве датчиков. а, Hodaei et al. сообщают о датчике, который состоит из трех связанных кольцевых резонаторов (красные стрелки). Авторы используют золотые нагревательные элементы как для точной настройки датчика, так и для имитации возмущений.б. Напротив, Chen et al. используйте один тороидальный резонатор и соедините свет, который движется по часовой стрелке (синяя стрелка) и против часовой стрелки (желтая стрелка). Авторы используют два наконечника волокна для настройки датчика и наконечник другого типа для внесения возмущений. c. В обычных датчиках сдвиг частоты, вызванный возмущением, прямо пропорционален силе возмущения (серая линия). Hodaei et al. и Chen et al. демонстрируют, что частотный сдвиг в их чувствительных устройствах масштабируется с кубическим корнем (красная линия) или квадратным корнем (синяя линия) из силы возмущения, соответственно.Это приводит к значительному улучшению масштабирования чувствительности таких датчиков по сравнению с обычными устройствами. Кредит: Микаэль К. Рехтсман, Nature 548, 161–162 (10 августа 2017 г.) doi: 10.1038 / 548161a

(Phys.org) — Две независимые группы, работающие над исследованиями, направленными на улучшение оптического восприятия, использовали методы, которые включают соединение двух или более режимов света таким образом, что их моды и соответствующие им частоты сливаются, что приводит к большей чувствительности. В первую очередь команда Вашингтонского университета в Санкт-Петербурге.Университет Лоис и Отто-фон-Герике в Магдебурге, Германия, соединил три традиционных датчика для более точной настройки. Во втором эксперименте команда из Университета Центральной Флориды и Технологического университета Мичигана использовала только один резонатор, но объединила свет, распространяющийся в обоих направлениях вокруг него. Обе команды опубликовали статьи с описанием своих усилий и результатов в журнале Nature . Микаэль Рехтсман из Университета штата Пенсильвания предлагает статью News & Views, в которой описываются методы оптического зондирования и работа, проделанная двумя командами, в одном номере журнала.

Как отмечает Рехтсман, оптические датчики используются во множестве приложений, которые связаны с очень небольшими механическими колебаниями или изменениями температуры. Они также используются при работе с наночастицами или при анализе биомолекул. Однако у всех таких датчиков есть одна проблема — их производительность ограничена силой исследуемых возмущений. В этом новом усилии обе исследовательские группы стремились преодолеть это ограничение путем объединения режимов света, позволяя им объединяться — это происходит в местах, называемых «исключительными точками», и они возникают только в так называемых эрмитовых системах.В таких системах, как показали предшествующие исследования, потеря фотонов является главной особенностью, в отличие от обычных систем, в которых верно обратное. В любом случае результатом является повышенная чувствительность, что, конечно, приводит к большей точности.

Первым делом исследователи соединили три кольцевых датчика вместе, а затем добавили под ними золотые нагревательные элементы для точной настройки датчиков и имитации возмущений. Во второй попытке исследователи использовали только один датчик в форме кольца, но направили свет вокруг него в обоих направлениях (как по часовой, так и против часовой стрелки) одновременно, чтобы вызвать слияние.Затем они использовали наконечник волокна для точной настройки датчика и второй наконечник, чтобы вызвать возмущения.

Оба метода, как отмечает Рехтсман, имеют компромисс между точной настройкой и чувствительностью, и остается вопрос, можно ли изменить один или оба варианта для достижения еще более высокой чувствительности.

---

Три команды находят способ измерения частот с гораздо большей точностью, чем предыдущие методы.

---

Дополнительная информация: 1.Weijian Chen et al. Исключительные точки улучшают восприятие в оптическом микрополости, Nature (2017). DOI: 10.1038 / nature23281

Аннотация
Датчики играют важную роль во многих аспектах повседневной жизни, например, инфракрасные датчики в системах домашней безопасности, датчики частиц для мониторинга окружающей среды и датчики движения в мобильных телефонах. Высококачественные оптические микрополости являются главными кандидатами для приложений зондирования из-за их способности усиливать взаимодействие света и вещества в очень ограниченном объеме.Примеры таких устройств включают механические преобразователи, магнитометры, одночастичные абсорбционные спектрометры3 и микрополостные датчики для определения размеров отдельных частиц и обнаружения объектов нанометрового масштаба, таких как отдельные наночастицы и атомарные ионы. Обычно очень малое возмущение вблизи оптического микрополости приводит либо к изменению ширины линии, либо к сдвигу частоты или расщеплению резонанса, которые пропорциональны силе возмущения. Здесь мы демонстрируем альтернативную схему зондирования, с помощью которой можно повысить чувствительность микрополостей при работе с неэрмитовыми спектральными вырождениями, известными как исключительные точки.В наших экспериментах мы используем два наноразмерных рассеивателя для настройки резонатора микротороида в режиме шепчущей галереи, в котором свет распространяется вдоль вогнутой поверхности путем непрерывного полного внутреннего отражения, точно и контролируемым образом в исключительные точки. Целевой наноразмерный объект, который впоследствии попадает в исчезающее поле полости, возмущает систему из ее исключительной точки, что приводит к расщеплению частот. Из-за топологии комплексного квадратного корня вблизи исключительной точки это расщепление частоты масштабируется как квадратный корень из силы возмущения и, следовательно, больше (для достаточно малых возмущений), чем расщепление, наблюдаемое в традиционных схемах зондирования неисключительных точек.Наша демонстрация исключительной чувствительности с повышенной точечной точностью открывает путь для датчиков с беспрецедентной чувствительностью.

2. Хоссейн Ходэй и др. Повышенная чувствительность в исключительных точках высшего порядка, Nature (2017). DOI: 10.1038 / nature23280

Аннотация
Неэрмитовские вырождения, также известные как исключительные точки, недавно появились как новый способ спроектировать реакцию открытых физических систем, то есть тех, которые взаимодействуют с окружающей средой.Они соответствуют точкам в пространстве параметров, в которых собственные значения базовой системы и соответствующие собственные векторы одновременно сливаются1, 2, 3. В оптике было показано, что резкий характер фазовых переходов, возникающих вокруг исключительных точек, приводит ко многим интригующим таких явлений, как индуцированная потерями прозрачность4, однонаправленная невидимость5, 6, слияние полос7, 8, топологическая хиральность9, 10 и селективность лазерных мод11, 12. Недавно было показано, что бифуркационные свойства неэрмитовых вырождений второго порядка могут обеспечивать средство повышения чувствительности (частотных сдвигов) резонансных оптических структур к внешним возмущениям13.Особый интерес представляет использование исключительных точек даже более высокого порядка (выше второго порядка), которые, в принципе, могут еще больше усилить эффект возмущений, что приведет к еще большей чувствительности. Хотя все большее количество теоретических исследований посвящается таким вырождениям более высокого порядка 14, 15, 16, их экспериментальная демонстрация в оптической области до сих пор остается неуловимой. Здесь мы сообщаем о наблюдении исключительных точек более высокого порядка в устройстве связанных резонаторов — в частности, тройной, симметричной по четности и времени фотонной лазерной молекулы — с тщательно подобранным распределением усиления-потерь.Мы изучаем систему в спектральной области и обнаруживаем, что частотная характеристика, связанная с этой системой, подчиняется зависимости кубического корня от наведенных возмущений показателя преломления. Наша работа прокладывает путь к использованию неэрмитовых вырождений в таких областях, как фотоника, оптомеханика10, микроволны9 и атомная физика17, 18.

© 2017 Phys.org

Ссылка : Два способа улучшить оптическое зондирование с помощью различных резонаторных технологий (2017, 10 августа) получено 21 января 2021 г.