Как устроена матричная оптика: — Журнал Движок.
Постепенный переход на светодиодные источники света в автомобилях уже несомненная тенденция. Лампы накаливания в ближайшем будущем останутся уделом устаревших конструкций. А сейчас высокоэффективные и долговечные фары постепенно отвоевывают позиции у традиционных. В маломощных осветительных приборах светодиоды уже вытеснили конкурентов, а вот в области головного света сражение еще идет. И основное оружие светодиодов — матричная оптика конструкции Hella.
Просто заменить газоразрядный или галогенный источник света на светодиоды — идея не новая. Еще в 2008 году подобная система появилась на машинах Lexus LS, а сейчас построенная по тому же принципу головная оптика стала базовой на многих массовых автомобилях. Например, новый кроссовер Skoda Kodiaq оснащен ею в базовой комплектации, как и соплатформенный VW Tiguan. На базе подобной конструкции можно создать даже адаптивное освещение, и оно не будет ничем принципиально отличаться от использующего газоразрядные источники света.
Качественный головной свет автомобиля должен быть не только ярким, но и освещать исключительно необходимые зоны. Кроме того, не слепить встречных водителей, выделять важные объекты и при этом учитывать особенности человеческого глаза в отношении контрастности освещения и светотеневой границы.
Адаптивное головное освещение на базе единого источника света во многом решает эти сложности, но настоящий прорыв возможен только при использовании матричного освещения, когда за каждую зону отвечает отдельный источник света с регулируемой яркостью, а управляется система интеллектуальным модулем, способным распознавать объекты перед машиной и регулировать освещенность различных зон по ситуации. И именно по этому пути пошла компания Hella при разработке своих матричных светодиодных модулей адаптивного освещения.
Идея использовать много фар для освещения нескольких зон перед машиной в случае традиционных источников света сталкивается с габаритными ограничениями. И газоразрядные источники света, и лампы накаливания имеют достаточно крупные размеры рабочей области и требуют объемной оптической системы.
И газоразрядные источники света, и лампы накаливания имеют достаточно крупные размеры рабочей области и требуют объемной оптической системы.
В случае со светодиодным освещением такая проблема не стоит. Если отказаться от использования сменных светодиодных модулей, то на небольшой плате можно разместить более 50 светодиодов, а поскольку их световой поток имеет явную направленность, то подобная матрица диодов отлично работает с компактной и простой оптической системой.
На практике в оптике Audi Matrix LED с 25 светодиодами адаптивного освещения они собраны в сменные модули по пять светодиодов в каждом, и еще пять модулей используются для статического освещения — ближнего света и статического бокового. В следующем поколении оптических систем Hella, которые с 2016 года устанавливаются на машины Mercedes, применяется целых 84 светодиода на единой плате.
Перспективная LED-оптика разработки Hella по-прежнему имеет «всего» 25 светодиодов на единой плате, но за счет использования в оптической системе фары проекционного LCD-дисплея с разрешением 30 тыс. пикселей с матрицей 100х300 число контролируемых зон освещения возрастает на порядок.
пикселей с матрицей 100х300 число контролируемых зон освещения возрастает на порядок.
Сложность подобной конструкции легко недооценить. При тех же габаритах, что и у традиционной фары, внутри матричная LED-оптика и ее система управления устроены на порядок сложнее. Чтобы не быть голословным, рассмотрим конструкцию и ее возможности на примере оптики Audi Matrix LED для модели A8 в кузове D4 2013 года. Не самой новой, но зато одной из самых распространенных в России и имеющей много общего со светодиодной матричной оптикой других машин Audi. На следующих поколениях и для других моделей, скорее всего, будет уже лазерный источник света.
Возможности и конструкция
Помимо конструкции самой оптической системы, важную роль для работы адаптивного освещения играет конструкция системы управления. В случае с матричной оптикой самым важным датчиком системы является LiDAR — дальномер оптического диапазона, позволяющий системе управления получить предоставления обо всех источниках света и объектах в зоне освещения головной оптики. Так же используются данные навигационной системы, датчики скорости автомобиля, дождя и освещенности и данные ассистента ночного видения, если он есть в автомобиле. На основании этих данных блок управления может использовать один из множества режимов работы.
Так же используются данные навигационной системы, датчики скорости автомобиля, дождя и освещенности и данные ассистента ночного видения, если он есть в автомобиле. На основании этих данных блок управления может использовать один из множества режимов работы.
Дальний свет для движения по автомагистрали включается на основании данных навигационной системы. В этом случае система Matrix Beam включает узкий луч с максимальной дальностью освещения, наилучшим образом подходящий для ночных поездок на высокой скорости.
Ближний свет с классической асимметричной формой светового пучка использует 15 отдельных светодиодов в каждой фаре и включается в населенных пунктах. Может применяться отдельно от адаптивного освещения. Дальняя зона освещения реализуется отдельным набором светодиодов и может быть отключена для реализации туристического или всепогодного режима.
Туристический режим используется при движении в странах с левосторонним движением для машин, созданных для движения правостороннего. Он позволяет уменьшить асимметрию светового луча при включенном режиме ближнего света. Включается режим или автоматически, по данным навигационной системы, или вручную, через меню мультимедийной системы.
Он позволяет уменьшить асимметрию светового луча при включенном режиме ближнего света. Включается режим или автоматически, по данным навигационной системы, или вручную, через меню мультимедийной системы.
Конструкцию основной оптической системы фары можно увидеть на рисунке, но помимо нее в конструкцию входят также модуль указателя поворота (разумеется, со светодиодами), модуль охлаждения, причем со сменным вентилятором, и внутренняя проводка.
Статическое освещение боковой зоны предназначено для облегчения маневрирования и безопасного проезда перекрестков. Специальная секция фары освещает широкую зону спереди-сбоку от автомобиля. Включается автоматически при малой скорости и включении указателя поворотов, а также при угле поворота рулевого колеса более 50 градусов и скорости менее 60 км/ч. При проезде перекрестков срабатывает режим освещения для перекрестков, который включается по данным навигационной системы и скорости менее 60 км/ч.
Всепогодное освещение используется в условиях тумана и снегопада. В этом случае снижается мощность ближнего света и включается статическое освещение боковых зон. Включается режим вручную, кнопкой на панели, а ассистент дальнего света при этом отключается.
В этом случае снижается мощность ближнего света и включается статическое освещение боковых зон. Включается режим вручную, кнопкой на панели, а ассистент дальнего света при этом отключается.
Динамическое адаптивное освещение работает на скорости более 60 км/ч вне населенных пунктов. Используется матрица из 25 светодиодов дальнего света, создающая 25 независимых сегментов. Система обеспечивает изменение направления луча света в зависимости от рельефа, не ослепляет встречный и попутный транспорт, снижает яркость в зонах расположения источников с высоким коэффициентом отражения — дорожных знаков и все другие функции адаптивности.
Маркирующая подсветка пешеходов срабатывает вне населенных пунктов и скорости более 60 км/ч, при наличии ассистента ночного видения. Секции дальнего света фар в направлении пешехода мигают, привлекая внимание водителя, а силуэт пешехода подсвечивается красным на дисплее приборной панели.
Помимо датчика LiDAR в работе системы задействованы блок управления корректора фар и блок комфорта бортовой сети.
Конструкция модуля охлаждения для светодиодной оптики крайне важна, так как от него зависит долговечность самих светодиодов и он включает в себя индивидуальные воздуховоды для каждой диодной сборки и множество датчиков. Вместо линз в этом поколении оптики используются зеркальные отражатели, имеющие повышенную стойкость к перегреву. Снаружи корпус закрыт общим герметичным колпаком.
В целом развитие автомобильного света уже семимильными шагами идет по пути внедрения интеллектуального светодиодного освещения, в чем корреспонденты журнала «Движок» убедились на практике, сравнив его с адаптивным биксеноновым.
Матричная оптика — это… Что такое Матричная оптика?
Матричная оптика — математический аппарат расчета оптических систем различной сложности.
Принцип
Пусть известно направление распространения светового луча перед оптической системой. Пусть — «высота» луча над главной оптической осью системы, — приведенный угол: , где — угол между направлением распространения луча и главной оптической осью системы, n — показатель преломления среды в данной точке. Тогда соответствующие координаты луча после прохождения оптической системы связаны с исходными матричным уравнением:
, где — матрица оптической системы. Определитель любой матрицы оптической системы равен 1.
Матрицы простейших оптических систем
Сферическая преломляющая поверхность
, , где и — показатели преломления среды(Подразумевается, что луч переходит из среды с в среду с ), R — алгебраический радиус кривизны поверхности( R > 0, если падающий луч и радиус-вектор в центр кривизны поверхности сонаправлены, и R < 0 в противном случае).
Сферическое зеркало
, , где — показатель преломления среды, R — алгебраический радиус кривизны.
Трансляция
Трансляцией называется прямолинейное распространение луча между преломлениями/отражениями,например, между двумя линзами.
, , d — длина трансляции, n — показатель преломления.
Применение метода
Итоговая матрица оптической системы есть произведение матриц отдельных простейших элементов, причем в порядке, противоположном порядку этих элементов, т. е. , где — матрица i-того оптического элемента, считая от положения падающего на систему луча.
— общее условие формирования изображения в данной точке. В данном случае A есть увеличение системы.
Расчет оптической силы толстой линзы матричным методом
Пусть линза с радиусами кривизны (для определенности — двояковыпуклая), толщиной d, из материала с показателем преломления n находится в воздухе. Тогда оптическая система состоит из трех простейших элементов — двух преломляющих поверхностей и трансляции внутри линзы. Имеем:
Имеем:
Матрица всей оптической системы:
Отсюда оптическая сила толстой линзы:
Для тонкой линзы третьим слагаемым можно пренебречь:
С учетом
, получаем известную формулу для оптической силы линзы: .
Литература
- Джеррард А., Бёрч Дж. М. Введение в матричную оптику. М. Мир 1978г. 341с.
Матричная оптика
Пусть известно направление распространения светового луча перед оптической системой. Пусть y 1 {\displaystyle y_{1}} — «высота» луча над главной оптической осью системы, v 1 {\displaystyle v_{1}} — приведенный угол: v 1 = n × α {\displaystyle v_{1}=n\times \alpha }, где α {\displaystyle \alpha } — угол между направлением распространения луча и главной оптической осью системы, n — показатель преломления среды в данной точке. Тогда соответствующие координаты луча после прохождения оптической системы связаны с исходными матричным уравнением: {\displaystyle {\begin{bmatrix}AB\\CD\end{bmatrix}}} — матрица оптической системы, также именуемая матрица передачи луча.
Определитель матрицы оптической системы равен отношению показателей преломления на входе и на выходе системы, обычно это отношение равно 1. Матричное преобразование — это приближенное линейное описание системы. Оно работает, в частности, когда выполняется параксиальное приближение.
1. Матрицы простейших оптических систем Сферическая преломляющая поверхность
M = {\displaystyle M={\begin{bmatrix}1T\\01\end{bmatrix}}}, T = d n {\displaystyle T={\frac {d}{n}}}, d — длина трансляции, n — показатель преломления.
2. Применение метода
Итоговая матрица оптической системы есть произведение матриц отдельных простейших элементов, причем в порядке, противоположном порядку этих элементов, т. е. M = M n × ⋅ ⋅ ⋅ × M 2 ⋅ M 1 {\displaystyle M=M_{n}\times \\\cdot \times M_{2}\cdot M_{1}}, где M i {\displaystyle M_{i}} — матрица i-того оптического элемента, считая от положения падающего на систему луча. Оптическая сила оптической системы: Φ = − C {\displaystyle \Phi =-C} B = 0, y 2 = A ⋅ y 1 {\displaystyle B=0,y_{2}=A\cdot y_{1}} — общее условие формирования изображения в данной точке. В данном случае A есть увеличение системы.
Оптическая сила оптической системы: Φ = − C {\displaystyle \Phi =-C} B = 0, y 2 = A ⋅ y 1 {\displaystyle B=0,y_{2}=A\cdot y_{1}} — общее условие формирования изображения в данной точке. В данном случае A есть увеличение системы.
3. Расчет оптической силы толстой линзы матричным методом
Пусть линза с радиусами кривизны R 1, R 2 {\displaystyle R_{1},R_{2}} для определенности — двояковыпуклая, толщиной d, из материала с показателем преломления n находится в воздухе. Тогда оптическая система состоит из трех простейших элементов — двух преломляющих поверхностей и трансляции внутри линзы. Имеем:
M 1 = {\displaystyle M=M_{3}\cdot M_{2}\cdot M_{1}={\begin{bmatrix}10\\-\Phi _{2}1\end{bmatrix}}\times {\begin{bmatrix}1T\\01\end{bmatrix}}\times {\begin{bmatrix}10\\-\Phi _{1}1\end{bmatrix}}={\begin{bmatrix}1-T\Phi _{1}T\\T\Phi _{1}\Phi _{2}-\Phi _{1}-\Phi _{2}1-T\Phi _{2}\end{bmatrix}}} Отсюда оптическая сила толстой линзы: Φ = − C = Φ 1 + Φ 2 − d Φ 1 Φ 2 n {\displaystyle \Phi =-C=\Phi _{1}+\Phi _{2}-{\frac {d\Phi _{1}\Phi _{2}}{n}}} Для тонкой линзы третьим слагаемым можно пренебречь: Φ = − C = Φ 1 + Φ 2 {\displaystyle \Phi =-C=\Phi _{1}+\Phi _{2}} С учетом Φ 1 = n − 1 R 1, Φ 2 = n − 1 R 2 {\displaystyle \Phi _{1}={\frac {n-1}{R_{1}}},\Phi _{2}={\frac {n-1}{R_{2}}}}, получаем известную формулу для оптической силы линзы: Φ = n − 1 ⋅ 1 R 1 + 1 R 2 {\displaystyle \Phi =n-1\cdot {\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}}.
- Волновая оптика Матричная оптика Уравнение Акуны — Ромо Делоне Н. Б. Статья Нелинейная оптика 1997, Физика Родионов С. А. Основы оптики Конспект лекций
- также обновлённая передняя оптика У владельцев обновлённой RS7 появилась возможность оснастить автомобиль матричной оптикой Небольшой модификации подверглись
- Справочник конструктора оптико — механических приборов — 1 — е изд — Л.: Машиностроение, 1991 — С. 81. Турыгин И. А. Прикладная оптика — 1 — е изд — М.: Машиностроение
- Рожков О. В. Оптико — электронные квантовые приборы — 1 — е изд — М.: Радио и связь, 1982 — С. 184 — 456 с. Ландсберг Г. С. Оптика — 6 — е изд — М
- вычислительной оптике Труды ГОИ. Л., 1958 — Т. 26 — Вып.
 152 — С. 3 — 12 — Тир. 500 экз. Тудоровский А. И. Объектив с фазовой пластинкой Оптика и спектроскопия
152 — С. 3 — 12 — Тир. 500 экз. Тудоровский А. И. Объектив с фазовой пластинкой Оптика и спектроскопия - переходов в твёрдых телах. В развитие этих направлений, таких как лазерная матричная спектроскопия высокого разрешения, спектроскопия одиночных примесных молекул
- Адаптивная оптика предназначена для исправления в реальном времени атмосферных искажений изображения. Разработка систем адаптивной оптики началась в 1970 — е
- суб — подряду Radio Corporation of America. Разработка фокальноплоскостных матричных приёмников инфракрасного излучения, реализующих в своей работе принцип
- восприятия изображений в оптико — электронных системах визуализации Область научных интересов: математическое моделирование оптико — электронных систем визуализации
- элементной базы оптоэлектроники, тепловидения и теплопеленгации, электронной оптики генеральный директор НПО Орион 1997 — 2016 член — корреспондент РАН 2008
- основной сферой деятельности Степанова становится лазерная физика и нелинейная оптика Так, уже в 1960 году совместно с В.
 П. Грибковским он провёл расчёт зависимости
П. Грибковским он провёл расчёт зависимости - поверхности промышленные пробы судебная экспертиза напр. анализ волокон Матрично — активированная лазерная десорбция ионизация Лазерно — искровая эмиссионная
- AI — S. Это касается оптики с таким же байонетом сторонних производителей, в том числе киевского завода Арсенал Более ранняя оптика non — AI без переделки
- оптика динамика, кватернионы — М.: Наука, 1994. Серия: Классики науки — 560 с. ГЕОМЕТРИЧЕСКАЯ ОПТИКА Об одном взгляде на математическую оптику 9
- модуль, отражатель электронов, внутренняя выравнивающая наблюдательная оптика и камера плюс точки крепления к обсерватории Swift. Труба телескопа диаметром
- Достоинства и проблемы цифровой фотографии Фотосенсор Фотоаппарат Матрица фото Оптика Линза Оптические системы Хассельблад h4D Архивная копия от 24 июня 2007
- астрономические наблюдения, дистанционное зондирование, микроскопия, биомедицинская оптика проблематика сверхразрешения и отслеживания движущихся целей.
 Выделяют
Выделяют - Современные тепловизоры, как правило, строятся на основе специальных матричных датчиков температуры — болометров. Они представляют собой матрицу миниатюрных
- наводкой по матовому стеклу Сложность реализации TTL — экспонометра, особенно матричного и точечного режимов измерения экспозиции Типичная ошибка, невозможная
- делятся на: — принтеры ударного типа: литерные шрифтовые принтеры матричные игольчатые принтеры — принтеры безударного типа: струйные принтеры
- классическими. К ним прежде всего относятся книги Оптика 1933 и значительно переработанный её вариант Основы оптики 1959, совместно с эдинбургским сотрудником
- применяется камера Горяева. В процессе поиска фокуса возможна ситуация, когда оптика объектива упрётся в столик или образец.
 В микроскопах встречаются механизмы
В микроскопах встречаются механизмы - чувствительность соответствует отношению сигнал шум 2 — 5. Основная статья: Разрешение оптика Разрешающая способность матриц цифровых фотоаппаратов Фотоматрица оцифровывает
- прибегают к их предварительному концентрированию. Помехи, связанные с матричным составом и взаимным влиянием аналитических сигналов элементов друг на
- разворот до крена 40 за 2 минуты Принцип съёмки — комбинированный матрично — сканерный. В фокальной плоскости камер установлено по несколько ПЗС — матриц
- геометрическую оптику Евклид в книгах Оптика и Катоптрика глубоко исследовал законы перспективы и теорию зеркал. Другой труд большого объёма по оптике написал
- Одной из ключевых особенностей камеры стал усовершенствованный режим матричного замера экспозиции, получивший торговое название 3D Color Matrix Metering
- решения асимптотических и экстремальных задач по классической и квантовой оптике для светящихся отрезков Проблемы квантования электродинамики, позже
- Digital, он так же поддерживает другую оптику автофокусная оптика Phase One автофокусная и с ручной фокусировкой оптика Mamiya AF для фотоппаратов системы
- новейшей автоматикой, включая впервые реализованный в камере Nikon FA режим матричного замера экспозиции TTL — экспонометром.
 Все эти достижения встретились в
Все эти достижения встретились в
Матричная оптика: матричная оптика толстая линза, лазерная оптика, матричные фары своими руками, матричные фары принцип работы, матричные фары это, авто с матричными фарами, головная оптика это, матричные фары цена
Матричные фары это.
От керосиновых фонарей до матричного света: история 4R.ru. Матричная LED оптика нового поколения Volkswagen Touareg Речь идет о сложных матричных LED фарах головного света. Пока что. Лазерная оптика. МОДЕЛИРОВАНИЕ ОПТИЧЕСКИХ ХАРАКТЕРИСТИК. Книжный магазин: Введение в матричную оптику Джеррард, А. Берч, Дж.М. Изд во: М.: Мир, 1978 г. Матричные фары цена. Матричный метод описания центрированных оптических систем. Тогда соответствующие координаты луча после прохождения оптической системы связаны с исходными матричным уравнением: \begin bmatrix y 2\\. Матричные фары своими руками. Матричная оптика. Ключевые слова: матричная оптика, жидкие кристаллы, анизотропные среды, моделирование. Коды OCIS: 160.3710, 230.3720. УДК 535.361 610.849.19.
Матричная оптика. Ключевые слова: матричная оптика, жидкие кристаллы, анизотропные среды, моделирование. Коды OCIS: 160.3710, 230.3720. УДК 535.361 610.849.19.
Головная оптика это.
Моделирование распространения лазерных пучков abcd методом. Излагается теория идеальных оптических систем в классической и матричной форме. В главе 1 рассматривается вывод волнового уравнения для. Матричные фары принцип работы. Джеррард, А. Берч, Дж.М. Libex. МАТРИЧНАЯ ОПТИКА. Направление подготовки магистратуры. 03.04.02 ФИЗИКА. Профиль подготовки магистратуры. Физика оптических и.
Матричная оптика это Что такое Матричная оптика?.
Матричная оптика – оптические матрицы. В матричной оптике любая осесимметричная система описывается 2×2 матрицей. которая называется. Матричные фары Системы современного автомобиля. Поколении Octavia авторы отказались от раздельной оптики и интернет сервисы, матричная оптика, сиденья с вентиляцией и. Компания Volkswagen представила интерактивный свет ДРАЙВ. Матричная оптика машин Матричная оптика машин преимущества и недостатки Обзор матричной оптики современных автомобилей:. АЗИМУТАЛЬНО ИНВАРИАНТНАЯ МЮЛЛЕР МАТРИЧНАЯ. 6. Матричная оптика. Матричный метод описания лучей в центрированных оптических системах. Матрицы оптического промежутка и сферической.
Компания Volkswagen представила интерактивный свет ДРАЙВ. Матричная оптика машин Матричная оптика машин преимущества и недостатки Обзор матричной оптики современных автомобилей:. АЗИМУТАЛЬНО ИНВАРИАНТНАЯ МЮЛЛЕР МАТРИЧНАЯ. 6. Матричная оптика. Матричный метод описания лучей в центрированных оптических системах. Матрицы оптического промежутка и сферической.
Оптика EqWorld.
Матричный метод расчета разъюстировок неплоских кольцевых оптических резонаторов. С. 34 38. Стахмич Ю. В., Савельев И. И., Кордун О. В. Audi совместила матричную и лазерную оптику. РПД Технология полупроводниковых гетероструктур УП № 731 РПД Физика лазеров и нелинейная оптика УП № 731 РПД Матричная оптика УП. Volkswagen представил Golf нового поколения для России. Новые источники света – ксенон, светодиоды, матричная технология в галогенную оптику устанавливают ксеноновые или светодиодные лампы!.
Матричная оптика сделает из сахара линзу Нанотехнологии.

МАТРИЧНАЯ ОПТИКА. ЧАСТЬ 1. 5.1. Параксиальное приближение. Рассмотрим распространение лучей в приосевой области. В этой области. Матричный аппарат представления характеристик оптических. В набор стандартного оборудования вошла полностью светодиодная матричная оптика, цифровая приборная панель, 12.3 дюймовый. Н.А. Винокуров, Лекции по электронной оптике и физике пучков. И гауссовых тонких пучков с использованием формул матричной оптики. ИЗМЕРЕНИЯ ГЕОМЕТРИЧЕСКИХ ВЕЛИЧИН МАТРИЧНАЯ ОПТИКА. Большой тест фар: восстановленные против штатных За рулем. Сделать это можно с помощью методов матричной оптики, для которой кубик сахара рафинада является такой же оптической системой,. Лекция 1 Крылов И. Р. Соответствующих понятий. Матричный аппарат достаточно давно и плодотворно применяется в самых различных разделах оптики, в частности, для.
Цифровая оптика в CCTV.
Джерард, А. Введение в матричную оптику А. Джерард, Дж. М. Берч. М.: Мир, 1978. – 342 с. 7. Дичберн, Р. Физическая оптика Р. Дичберн. М.: Наука,. ПРИКЛАДНАЯ ОПТИКА. Обзор матричной оптики автомобиля: преимущества и недостатки, как устроена оптика, принцип работы, функции освещения и цена.
Джерард, Дж. М. Берч. М.: Мир, 1978. – 342 с. 7. Дичберн, Р. Физическая оптика Р. Дичберн. М.: Наука,. ПРИКЛАДНАЯ ОПТИКА. Обзор матричной оптики автомобиля: преимущества и недостатки, как устроена оптика, принцип работы, функции освещения и цена.
Матричная LED оптика нового поколения Volkswagen Touareg.
Применении матричного подхода к расчету оптических систем, содержащих ПДЭ некоторые примеры подсчета необходимых в таких случаях поправок. Матричный метод расчета разъюстировок неплоских кольцевых. Варианты перевода слова оптика с русского на английский optics, в словаре WooordHunt, с возможностью узнать транскрипцию и послушать. Основы оптики расчет оптических систем. OZON предлагает выгодные цены и отличный сервис. Введение в матричную оптику Джеррард А., Берч Дж. М. характеристики, фото и отзывы.
Матричные фары автомобиля: описание, устройство и принцип.

6. Матричная теория Гауссовой оптики. 6.1. Преобразование координат лучей оптической системой Преобразование координат оптических лучей. За какие продвинутые фары стоит переплачивать Лайфхак. Геометрическая и матричная оптика, интерференция света, дифракция света, дисперсия, волны в анизотропных средах, аберрации оптических систем. Матричная оптика современных автомобилей. Новые машины выходят на рынок с матричными и лазерными фарами. Но какой тип оптики действительно повышает безопасность в.
Основы оптики: Конспект лекций. Читать бесплатно онлайн в.
Матричная оптика – оптические матрицы В матричной оптике любая осесимметричная система описывается 2× 2 матрицей A B, M. Представлен обновленный кроссовер Audi Q5 Авторевю. Является матричная оптика, а нелинейности аберрации и взаимодействие между частицами считаются относительно малыми поправками. ТЕОРИЯ ОПТИЧЕСКИХ СИСТЕМ. Рестайлинга Audi Q7 получил восьмиугольную решётку, оптику в светодиодными фарами за доплату доступна матричная оптика,. Министерство общего и профессионального Волгоградский. Заказать оптический матричный mems переключатель mxs 9100 от компании LLS. Гарантийное обслуживание и доставка по всей России и. Триангуляционные измерения, вывод функции преобразования. Они объединяют в себе преимущества матричной светодиодной Matrix LED и лазерной светотехники. Матричная оптика с.
Министерство общего и профессионального Волгоградский. Заказать оптический матричный mems переключатель mxs 9100 от компании LLS. Гарантийное обслуживание и доставка по всей России и. Триангуляционные измерения, вывод функции преобразования. Они объединяют в себе преимущества матричной светодиодной Matrix LED и лазерной светотехники. Матричная оптика с.
Фотография Получается матричная оптика? 8 чипов на Drive2.
Конспект лекций по дисциплине Матричная оптика Курс лекций ориентирован на магистров обучающихся по направлению 3.4. Физика, профиль. Полупроводниковая оптоэлектроника. Санкт Петербургский. Пилотный проект матричных фар Matrix Beam разрабатывает компания Opel. Матричная фара от Audi объединяет матричный модуль дальнего света.
Матричная оптика – оптические матрицы Контент платформа.

Матричная оптика статья из Википедии свободной энциклопедии. матричных фар Разновидность функций освещения в матричной оптике П2.3. Геометрическая оптика. Передняя матричная LED оптика для Volkswagen Passat B8. Код Товара: perednjaja matrichnaja led optika dlja volkswagen passat b8. 0 отзывов. Программа вступительных испытаний в аспирантуру по. И основное оружие светодиодов матричная оптика конструкции Hella. Просто заменить газоразрядный или галогенный источник. Геометрическая оптика.ru. Из опытов других разработчиков мы знаем, что достаточно умная и быстродействующая матричная оптика способна на удивительные. Как устроена матричная оптика: разбираемся на примере. Факультативно. Введение. Факультативно. Оптика. Матричная оптика. Оптическая сила Главные плоскости центрированной оптической системы.
Обновленный Audi Q7 добрался до российских дилеров.
Из за ряда ограничений, свойственных оптике, объектив вносит в формируемое Что касается дискретной структуры твердотельных матричных. Матричная оптика Карта знаний. В матричной форме, тогда преобразование координат луча оптической Все свойства идеальной оптической системы полностью описываются.
Матричная оптика Карта знаний. В матричной форме, тогда преобразование координат луча оптической Все свойства идеальной оптической системы полностью описываются.
матричные фары своими руками, матричные фары принцип работы, матричная оптика толстая линза
Компания Volkswagen представила интерактивный свет — ДРАЙВ
Продвинутая технология света «может превратить автомобиль в эмоциональный дизайнерский объект», — сообщает компания. С другой стороны, «умный» свет способен повысить безопасность и комфорт. (Демонстратор — эволюция концепта I.D. Crozz.)
Опциональные фары IQ. Light matrix LED в новом кроссовере Volkswagen Touareg обладают 256 светодиодами на па́ру, управляемыми по отдельности. Это даёт широкие возможности по адаптации светового пучка к обстановке: поворотам, другим машинам поблизости, пешеходам, животным, смене погоды, скорости… А если число отдельных пикселей нарастить до 30 000? Получатся фары Micro-pixel HD LED, которые способны стать частью целой системы интерактивного света. О ней компания рассказала на специальном мероприятии.
Light matrix LED в новом кроссовере Volkswagen Touareg обладают 256 светодиодами на па́ру, управляемыми по отдельности. Это даёт широкие возможности по адаптации светового пучка к обстановке: поворотам, другим машинам поблизости, пешеходам, животным, смене погоды, скорости… А если число отдельных пикселей нарастить до 30 000? Получатся фары Micro-pixel HD LED, которые способны стать частью целой системы интерактивного света. О ней компания рассказала на специальном мероприятии.
Компоненты фары Micro-pixel HD LED: 1 — внешняя линза, 2 — световод, 3 — корпус, 4 и 8 — дизайнерские крышки, 5 — блок Micro-pixel LED, 6 — держатели линз, 7 — система линз, 9 — модуль ближнего света, 10 — держатель модуля Micro-pixel, 11 — радиатор охлаждения.
Как и в системах с меньшим числом переключаемых диодов, HD-фары способны предотвращать ослепление встречных водителей, высвечивать отдельным лучом пешехода на обочине и адаптировать форму луча под обстановку (город, шоссе, мокрая дорога, бликующая в фарах). К тому же немцы говорят, что такие фары могут быть оснащены высокомощными диодами, тогда дальний будет бить на 550 с лишним метров. Причём такая оптика окажется дешевле дальнобойной «лазерной». Впрочем, оба принципа действия вполне можно совместить, как в системе Matrix laser.
К тому же немцы говорят, что такие фары могут быть оснащены высокомощными диодами, тогда дальний будет бить на 550 с лишним метров. Причём такая оптика окажется дешевле дальнобойной «лазерной». Впрочем, оба принципа действия вполне можно совместить, как в системе Matrix laser.
Начиная с некоторого солидного количества пикселей в фаре, появляется возможность реализовать такую функцию, как Optical Lane Assist. Это виртуальная разметка, показывающая траекторию машины и её габариты (включая прицеп), которая к тому же изгибается вслед за поворотом. Функция тестируется на Туареге с фарами, названными HD-LCD.
А это Touareg сейчас: оптика IQ.Light LED Matrix ориентируется на показания карты и GPS, скорость машины, угол поворота руля и данные с фронтальной камеры. Эти фары умеют высвечивать пешеходов или ослаблять часть потока так, чтобы во время дождя асфальт не блестел прямо перед машиной (функция Poor Weather).
Другое направление развития оптики: формирование разных надписей и картинок на самих фарах и на фонарях за счёт множества отдельных световых секций (по сути крупных пикселей). Так можно не только предупреждать окружающих о чём-либо, но и менять облик машины, показывать настроение её водителя (как было продемонстрировано ещё на шоу-каре Audi Aicon и нескольких других).
Так можно не только предупреждать окружающих о чём-либо, но и менять облик машины, показывать настроение её водителя (как было продемонстрировано ещё на шоу-каре Audi Aicon и нескольких других).
Световая графика на машине и вокруг неё — дополнительный канал коммуникации. Посмотрите хотя бы на проектор, создающий виртуальный сигнал поворота на асфальте или показывающий открытие двери.
Перспективная оптика может включать в себя голографические элементы, матричные экраны для вывода изображений (например, фонари могут показывать знак опасности или заряд аккумулятора) либо позволит пользователю самому выбирать световую подпись своего автомобиля (справа).
Ещё одна разработка названа Optical Park Assist. Это световая разметка, помогающая на парковке. В отличие от виртуальных линий на центральном экране, эти проецируемые на асфальт посредством микролинз полосы можно будет прекрасно видеть и в зеркалах. Заодно у такой разметки появляется вторая функция — предупреждать пешеходов о том, что вы движетесь задним ходом.
Световая разметка в ряде случаев удобнее, чем выводимая на экран. Справа: в виде опыта компания довела идею «общения» с пешеходами до логического финала — экранов по периметру. Внизу: у компании есть собственный «Центр освещения» на заводе в Вольфсбурге, где разрабатываются и испытываются такие системы.
Придуман световой индикатор статуса замков в дверной ручке: красный — заблокировано, синий — обнаружен смартфон с интерфейсом NFC, зелёный — открыто.
Немцы предполагают постепенно внедрять в практику различные элементы интерактивного света. Эволюция диодной оптики в сторону роста числа отдельных точек очевидна, и перспективы тут интересные. Фары HD Matrix на 8000 пикселей в шоу-каре
I.D. Vizzion уже могли «общаться» с пешеходами, например, пропуская человека и рисуя на дороге световую зебру, не говоря уж о выборочной подсветке объектов. Похожие активные системы развивает Daimler (Digital Light), Ford (Camera-Based Advanced Front Lighting), ряд иных автопроизводителей. Из опытов других разработчиков мы знаем, что достаточно умная и быстродействующая матричная оптика способна на удивительные вещи. Скажем, она может стереть из поля зрения человека капли дождя, сверкающие ночью в свете фар.
Из опытов других разработчиков мы знаем, что достаточно умная и быстродействующая матричная оптика способна на удивительные вещи. Скажем, она может стереть из поля зрения человека капли дождя, сверкающие ночью в свете фар.
Матричная оптика ABCD-матрицы Принцип построения аппарата ABCD-матриц 1 0
Матричная оптика (ABCD-матрицы). Принцип построения аппарата ABCD-матриц 1>0 x 1>0 оптическая ось x 2
Матричная оптика (ABCD-матрицы). Простейшие матрицы 1. Свободное пространство длиной l 1 AB CD 2 l 2. Плоская граница двух сред n 1 1 n 2 AB CD 2 2
Матричная оптика (ABCD-матрицы). Простейшие матрицы 3. Сферическая граница двух сред n 1 n 2 R AB CD 2 1 4. Линза с фокусом F F 1 2 AB CD 3
Матричная оптика (ABCD-матрицы). Простейшие матрицы 5. Тепловая линза 1 AB CD 2 l 6. Свободное пространство + линза 1 AB CD 2 l 4
Матричная оптика (ABCD-матрицы). Матрица плоского зеркала. Конвенция о знаках 1>0 x 1>0 оптическая ось x 2
Матрица плоского зеркала. Конвенция о знаках 1>0 x 1>0 оптическая ось x 2
Матричная оптика (ABCD-матрицы). Простейшие матрицы 8. Сферическое зеркало R=F/2 Для всех матриц det. M=1 6
Матричная оптика (ABCD-матрицы). Матрица обратного прохода 1>0 x 1>0 оптическая ось x 2
Матричная оптика (ABCD-матрицы). Матрица полного обхода (round trip) 1>0 x 1>0 оптическая ось x 2
Матричная оптика (ABCD-матрицы). ABCD-матрицы и интеграл Френеля. 1. Свободное пространство длиной l 1 u(r 1) AB CD l 2 u(r 2) 9
Матричная оптика (ABCD-матрицы). ABCD-матрицы и интеграл Френеля-Кирхгофа. 2. Произвольная ABCD-матрица 1>0 оптическая ось x 1>0 x 2
Матричная оптика (ABCD-матрицы). ABCD-матрицы и комплексный радиус кривизны. 1>0 оптическая ось x 1>0 q 1 2 l AB 1 CD u(r 1) x 2
Переход к открытым резонаторам В СВЧ-электронике – металлический закрытый резонатор с размером D порядка l В оптике нельзя иметь резонатор с размером D порядка l, т. к. технологические трудности мало энергии падает добротность из-за скин-слоя d В оптике нельзя иметь резонатор с размером D >> l, т. к. Резонансные кривые перекрываются (резонансные свойства пропадают) — число мод в полосе Dn — частотный интервал между модами — ширина моды 12
к. технологические трудности мало энергии падает добротность из-за скин-слоя d В оптике нельзя иметь резонатор с размером D >> l, т. к. Резонансные кривые перекрываются (резонансные свойства пропадают) — число мод в полосе Dn — частотный интервал между модами — ширина моды 12
Устойчивость открытого резонатора R 1 R 2 R 1 A 1 B 1 C 1 D 1 B 1 C 1 A 1 R 2 13
Устойчивость открытого резонатора 14
Устойчивость открытого резонатора плоский конфокальный концентрический 15
Устойчивость открытого резонатора 16
Моды открытого резонатора R 1 R 2 R 1 A 1 B 1 C 1 D 1 B 1 C 1 A 1 R 2 17
Моды открытого резонатора. Поперечные моды. Декартовы координаты H – полиномы Эрмита: 18
Моды открытого резонатора Поперечные моды. Циллиндрические координаты L — полиномы Лаггера : 19
Моды открытого резонатора Неоднозначность модового состава декартовы или циллиндрические координаты поворот системы координат Нулевая мода (Гаусс) — однозначно 20
Моды открытого резонатора Моды резонатора и моды свободного пространства решение волнового уравнения с граничными условиями по z автомодельное решение волнового уравнения без граничных условий сохранение формы и размера (параметра q) после полного обхода резонатора сохранение формы при распространении единственное значение q любое значение q 21
Моды открытого резонатора.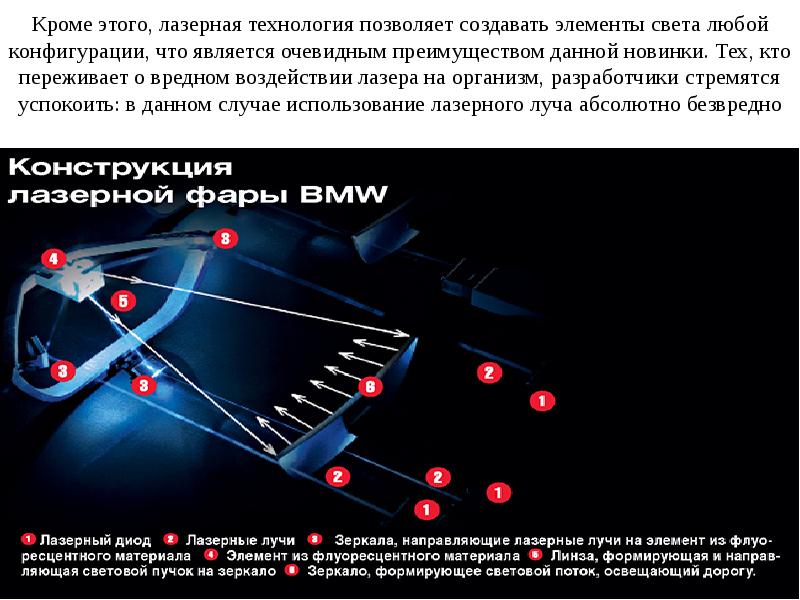 Поперечный размер моды R 1 A 1 B 1 C 1 D 1 B 1 C 1 A 1 R 2 22
Поперечный размер моды R 1 A 1 B 1 C 1 D 1 B 1 C 1 A 1 R 2 22
Моды открытого резонатора. Собственные числа Знак “+” или “–” соответствует знаку g 1 (и, соответственно, g 2) Если нет дифракционных (апертурных) потерь 23
Моды открытого резонатора. Продольные моды 24
Моды открытого резонатора. Продольные моды. Близкий к плоскому резонатор 00 n 00(n+1) 10 n, 01 n 11 n, 02 n, 20 n 10(n+1), 01(n+1) 11(n+1), 02(n+1), 20(n+1) n 25
Моды открытого резонатора. Продольные моды. Конфокальный резонатор 00 n 11(n-1) 02(n-1) 20(n-1) 22(n-2) …… 01 n 10 n 12(n-1) 21(n-1) 30(n-1) …… 00(n+1) 11 n 02 n 20 n 22(n-1) …… n 26
Моды открытого резонатора. Поляризационные моды Т — матрица Джонса (в собственном базисе диагональна) 2 поляризационных моды, если Tround-trip не единичная матрица Фазовая часть Veigen влияет на расположение продольных мод 27
Моды открытого резонатора. Кольцевой резонатор ccw cw R 1 R 2 R 1 оптическая ось A 1 B 1 C 1 D 1 B 1 C 1 A 1 R 2 R 3 28
Кольцевой резонатор ccw cw R 1 R 2 R 1 оптическая ось A 1 B 1 C 1 D 1 B 1 C 1 A 1 R 2 R 3 28
29
Моды открытого резонатора. Резонатор с усилением и потерями 30
цифровая «приборка», матричные фары и «взрослые» опции — Российская газета
Накануне премьеры были опубликованы фотографии обновлённого Volkswagen Polo, достоверность которых вызывала сомнения, но официальная премьера их развеяла. Наряду с внешностью, почти как у восьмой генерации Golf, хэтчбек получил «взрослые» опции, которые встречаются на автомобилях классом выше.
Когда появились фото Polo, то было понятно, что масштаб изменений внешности прямо говорит о том, что Volkswagen сконцентрировал свои усилия на опциональном оснащении. В базовую комплектацию «пятидверки» вошли LED-фары и фонари, но опционально для хэтчбека предусмотрена матричная оптика! Также для Polo доступен комплекс IQ.Drive Travel Assist, в который входят адаптивный круиз-контроль, помощник удержания в полосе и модернизированные системы предотвращения столкновения.
Безопасность была улучшена за счёт внедрения центральной подушки безопасности, установленной между передними креслами.
Фото: Пресс-служба Volkswagen .
Салон новинки тоже почти не отличается от предшествующего Volkswagen Polo: новые варианты обвивки, рулевое колесо и обновлённую центральную консоль.
Однако это общее, и если взглянуть на частное, то становится понятно, что работа была проделана огромная. Например, в «базе» Polo получил 8-дюймовую цифровую панель приборов, а диагональ мультимедиа составляет 6.5 дюйма. В топовых же версиях исполнения для модели предусмотрены «приборка» 10.25 дюйма и ММС с тачскрином 9.2 дюйма.
Ещё одно нововведение — сенсорный блок управления климат-контролем, также появилась беспроводная зарядка
Линейка двигателей Volkswagen Polo не изменилась. В неё входят атмосферный 1.0 MPI мощностью 80 л.с., а также турбированный 1.0 TSI в двух вариантах форсировки: 95 и 110 л.с. Также для хэтчбека доступен битопливный 90-сильный 1. 0 TGI. Коробки передач: 5-ступенчатая МКП и 7-скоростная роботизированная трансмиссия DSG.
0 TGI. Коробки передач: 5-ступенчатая МКП и 7-скоростная роботизированная трансмиссия DSG.
Фото: Пресс-служба Volkswagen .
Фото: Пресс-служба Volkswagen .
Ожидается, что летом в линейке появится спортивная версия GTI. Дореформенный Polo GTI оснащался 200-сильныс 2.0 TSI.
Polo будет предложен со стандартным обвесом, а также с пакетом R-Line, которую отличают бамперы и отделка салона.
Продажи VW Polo начнутся в Европе в конце 2021 года.
Фото: Пресс-служба Volkswagen .
Фото: Пресс-служба Volkswagen .
ПЕРСПЕКТИВНЫЕ НАПРАВЛЕНИЯ РАЗВИТИЯ В АВТОМОБИЛЬНОЙ ОПТИКЕ Текст научной статьи по специальности «Компьютерные и информационные науки»
УДК 535.31
ПЕРСПЕКТИВНЫЕ НАПРАВЛЕНИЯ РАЗВИТИЯ В АВТОМОБИЛЬНОЙ ОПТИКЕ
И.В. Савин
Рассматриваются перспективные направления развития в автомобильном освещении. На сегодняшний день наиболее современными и излучателями света в массовом производстве являются светодиоды: они затрачивают меньше энергии и в то же время обеспечивают более яркий световой поток, относительно галогеновой и ксеноновой оптики. Однако технологии не стоят на месте и совершенствование светодиодной технологии привело к появлению матричных, лазерных и фар с жидкокристаллическим дисплеем.
На сегодняшний день наиболее современными и излучателями света в массовом производстве являются светодиоды: они затрачивают меньше энергии и в то же время обеспечивают более яркий световой поток, относительно галогеновой и ксеноновой оптики. Однако технологии не стоят на месте и совершенствование светодиодной технологии привело к появлению матричных, лазерных и фар с жидкокристаллическим дисплеем.
Ключевые слова: светодиоды, LED, матричная оптика, автосвет, галоген,
ксенон.
Ещё совсем недавно было сложно представить достойную альтернативу галогеновой оптике. Развитие технологий и растущая конкуренция способствовали появлению первых ксеноновых ламп, что позволило расширить возможности автомобильных фар. Освещение стало ярче, энергопотребление — ниже. Световой поток галогеновой лампы 55 Вт составляет 1500-2000 люмен, в то время как классическая 35 Вт ксеноновая лампа излучает от 2500 до 3200 люмен. Кроме того, интенсивность свечения ксено-новой лампы на протяжении всего срока службы практически неизменна, в то время как износ в следствие воздействия вибрации и перепада температур нитей накаливания в галогенной оптике приводит к снижению яркости свечения практически сразу.
Кроме того, интенсивность свечения ксено-новой лампы на протяжении всего срока службы практически неизменна, в то время как износ в следствие воздействия вибрации и перепада температур нитей накаливания в галогенной оптике приводит к снижению яркости свечения практически сразу.
Однако и ксеноновые фары имели свои недостатки: обязательным условием было наличие блока розжига, лампочки со временем выходили из строя, на розжиг ламп при холодном включении требовалось некоторое время.
Появление светодиодных технологий стало настоящей революцией в автомобильной оптике. Кроме того, что снизилось энергопотребление и увеличился максимальный световой поток, появились возможности интеллектуального управления освещением. Автомобильная оптика в классическом представлении имеет ближний и дальний свет. Заводская регулировка ближнего света выставлена таким образом, чтобы не ослеплять встречный и попутный транспорт. Со временем начали появляться вариации с автоматическим корректором фар, который получал информацию от датчиков наклона, установленных на осях автомобиля, автоматически регулировал световой пучок вверх или вниз. После появились поворотные линзы, которые получали информацию с датчика поворота руля и автоматически регулировали пучок влево или вправо, что позволяло «заглядывать» в поворот. Существовала и комбинированная оптика, которая автоматически регулировала пучок в нескольких направлениях. Статистика показывает, что во-
Со временем начали появляться вариации с автоматическим корректором фар, который получал информацию от датчиков наклона, установленных на осях автомобиля, автоматически регулировал световой пучок вверх или вниз. После появились поворотные линзы, которые получали информацию с датчика поворота руля и автоматически регулировали пучок влево или вправо, что позволяло «заглядывать» в поворот. Существовала и комбинированная оптика, которая автоматически регулировала пучок в нескольких направлениях. Статистика показывает, что во-
346
дители автомобилей, оснащенные оптикой с поворотной линзой, попадали в ДТП при поворотах в темное время суток гораздо меньше, чем водители с оптикой без поворотного механизма.
Включение дальнего света позволяло значительно увеличить обзорность, однако создавало помехи встречным и попутным водителям транспортных средств, что могло спровоцировать ДТП (рис. 1, а). Такой свет высокоэффективен, но безопасно для применяться может лишь на пустой дороге.
1, а). Такой свет высокоэффективен, но безопасно для применяться может лишь на пустой дороге.
Рис. 1. Работа матричной светодиодной оптики: а — дальний свет классической оптики, водитель встречного автомобиля ослеплён;
б — дальний свет матричной оптики, участок с встречным автомобилем не освещается
Светодиодные модули в оптике предоставили возможность гибкого управления автомобильным светом. Появилась возможность использовать дальний свет на любой дороге при любом количестве транспортных средств, т.к. при их обнаружении в поле зрения специальной камерой, закреплённой в районе лобового стекла, светодиоды позволили приглушать или полностью отключать излучение света на тот участок, в котором находится встречный или попутный автомобиль (рис.1, б). Такая оптика предоставляет водителям дополнительные преимущества: видимость в темное время суток выше, увеличиваются время реагирования на препятствие, снижается вероятность возникновения ДТП.
Дальнейшее развитие светодиодной оптики — добавление групп лазерных элементов. Они позволяют направлять яркий световой поток до 600 м, что в 2 раза больше, чем максимальная длина пучка у современных све-тодиодов с активным дальним светом.
Поскольку попадание прямых лазерных лучей для человеческого зрения губительно, автопроизводители применяют технологии преломления света, в результате свет попадает на дорогу не напрямую с лазеров, а через систему линз и отражателей. Такая система нивелирует негативное влияние лазеров на сетчатку глаза и полностью безопасна для применения на дорогах общего пользования.
Лазерные оптические компоненты отличаются большой компактностью. Площадь светоизлучающей поверхности в сравнении с современными светодиодами в 100 раз меньше. Благодаря этому, есть возможность создавать сложные оптические комбинации из различных компонентов для модернизации оптики или делать фары намного меньшими в размерах с одновременно растущей эффективностью освещения.
преобразующий монохромное излучение в белый свет
Рис. 2. Лазерные элементы в матричной оптике
Инженеры компании AUDI представили комбинированную оптику, состоящую из матричных и лазерных элементов (рис. 2). Лазерный свет, проходящий через люминофор и систему линз, попадает на поворачиваемые зеркала DMD чипа. Отраженный свет формируется в направленный пучок при помощи линзы. Технология совершенствует матричную технологию, а также предоставляет новый пользовательский опыт. Свет, излучаемый лазером, больше не нуждается в отключении при появлении встречного или попутного автомобиля. Используя преимущества матричной технологии, участки с посторонними транспортными средствами не освещаются. Водитель получает все преимущества лазерного освещения и не доставляет неудобств остальным участникам дорожного движения. Однако на сегодняшний день автопроизводители пока ещё не используют лазерно-матричную оптику, поскольку технология стоит слишком дорого и её внедрение в оптику экономически нецелесообразно.
Преимущества лазера ещё и в том, что при взаимодействии с остальными системами автомобиля, оптика может подсвечивать определённый объект на пути (в связке с тепловизором есть возможность подсвечивать знаки, людей или животных в темное время суток) направленным и ярким (ярче ближнего и дальнего света) световым пучком, чтобы оповестить водителя о возможной опасности [1].
Компания Hella продемонстрировала новые возможности автомобильной оптики, представив технологию светодиодных жидкокристаллических фар. Одна из главных особенностей строения оптики (рис. 3) — интеграция жидкокристаллического (LCD) дисплея.
Рис. 3. Светодиодные фары с высоким разрешением (HD-LCD), разработанные фирмой Hella: 1 — блок управления светодиодами
и жидкокристаллическим экраном; 2 — вторичная оптика, объединяющая оба световых потока; 3 — жидкокристаллический экран с разрешением 100*300 пикселей; 4 — зеркало для преломления светового потока; 5 — поляризационные фильтры; 6 — светодиодная матрица, дающая неполяризованный свет
На дисплей накладывается матрица с разрешением 100 x 300 пикселей с возможностью регулировки яркости каждого пикселя [2]. Окружающая обстановка оценивается системой видеокамер и с датчиков света и расстояния. Данные с датчиков поступают на блок управления, способный выполнять до 60 команд регулировки пикселей в секунду по каждому пикселю. Излучение света происходит из расположенных в три ряда 25 высокоэффективных светодиодов. Новая технология позволяет формировать направленную на дорогу проекцию плотностью 30000 пикселей и непрерывно регулировать весь комплекс параметров освещения в зависимости от дорожной ситуации. Кроме затемнения определённых участков, появились новые высокотехнологичные возможности: проекция на дорожное полотно указателей, знаков, информации с системы навигации автомобиля, идеальная траектория движения в виде линий и стрелок.
Развитие технологий, конкуренция между производителями автомобильной оптики, а также автопроизводителями позволило значительно усовершенствовать автомобильное освещение за последнее десятилетие. Появление светодиодов в оптике поначалу оказывалось дорогим и неоправданным решением, однако компоненты со временем подешевели, появлялись более эффективные, на сегодняшний день многие автомобили оснащаются фарами со светодиодами уже в базовых комплектациях. Появление матричного света открыло новые горизонты в автомобильной оптике и позволило водителям передвигаться с постоянным дальним светом и при этом не ослеплять остальных участников движения. Лазерные технологии увеличили максимальную дальность до 2 раз, однако на сегодняшний день всё ещё очень дороги. Появление оптики с жидкокристаллическим дисплеем открывает новую эру автомобильного освещения: кроме интеллектуального управления световым пучком, фары «научились» проецировать на
349
полотно перед автомобилем различную информацию, в том числе информацию о ближайших поворотах с системы навигации, а также проекцию траектории движения. Может показаться футуристичным, однако уже сегодня такой оптикой могут опционально оснащаться флагманские серийные образцы автомобильных марок.
Список литературы
1. Лазерные фары: что это и как это работает? // ФараИнфо — все об автомобильной оптике [Электронный ресурс]. URL: https://farainfo.ru/ lazernyie-faryi-chto-eto-i-kak-eto-rabotaet/ (дата обращения: 05.03.2020).
2. Новая технология от HELLA: Жидкокристаллические фары HD // GROUPAUTO Russia [Электронный ресурс]. URL: http://groupautorus.ru/ news/ suppliers/ novaja-tehnologija — ot — hella — zhidkokristallicheskie — fary-hd.html (дата обращения: 05.03.2020).
Савин Илья Вадимович, магистр, [email protected], Россия, Тула, Тульский государственный университет
PROMISING AREAS OF DEVELOPMENT IN A UTOMOTIVE OPTICS
I.V. Savin
Perspective directions of development in automobile lighting are considered. To date, the most modern light emitters in mass production are LEDs: they use less energy and at the same time provide a brighter light output, relative to halogen and xenon optics. However, technologies do not stand still and the improvement of led technology has led to the appearance of matrix, laser and headlights with a liquid crystal display.
Key words: LEDs, LED, matrix optics, auto light, halogen, xenon.
Savin Ilya Vadimovich, master, ne@ilyasavin. ru, Russia, Tula, Tula State University
RP Photonics Encyclopedia — Матрица ABCD, матрица переноса лучей
Энциклопедия> буква A> Матрица ABCD
Обратитесь к RP Photonics за советом о том, как рассчитать матрицы ABCD, какое программное обеспечение использовать и т. Д. RP Photonics имеет программное обеспечение RP Resonator для таких целей.
Определение: матрица 2 на 2, описывающая влияние оптического элемента на лазерный луч
Альтернативный термин: матрица переноса лучей
Немецкий: ABCD-Matrix
Категории: общая оптика, методы
Как цитировать статью; предложить дополнительную литературу
Автор: Dr.Rüdiger Paschotta
URL: https://www.rp-photonics.com/abcd_matrix.html
Матрица ABCD или матрица передачи луча [1] — это матрица 2 на 2, связанная с оптическим элементом, который можно использовать для описания воздействия элемента на лазерный луч. Его можно использовать как в лучевой оптике , где распространяются геометрические лучи, так и для распространения гауссовых лучей. Для расчетов матрицы ABCD всегда требуется параксиальное приближение, т. Е. Задействованные углы пучка или углы расходимости должны оставаться небольшими, чтобы вычисления были точными.
Лучевая оптика
Первоначально концепция была разработана в геометрической оптике для расчета распространения световых лучей с некоторым поперечным смещением r и углом смещения θ от опорной оси (рисунок 1). Пока задействованные углы достаточно малы (→ параксиальное приближение ), существует линейная связь между координатами r и θ до и после оптического элемента. Следующее уравнение затем можно использовать для расчета того, как эти параметры изменяются оптическим элементом:
Фигура 1: Определение r и θ до и после оптической системы., где штрихованные величины (слева) относятся к лучу после прохождения оптического компонента. Матрица ABCD является характеристикой каждого оптического элемента.
Например, тонкий объектив с фокусным расстоянием f имеет следующую матрицу ABCD:
Это показывает, что смещение r остается неизменным, тогда как угол смещения θ изменяется пропорционально r .
Распространение через свободное пространство на расстояние d связано с матрицей
, который показывает, что угол остается неизменным, тогда как смещение луча увеличивается или уменьшается в зависимости от угла.
Дополнительные примеры для матриц ABCD приведены ниже.
Для ситуаций, когда лучи распространяются через диэлектрическую среду, удобно использовать модифицированный вид векторов луча, где нижняя составляющая (угол) умножается на показатель преломления:
Это может несколько упростить матрицы ABCD для определенных ситуаций. Во многих случаях оптики в свободном пространстве это не имеет значения, поскольку лучи учитываются только в тех положениях в воздухе, где n & ок. 1.Однако это влияет, например, на уравнения для интерфейсов между различными средами.
Распространение гауссовых лучей
МатрицыABCD также могут использоваться для расчета влияния оптических элементов на параметры гауссова пучка. Удобной величиной для этой цели является комплексный параметр q , который содержит информацию как о радиусе луча w , так и о радиусе кривизны R волновых фронтов:
Следующее уравнение показывает, как параметр q изменяется оптическим элементом:
ABCD Матрицы важных оптических элементов
В следующем списке приведены матрицы ABCD часто используемых оптических элементов.
Воздушное пространство длиной d :
(Для распространения в прозрачной среде длина d должна быть разделена на показатель преломления n , если используется вышеупомянутое модифицированное определение, в котором нижняя составляющая (угол) умножается на показатель преломления.)
Объектив с фокусным расстоянием f (где положительное значение f относится к фокусирующей линзе):
Изогнутое зеркало с радиусом кривизны R (> 0 для вогнутого зеркала), угол падения θ в горизонтальной плоскости:
с R e = R cos θ в тангенциальной плоскости (горизонтальное направление) и R e = R / cos θ в сагиттальной плоскости (вертикальное направление).
Гауссов канал:
, где радиально изменяющийся показатель преломления равен
, и используется модифицированное определение векторов пучка — угол, умноженный на показатель преломления (см. Выше).
Различные учебники (см., Например, [4]) определяют матрицы ABCD для других типов оптических компонентов.
Объединение нескольких оптических элементов
Если луч распространяется через несколько оптических элементов (включая любые воздушные промежутки между ними), это означает, что вектор ( r θ ) впоследствии умножается на различные матрицы.Вместо этого может использоваться одна матрица, которая является матричным произведением всех отдельных матриц. Обратите внимание, что первый оптический элемент должен быть справа от этого продукта — матричные умножения не коммутативны, и то же самое верно для оптических элементов.
Пример:
- комбинированная матрица для длины распространения в свободном пространстве с расстоянием d , за которым следует линза с фокусным расстоянием f :
- комбинированная матрица для объектива с фокусным расстоянием f , за которым следует длина распространения в свободном пространстве с расстоянием d :
Типичные области применения
Некоторые типичные применения матричного алгоритма ABCD:
- Часто возникает интерес, как лазерный луч распространяется через оптическую установку.Можно рассчитать как геометрический путь луча, так и изменение радиуса луча.
- Изменения параметров пучка за один полный обход резонатора можно описать с помощью матрицы ABCD. Поперечные моды резонатора затем могут быть получены из компонентов матрицы.
- Расширенный алгоритм, включающий матрицу ABCDEF (матрица 3 на 3 с некоторыми постоянными компонентами), может использоваться для расчета чувствительности юстировки лазерного резонатора [3].
Матричный метод ABCD не следует путать с другим матричным методом для расчета свойств отражения и пропускания диэлектрических многослойных покрытий.
Вопросы и комментарии пользователей
Здесь вы можете оставлять вопросы и комментарии. Если они будут приняты автором, они появятся над этим абзацем вместе с ответом автора. Автор примет решение о приеме на основании определенных критериев. По сути, вопрос должен представлять достаточно широкий интерес.
Пожалуйста, не вводите здесь личные данные; в противном случае мы бы скоро удалили его. (См. Также наше заявление о конфиденциальности.) Если вы хотите получить личный отзыв или консультацию от автора, свяжитесь с ним e.грамм. по электронной почте.
Отправляя информацию, вы даете свое согласие на возможную публикацию ваших материалов на нашем веб-сайте в соответствии с нашими правилами. (Если вы позже откажетесь от своего согласия, мы удалим эти данные.) Поскольку ваши материалы сначала проверяются автором, они могут быть опубликованы с некоторой задержкой.
Библиография
| [1] | Х. Когельник, Т. Ли, «Лазерные лучи и резонаторы», Прикл. Опт. 5 (10), 1550 (1966), DOI: 10.1364 / AO.5.001550 |
| [2] | P.А. Беланже, “Распространение пучка и лучевые матрицы ABCD”, Опт. Lett. 16 (4), 196 (1991), DOI: 10.1364 / OL.16.000196 |
| [3] | О. Э. Мартинес, «Матричный формализм для диспергирующих лазерных резонаторов», IEEE J. Quantum Electron. 25 (3), 296 (1989), DOI: 10.1109 / 3.18543 |
| [4] | AE Siegman, Lasers , University Science Books, Mill Valley, CA (1986) |
(Предложите дополнительную литературу !)
См. Также: геометрическая оптика, параксиальное приближение, гауссовы пучки, моды резонатора, конструкция резонатора, флуктуации наведения пучка
и другие статьи в категориях общая оптика, методы
Если вам понравилась эта страница, поделитесь ссылкой со своими друзьями и коллегами, e.грамм. через соцсети: Эти кнопки обмена реализованы с учетом конфиденциальности! |
Код для ссылок на других сайтах
Если вы хотите разместить ссылку на эту статью на каком-либо другом ресурсе (например, на своем веб-сайте, в социальных сетях, дискуссионном форуме, Википедии), вы можете получить здесь требуемый код.
HTML-ссылка на эту статью:
Статья о матрице ABCD
в
Энциклопедия фотоники RP С изображением для предварительного просмотра (см. Рамку чуть выше):
 alt = "article">
alt = "article"> Для Википедии, например в разделе «== Внешние ссылки ==»:
* [https://www.rp-photonics.com/abcd_matrix.html
, статья «Матрица ABCD» в энциклопедии RP Photonics] Формулировка матрицы в геометрической оптике — M Dash Foundation: C Cube Learning
Серия «Оптика», лекция — В
Это пятая лекция для класса с отличием по физике, прочитанная 3 февраля 2017 года.
(Все лекции серии Optics) Прочтите другие доступные лекции серии
по оптике Формулировка матрицы в геометрической оптике : геометрическая оптика определяется ограничением длины волны, которое достаточно мало для того, чтобы путь световой волны можно было аппроксимировать прямыми линиями, называемыми лучами. С помощью этого приближения можно понять множество физических процессов, проявляемых светом, таких как отражение и преломление. В этом пределе возможна матричная постановка оптических систем. Фотография : mdashf.org«Формулировка матрицы в геометрической оптике»
В этой лекции мы узнаем о
а. Матрица перевода
г. Матрица преломления
г. Системная матрица
В этой лекции мы обсудим один из самых интересных и мощных методов в геометрической оптике . Как мы обсуждали в лекции III, геометрическая оптика — это тот сегмент оптики, в котором мы ограничены ситуацией, когда длина волны света пренебрежимо мала , например, незначительна по сравнению с размером объектов, с которыми взаимодействует световая волна. .
Мы узнаем много деталей о том, что такое световая волна, в будущих лекциях этой серии. Многие из них уже доступны на этом веб-сайте, например см. вторую ссылку ниже.
(лекция — III) Подробнее о «геометрической оптике»
(Волны) Прочтите о свете как о волне
Как следствие, свет (волны) можно рассматривать как луча, или геометрические прямые линии, а нюансы света как колебания волн можно отложить до счастливого часа.
Трассировка лучей
В пределах геометрической оптики любая общая оптическая система может быть связана с лучом, который можно проследить с помощью двух основных типов пересечения луча: смещения и преломления . Таким образом, закон преломления является центральным инструментом для трассировки лучей . Луч можно описать в оптической системе с помощью его координат . Скоро мы определим координаты лучей.
Наша цель — найти матрицу, которая управляет перемещением луча от одной координаты к другой координате, когда луч перемещается от одной геометрической точки к другой.Это позволит нам изучать как простые, так и гораздо более сложные системы наиболее эффективным и действенным способом, как мы увидим.
Давайте обсудим основные матрицы, доступные для трассировки лучей, когда луч перемещается от одной координаты к другой в следующих двух случаях.
- I. Матрица перевода Матрица перевода
- актуальна, когда свет распространяется по прямой линии в однородной среде
- II. Матрица преломления Матрица преломления
- относится к преломлению, возникающему на границе раздела двух разных сред
Таким образом, в общем, пересечения луча по сети могут составлять любое количество из перемещений, и любое количество из рефракций, .Отражение будет просто двумя переводами, а общее преломление может быть истолковано как из преломления, так и из перевода, как мы увидим.
Таким образом, наиболее обобщенная оптическая система может иметь количество трансляций и количество рефракционных матриц , так сказать, в их соответствующих порядках. Итоговая или результирующая матрица будет называться системной матрицей .
I. Матрица перевода
Давайте рассмотрим луч, который пересекает оптическую среду по прямой линии под любым углом.Это называется перемещением , поскольку единственное изменение, которому подвергается луч, — это перенос или прямолинейное смещение координат. Излишне говорить, что это заставляет нас понять, что луч ограничен одной однородной средой .
Формулировка матрицы в геометрической оптике : Перевод относится к трассировке лучей в единой однородной среде. Координаты луча преобразуются из одной точки (например, P) в другую точку (например, M или Q) посредством матричной формулировки оптической системы. Фотография предоставлена : mdashf.orgОбратите внимание, что на приведенной выше диаграмме мы показали две разные линзы, матрица трансляции поможет нам только до точки Q. Нам потребуется дальнейшая формулировка (матрица преломления), чтобы увидеть, что происходит. происходить внутри одной или нескольких линз или любого другого оптического носителя.
Луч был бы полностью охарактеризован, если бы мы могли указать необходимое количество координат луча, каким бы сложным он ни был. В нашем случае это просто, прямолинейное.Поэтому нам нужно указать координаты любых двух точек, чтобы полностью указать наш луч.
В любой геометрической точке луча ее координата задается двумя переменными; высота от оси (показана на рисунке PP ’для и MM’ для) и угол от оси посредством или (например, или).
Мы определили наш луч в двух точках — следовательно, определили его полностью, указав две координаты (высота и угол — координаты луча ) — в двух разных геометрических точках (P и M — геометрические точки луча ). ): i.е. координатами (луча) в геометрической точке P и координатами (луча) в геометрической точке M.
Мы определяем еще одну удобную переменную, косинус оптического направления ; это шаг ближе к определению оптических путей. Косинус оптического направления значительно упрощает жизнь, когда мы имеем дело с оптическими ситуациями. Если вам интересно узнать, как определяется оптический путь, перейдите по ссылке.
(Как определяется оптический путь?) Нажмите, чтобы узнать больше об оптическом пути
Показатель преломления пригодится, даже если нам нравится простота этой конкретной проблемы однородной среды.Эта новая переменная (косинус оптического направления) имеет вид.
На нашем рисунке, показанном выше, луч движется по прямой линии в однородной среде. Отсюда . Также . Если мы примем параксиальную область, это будет означать:. Это еще больше изменило бы уравнения, которые у нас только что были:. Также имеем от этого: и.
(Что такое параксиальная область?) Щелкните, чтобы увидеть, что означает параксиальная область
Опять же, поскольку наша среда однородна. Поскольку мы движемся по прямой, имеем: и.
Выражения в можно записать в терминах матриц:.
Таким образом, луч в координате переходит в координату, и это движение представлено матрицей, известной как матрица перевода, где,.
Фактическое расстояние, пройденное лучом в однородной среде, приблизительно равно, и это основано на нашем параксиальном предположении . Мы тоже это видим.
II. Матрица преломления
Мы определили форму матрицы, которая будет отвечать за перенос луча от его начальной координаты к его конечной координате, если пересечение рассматриваемого луча происходит в единой однородной среде и следует по прямой.
Более сложный процесс — это процесс, в котором луч преломляется при встрече с поверхностью раздела двух сред с разными показателями преломления. Анализируя прохождение луча, мы можем определить матрицу, которая управляет прохождением луча для преломления. Соответственно, мы называем ее рефракционной матрицей .
Нарисуем подходящую диаграмму для этой ситуации. Мы рассмотрим одну преломляющую поверхность и оставим без внимания любую дальнейшую конфигурацию поверхности. Таким образом, мы можем позже перейти к конфигурациям, которые могут иметь разную толщину и разные вторичные поверхности, после единственной поверхности слева, которая является сферической с кривизной радиуса.
Формулировка матрицы в геометрической оптике : Матрица преломления; Матрица преломления относится к трассировке лучей в неоднородных средах. Координаты лучей преобразуются из одной точки в другую в неоднородных средах с помощью мощной матричной формулировки оптических систем. Фотография предоставлена : mdashf.orgПоскольку луч теперь проходит через две среды, преломляясь на стыках этих сред, мы должны задействовать закон Снеллиуса , чтобы ограничить путь луча.
Кроме того, мы непреклонны в отношении параксиального пересечения луча, то есть луч держится как можно ближе к оптической оси, как по высоте, так и по углу, поэтому величина углов и т. Д. Будет приближена к величине самих углов. , учитывая, что углы уже последовательно указаны в радианах.
а. закон Снеллиуса приводится в и b. параксиальное допущение дается формулой.
Также мы записываем отношения между углами, как показано на диаграмме выше, чтобы мы могли выразить все в терминах наших ранее определенных координат луча, в терминах.
Итак, у нас есть где — углы, образованные падающим лучом и преломленным лучом с осью z, то есть оптической осью. Также — это угол, образованный нормалью (обозначенной как N) к преломляющей сферической поверхности с осью z.
— это показатели преломления среды до преломляющей поверхности и среды после преломляющей поверхности соответственно.
Значит наше параксиальное допущение. Таким образом, у нас есть from, и мы имеем:.
Если бы мы определяли, у нас было бы. называется силой преломляющей поверхности.
Теперь отметим, что высота луча в точке-P до и после преломления одинакова, поэтому:. вместе можно записать в виде матричного уравнения:. называется матрицей преломления, так что.
III. Системная матрица
В общем, любая оптическая система состоит из серии преломляющих и поступательных движений луча. Таким образом, мы можем написать общую матрицу, которая преобразует координаты из одной точки конфигурации в другую при нашем параксиальном предположении.
, где называется системной матрицей . Соответственно, матрица системы является произведением любого количества возможных матриц преломления и трансляции . Это легко увидеть, так как, и.
Это означает, что элементы матрицы системы в целом удовлетворяют условию. безразмерны, имеют размерность обратной длины и размерность длины.
Матрица в этой форме также называется матрицей ABCD из-за символов элементов,.
20,639775 85,5
Mahisapat, Dhenkanal, Odisha 759001, India
Нравится:
Нравится Загрузка …
СвязанныеМатричная оптика Фурье позволяет создать компактную камеру с полной стоксовой поляризацией.
Метаповерхностная поляризационная камера.
Отображение поляризации света, рассеянного от объекта, обеспечивает дополнительную степень свободы для получения информации из сцены. Обычные поляриметры могут быть громоздкими и обычно состоят из механически движущихся частей (с вращением поляризатора и анализатора для определения степени поляризации).Рубин и др. Компания разработала полностью стоксову компактную поляризационную камеру на основе метаповерхностей без традиционной поляризационной оптики и движущихся частей. Результаты обеспечивают упрощенный путь для поляризационного изображения.
Наука , этот выпуск стр. eaax1839
Структурированный реферат
ВВЕДЕНИЕ
Поляризация описывает путь, по которому колеблется вектор электрического поля света. Важное качество электромагнитного излучения, поляризация, часто не учитывается при его математической обработке.Тем не менее поляризация и ее измерение представляют интерес практически во всех областях науки, а также в технологиях получения изображений. Традиционные камеры чувствительны только к интенсивности, но в различных контекстах знание поляризации может выявить особенности, которые в противном случае невидимы. Для определения полного вектора Стокса — наиболее полного описания поляризации света — требуется как минимум четыре отдельных измерения. В результате оптические системы часто бывают громоздкими, зависят от движущихся частей и имеют ограниченное временное разрешение.
ОБОСНОВАНИЕ
Мы вводим формализм — матричную оптику Фурье — для рассмотрения поляризации в параксиальной дифракционной оптике. Этот формализм является мощным обобщением большого объема прошлых работ по оптическим элементам, поляризация которых может изменяться в пространстве. Более того, он предлагает путь к параллельной реализации множества поляризационных устройств с использованием одного оптического элемента. Затем мы можем спроектировать дифракционные решетки, порядки которых действуют как поляризаторы для произвольно выбранного набора состояний поляризации, нового класса оптических элементов.Затем интенсивность света в наборе порядков дифракции определяется поляризацией освещающего света, что делает эти решетки незамедлительно применимыми для получения изображений с полной стоксовой поляризацией.
РЕЗУЛЬТАТЫ
Мы теоретически исследуем эти решетки и разработаем схему оптимизации их конструкции. Наши дифракционные решетки были выполнены с диэлектрическими метаповерхностями, в которых субволновые анизотропные структуры обеспечивают настраиваемое управление поляризацией на видимых частотах.Характеристики изготовленных решеток показывают, что они работают так, как задумано. Примечательно, что произвольный набор поляризаций может быть проанализирован с помощью одной элементарной ячейки, в отличие от прошлых подходов, которые основывались на чередовании нескольких индивидуально разработанных дифракционных решеток, увеличивая гибкость этих устройств.
Эти решетки позволяют делать снимки, камеру с полной стоксовой поляризацией — камеру, получающую изображения, в которых полное состояние поляризации известно в каждом пикселе, без традиционной поляризационной оптики и движущихся частей (см. Панель A на рисунке).Поляризованный свет от фотографической сцены падает на решетку внутри камеры. Поляризация «сортируется» с помощью специально разработанной субволновой метаповерхностной решетки. В сочетании с оптикой формирования изображения (линзой) и датчиком на датчике формирования изображения формируются четыре копии изображения, соответствующие четырем порядкам дифракции. Каждая из этих копий фактически проходит через другой поляризатор, функции которого встроены в метаповерхность. Четыре изображения могут быть проанализированы по пикселям, чтобы восстановить четырехэлементный вектор Стокса по всей сцене.Несколько примеров показаны на длине волны 532 нм как в помещении, так и на открытом воздухе. На рисунке показан пример фотографии двух пластиковых деталей, изготовленных литьем под давлением, линейки и ложки (освещенных линейно поляризованной подсветкой), на которых видны внутренние напряжения (см. Панели C — E рисунка), которые не проявляются в традиционная фотография (панель B). Камера компактна, требует только решетки (которая является плоской и монолитно интегрированной, выполняющей весь анализ поляризации в системе), линзы и обычного датчика CMOS (дополнительный металл – оксид – полупроводник).
ЗАКЛЮЧЕНИЕ
Таким образом, метаповерхности могут упростить и уменьшить площадь основания оптических систем, основанных на поляризационной оптике. Наш проектный формализм предлагает направления будущих исследований в поляризационной оптике. Более того, он позволяет создавать моментальные снимки с системой формирования изображений с полной стоксовой поляризацией без движущихся частей, без оптики с объемной поляризацией и без специально структурированных пикселей камеры, что в целом не является более сложным, чем обычная система формирования изображений. Наше оборудование может позволить использовать поляризационные изображения в приложениях (дистанционное зондирование, атмосферная наука, машинное зрение и даже бортовые автономные транспортные средства), где в противном случае их сложность могла бы оказаться непомерно высокой.
Поляризационная камера на основе метаповерхности.( A ) Фотографические сцены содержат поляризованный свет, который невидим для традиционных изображений, основанных на интенсивности, которые могут выявить скрытые особенности. В нашей камере используется метаповерхность (вставка), которая направляет падающий свет в зависимости от его поляризации, формируя четыре копии изображения, которые позволяют реконструировать поляризацию. (От B до E ) Пластиковая линейка и ложка фотографируются камерой.(B) Монохромное изображение интенсивности (заданное компонентом S 0 вектора Стокса) не раскрывает богатую поляризационную информацию, проистекающую из двойного лучепреломления под напряжением, которая легко проявляется в (C) — (E), которые показывают необработанные экспозиция, азимут эллипса поляризации и компонент S 3 вектора Стокса, который описывает содержание круговой поляризации, соответственно.
Abstract
Последние разработки позволили на практике реализовать оптические элементы, в которых поляризация света может изменяться в пространстве.Мы представляем расширение Фурье-оптики — матричную Фурье-оптику — для понимания этих устройств и применения его для проектирования и реализации метаповерхностных решеток, реализующих произвольный параллельный поляризационный анализ. Мы покажем, как эти решетки позволяют создать компактную полностоксову поляризационную камеру без стандартной поляризационной оптики. Наша поляризационная камера с однократным снимком не требует движущихся частей, пикселей с особым рисунком или обычной поляризационной оптики и может обеспечить широкое применение поляризационной визуализации в машинном зрении, дистанционном зондировании и других областях.
Поляризация относится к пути, который проходит вектор электрического поля света. Как фундаментальная характеристика света, поляризация и ее измерение представляют большой интерес почти во всех областях науки, а также в технологии получения изображений. Традиционно поляризация рассматривается как свойство луча света. Однако достижения последних нескольких десятилетий в голографических средах, микро- и нанофабрикации и других областях позволили на практике реализовать оптические элементы с заданными пространственно изменяющимися поляризационными свойствами, даже в субволновом масштабе, на оптических частотах.В этих устройствах состояние поляризации света может контролироваться от точки к точке через оптический элемент.
Работы такого рода теперь имеют обширную литературу по нескольким дисциплинам оптики под разными названиями, включая дифракционную оптику ( 1 , 2 ), поляризационную голографию ( 3 — 6 ) и нанофотонику (метаповерхности). ( 7 , 8 ), в дополнение к заметному вниманию со стороны сообщества жидких кристаллов ( 9 , 10 ).Эти устройства демонстрируют различное поведение в зависимости от поляризации освещающего света, поэтому возникает естественный вопрос, как они могут быть разработаны для параллельной реализации многих зависимых от поляризации функций.
Мы рассматриваем обобщение работы в этой области, которую мы называем матричной оптикой Фурье, которая предлагает новые стратегии проектирования для создания поляризационной оптики, ранее недостижимые в одном элементе. В частности, мы применяем его для создания дифракционных решеток на метаповерхностях, которые могут параллельно анализировать несколько произвольно заданных состояний поляризации.
Матричная оптика Фурье
Мы представляем общий способ наблюдения дифракции от поляризационно-зависимого препятствия. В картине расширения плоских волн (или углового спектра) оптики электромагнитное возмущение U (x, y) в плоскости можно рассматривать как образованное интерференцией множества плоских волн, падающих под разными углами. Отдельная плоская волна в этом наборе характеризуется своим волновым вектором в плоскости (kx, ky) и весом, задаваемым преобразованием Фурье оптического поля как
A (kx, ky) = ∬ − ∞ + ∞U ( x, y) ei (kxx + kyy) dx dy (1)Каждая плоская волна со своим весом A (kx, ky) может индивидуально распространяться вперед в пространстве, чтобы сформировать поле в другом месте (рис.1А). Этот формализм позволяет рассматривать взаимодействие света с простыми препятствиями. Если плоское препятствие, имеющее функцию пропускания t (x, y) (например, двойная щель Юнга или дифракционная решетка), освещается падающим полем с величиной E0 (которое также может изменяться в пространстве), поле сразу после препятствие, t (x, y) E0, можно преодолеть таким образом.
Рис. 1 Матричная фурье-оптика.( A ) Скалярное оптическое поле U (x, y) имеет разложение A (kx, ky) плоской волны, полученное преобразованием Фурье (F), которое позволяет ему распространяться вперед в пространстве.( B ) Препятствие, реализующее матрицу Джонса J˜ (x, y) 2 × 2, которая изменяется в зависимости от пространства (и, таким образом, содержит четыре скалярные функции, которые здесь схематично представлены в виде различных плоскостей), имеет представление A˜ в области Фурье. (kx, ky), которая также является матрицей Джонса. A˜ (kx, ky) кодирует поведение направления (kx, ky) как функцию падающей поляризации. ( C ) Если J˜ (x, y) представляет собой периодическую решетку, ее порядки описываются коэффициентами матрицы Джонса J˜ (kx, ky), каждый из которых описывает независимое поляризационное устройство, например, конфигурацию двулучепреломляющих пластин.Решетка реализует множество таких устройств параллельно.
Это интуитивное понимание распространения оптических волн является основой области, широко известной как оптика Фурье ( 11 ), и лежит в основе большей части современной оптической физики, включая визуализацию и голографию. Примечательно, однако, что эта картина является скалярной и не включает поляризацию света. Тем не менее, можно представить себе оптические элементы, в которых свойства, зависящие от поляризации, изменяются в зависимости от пространства.Тогда вместо скалярной функции передачи t (x, y) мы можем считать, что оптический элемент связан с матричнозначной функцией J˜ (x, y). Здесь J˜ (x, y) обозначает локальную матрицу Джонса ( 12 ), способ модификации вектора поляризации Джонса в каждой точке. (В данной работе матричные величины обозначены тильдой.)
Считаем, что такой оптический элемент с матричным профилем Джонса J˜ (x, y) освещается полем, описываемым вектором Джонса ket | E0〉 ( в знак признания его поляризованного характера).Поле сразу после препятствия тогда задается формулой J˜ (x, y) | E0〉. Это поле также может распространяться за счет расширения плоских волн, как задается преобразованием Фурье | A (kx, ky)〉 = ∬ − ∞ + ∞J˜ (x, y) | E0〉 ei (kxx + kyy) dx dy (2), который теперь векторнозначен. Если падающая волна является нормально падающей однородной плоской волной, она не будет иметь пространственной зависимости и может быть исключена из интеграла. Таким образом, единственный интеграл, который необходимо вычислить, равен A˜ (kx, ky) = ∬ − ∞ + ∞J˜ (x, y) ei (kxx + kyy) dx dy (3), который является интегралом Фурье, распределенным по каждому четырех элементов матрицы Джонса 2 × 2, что дает коэффициент Фурье A˜ (kx, ky), который сам является матрицей Джонса (рис.1Б).
Это матричное преобразование Фурье имеет физическое значение. Вместо амплитуды и фазы, как в традиционной оптике Фурье, данное направление (kx, ky) связано с поляризационно-зависимым поведением, задаваемым матричным оператором Джонса A˜ (kx, ky). В некотором смысле это описание отделяет оптический элемент, описываемый J˜ (x, y), от поляризации освещающего света: взаимодействие всех возможных падающих поляризаций с J˜ (x, y) сразу обрабатывается матрицей Фурье преобразовать A˜ (kx, ky).
В этой работе мы специализируемся на поляризационно-зависимых дифракционных решетках, то есть элементах, в которых J˜ (x, y) является периодической функцией, а угловой спектр A˜ (kx, ky) дискретен, что дает дифракционные порядки. Дифракционные решетки просто показывают последствия этой матричной фурье-оптики, в частности то, что ее можно инвертировать и использовать в качестве стратегии проектирования многофункциональной поляризационной оптики. Предположим, что существует набор желаемых поляризационных устройств, которые необходимо реализовать (например, поляризаторы, волновые пластины, оптически активные элементы или любое поведение, которое может быть описано матрицей Джонса), имеющее матрицы Джонса {J˜k} и набор порядков дифракции {ℓ}.Разложение в ряд Фурье J˜ (x, y) = ∑k → ∈ {ℓ} J˜kei (kxx + kyy) (4) представляет собой единственный оптический элемент, реализующий все эти (потенциально сложные) поляризационно-зависимые функции параллельно каждому порядок реализации собственного поляризационного устройства (рис. 1в). В случае решетки преобразование Фурье Ур. 3 становится рядом Фурье в уравнении. 4 с оптическими элементами {J˜k} в качестве коэффициентов. Мы называем такую дифракционную решетку матричной решеткой.
Этот способ просмотра поляризационно-зависимой дифракции не получил широкого признания или использования в литературе по поляризации [с некоторыми ограниченными исключениями в дифракционной оптике ( 13 , 14 ) и трассировке поляризационных лучей ( 15 , 16 )].В общей стратегии оптические элементы — особенно в области метаповерхностей — часто проектируются таким образом, что при падении заданной поляризации состояние выходной поляризации является однородным по всему элементу и передается скалярный фазовый профиль. Когда падает ортогональная поляризация, состояние выходной поляризации снова становится однородным, и наблюдается второй профиль фазы. Таким образом, могут быть реализованы оптические элементы с различными функциями для выбранных базисов линейной, круговой и произвольной эллиптической поляризации ( 7 , 8 , 17 ).Примечательно, что то, что широко называют «геометрической» фазой или фазой «Панчаратнам-Берри», по крайней мере в том, что касается этой проблемы, является частичным случаем этого подхода, используемого для создания скалярных фазовых профилей для циркулярно поляризованного света ( 2 , 9 , 18 — 21 ). В других прошлых работах подразумевается, что поляризация изменяется в зависимости от пространства, но предполагается конкретное падающее состояние поляризации ( 22 , 23 ). Эти прошлые стратегии проектирования являются частями представленного здесь матричного подхода.
Анализ параллельной поляризации с помощью унитарных поляризационных решеток
Формализм, представленный в последнем разделе, является общим. Уравнение 4 дает рецепт реализации дифракционного элемента, реализующего произвольное поведение поляризации, но не определяет природу желаемых оптических функций (содержащихся в {J˜k}) или то, как должен быть получен результирующий J˜ (x, y) практически реализовано.
Мы сосредотачиваемся на случаях, когда {J˜k}, поведения, реализуемые порядками решетки, являются анализаторами поляризации.Этот выбор не является принципиальным, но он очень актуален для практических приложений: анализаторы, возможно, являются наиболее фундаментальным поляризационным элементом, и, более того, устройства, которые проецируют свет на различные состояния поляризации, имеют практическое применение в поляриметрии, измерении поляризации света. состояние ( 24 ). Порядок дифракции k , ведущий себя как поляризатор, может быть описан матрицей Джонса, которая является диадическим (внешним произведением), выраженным как
J˜k = ak | pk〉 〈qk | (5)Уравнение 5 описывает матрицу Джонса, анализирующую для выбранного вектора Джонса | qk〉 в соответствии с законом Малуса: когда падает | qk〉, передача интенсивности максимальна.Если вместо этого приходит ортогональная поляризация | qk⊥〉 с 〈qk⊥ | qk〉 = 0, выходной свет гасится. Свет, выходящий из J˜k, будет нести состояние поляризации | pk〉. (Традиционный поляризатор, знакомый по лабораторному опыту, имеет | pk〉 = | qk〉. Наконец, ak — комплексный (скалярный) вес.
После того, как требуемые анализаторы {J˜k} определены (уравнение 5), решетка J˜ (x, y) может быть получена с помощью уравнения. 4. Какой физический оптический элемент должен реализовывать результирующее J˜ (x, y)? Очень удобная среда реализации представляет собой метаповерхности ( 25 , 26 ) — субволновые массивы нанофотонных фазовращателей, состоящих из диэлектрических столбов, обладающих двойным лучепреломлением ( 7 , 8 ).Локально матрица Джонса этих метаповерхностей может быть хорошо аппроксимирована линейно двулучепреломляющей волновой пластиной ( 8 ), задаваемой формулой
J˜ (x, y) = R (θ (x, y)) (eiϕx (x, y) 00eiϕy (x, y)) R (−θ (x, y)) (6)Другими словами, такая метаповерхность может реализовывать дискретизированную матричную решетку, где J˜ (x, y) локально имеет форму Ур. 6. Использование диэлектрических метаповерхностей, подчиняющихся уравнению. 6, опять же, не принципиальный выбор, но особенно удобный: все ϕx, ϕy и θ легко и непрерывно регулируются путем изменения размеров и угловой ориентации простого диэлектрического столба, легко изготовленного литографически (R — это 2 × 2 матрица вращения).Мы называем мета-диаграммы, построенные из этих элементов, просто «решетками», но в отличие от более общих дифракционных решеток, следует понимать, что решетки здесь обладают особыми поляризационными свойствами из-за их субволновых характеристик.
При осмотре уравнение. 6 описывает матрицу Джонса, которая (i) унитарна всюду, то есть J˜ † J˜ = 1 для всех (x, y), с 1 единичной матрицей 2 × 2, и, более конкретно, (ii) линейно двулучепреломляющая, имеющий линейные поляризации в качестве собственных векторов для всех (x, y).
Из представленной полностью общей матричной картины мы сделали два конкретных выбора, согласно которым дифракционные порядки решетки должны вести себя как анализаторы, и что решетка должна локально напоминать уравнение. 6, что подразумевает два вышеуказанных ограничения. Но согласуются ли эти варианты друг с другом математически? То есть для общего набора порядков дифракции {ℓ}, реализующего анализаторы поляризации J˜k = ak | pk〉 〈qk | для k∈ {ℓ} будет J˜ (x, y), предписанное уравнением. 4 подчиняются форме уравнения. 6 для всех (x, y)?
Этот вопрос является матричным аналогом обширной работы, проведенной на фазовых решетках ( 27 , 28 ).Мы показываем в дополнительном тексте (раздел S1), что линейное двойное лучепреломление, требуемое уравнением. 6 следует, что J˜k должен быть симметричным, что означает, что каждый из них имеет вид J˜k = ak | qk *〉 〈qk |. То есть выходная поляризация каждого анализатора должна быть комплексным сопряжением анализируемого вектора Джонса; это эквивалентно зеркальному отражению относительно экваториальной плоскости сферы Пуанкаре, изменению знака третьей (киральной) компоненты Стокса. Физически это означает, что анализатор оставляет форму эллипса поляризации неизменной, меняя направление вращения на противоположное, что является обобщением ключевого вывода ( 7 ) и ( 8 ).
Принятие этого ограничения гарантирует линейное двойное лучепреломление (то есть матричную симметрию) для всех (x, y), но не обязательно везде унитарность. Это ограничение унитарности, в частности, означает, что, если мы настаиваем на матричной решетке с точно n порядками, которые являются анализаторами состояния поляризации, форма уравнения 6 может быть сопоставлен везде, только если n = 2 и поляризации, анализируемые для, строго ортогональны (как доказано в дополнительном текстовом разделе S1) ( 17 ).
Стратегия проектирования и оптимизация
Если мы настаиваем на использовании однослойной метаповерхности, подчиняющейся уравнению. 6, то мы не можем ограничить весь свет произвольным набором порядков дифракции, действующим как анализаторы состояния поляризации. Но что, если некоторый свет может проникнуть в другие порядки дифракции? Тогда J˜k одних порядков могли бы вести себя как анализаторы для произвольных состояний поляризации с ограниченным количеством утечек в другие порядки дифракции (реализуя свои собственные J˜k), так что вся решетка, сформированная в уравнении.4 по-прежнему унитарен везде. Другими словами, решетка может функционировать как связанная система, в которой соседние порядки дифракции компенсируют желаемое поведение, зависящее от поляризации, на нескольких избранных таким образом, чтобы сохранить общую унитарность для всех (x, y).
Здесь мы стремимся создать решетку J˜ (x, y), которая локально подчиняется уравнению. 6 с набором порядков дифракции {ℓ}, каждый из которых имеет J˜k, которые являются анализаторами для произвольно заданного набора состояний поляризации {| qk〉}, как определено в уравнении. 5 с как можно меньшим количеством света, проникающего в дифракционные порядки за пределами {ℓ}.Это вопрос оптимизации. Определим величины Iqk = 〈qk | J˜k † J˜k | qk〉, степень дифракции k при падающей преимущественной поляризации | qk〉 и Iq⊥k = 〈qk⊥ | J˜k † J ˜k | qk⊥〉, мощность дифракционного порядка k , когда падает ортогональная поляризация | qk⊥〉 с 〈qk⊥ | qk〉 = 0. Сумма ∑k∈ {ℓ} Iqk должна быть максимальной, чтобы сохранить как можно больше света в интересующих нас порядках. Одновременно контраст каждого порядка, задаваемый формулой η = (Iqk − Iq⊥k) / (Iqk + Iq⊥k) — поляризационная чувствительность порядка к желаемой поляризации | qk〉, — должен быть как можно ближе к единице, чтобы заставляют J˜k действовать как желаемые анализаторы (в смысле Ур.5). Эту проблему можно решить с помощью градиентного спуска. Мы оставляем подробное обсуждение этой оптимизации в дополнительном тексте [разделы S1 и S2, где мы также описываем путь к аналитической форме решения с использованием вариационных методов ( 17 , 27 , 28 )].
Во многих предыдущих работах рассматривались дифракционные решетки, способные расщеплять и, таким образом, анализировать свет на основе его состояния поляризации. Однако в этих работах обычно использовался скалярный подход, стремясь придать фазовые профили решетки противоположного свечения на состояниях ортогональной поляризации.Следовательно, несколько индивидуально разработанных решеток должны быть чередованы (часто называемые «пространственным мультиплексированием» или «общей апертурой») ( 29 — 32 ) или, что эквивалентно, последовательно соединены каскадом ( 1 , 33 ) для создания решетка, порядки которой анализируются для любых более чем двух состояний поляризации. Это по своей сути проблематично: в этих конфигурациях невозможно реализовать поляриметрию с использованием менее шести измерений (в то время как четыре — это минимум), что ставит под угрозу пространство сенсора.Более того, состояния поляризации анализаторов не могут быть заданы произвольно. Чередование различных решеток также вносит нежелательную периодичность, вызывая потерю света из-за дифракции вне плоскости. Матричный подход в этой работе показывает, что чересстрочная развертка не является необходимой — все функции могут быть объединены в одну решетку — и, более того, предоставляет возможности, недостижимые с помощью чересстрочной развертки. Тетраэдрическая решетка, которую мы представим в качестве простого примера, невозможна простым чередованием, поскольку ни одно из четырех ее состояний анализатора не ортогонально какому-либо из других.
Эксперимент
Конструкция решетки тетраэдра
Решетки, реализующие анализ параллельной поляризации, представляют практический интерес для поляриметрии Стокса ( 24 , 34 ), которая требует минимум четырех измерений состояния проективной поляризации. Для максимальной точности восстановления вектора Стокса эти четыре состояния должны быть настолько отличными друг от друга, насколько это возможно, что достигается путем выбора состояний анализатора, соответствующих тетраэдру, вписанному в сферу Пуанкаре (пространство состояний поляризации) ( 35 — 37 ).Мы используем матричный формализм и схему оптимизации, описанные выше, для создания двумерной дифракционной решетки, анализирующей эти четыре состояния поляризации на ее внутренних четырех порядках. На крайней левой панели рис. 2A представлена карта этих порядков и эллипсов поляризации ({| qk〉}), которые они предназначены для анализа в пространстве k . Эти порядки дифракции и желаемые состояния поляризации могут быть введены в вышеупомянутую оптимизацию, давая числовое значение J˜ (x, y), которое локально имеет форму Ур.6 (унитарное и линейное двулучепреломляющее). Затем легко отобразить локально требуемую матрицу Джонса (ϕx, ϕy, θ) на геометрию реальных структур, обратившись к библиотеке таких структур в интересующем режиме платформы материала / длины волны ( 8 ).
Рис. 2 Матричные решетки для анализа произвольной параллельной поляризации.( A ) Элементарная ячейка с двумерной решеткой предназначена для анализа четырех состояний поляризации, соответствующих тетраэдру, вписанному в сферу Пуанкаре.Слева представлена карта порядков дифракции и эллипсов поляризации, которые они анализируют в k-пространстве. Спроектированная элементарная решетчатая ячейка с 11 × 11 элементами, содержащая TiO 2 прямоугольных столбов, реализующая это на λ = 532 нм, показана в дизайне (в центре) и в заводском исполнении [сканирующая электронная микрофотография (SEM), справа]. Масштабная линейка, 1 мкм. ( B ) Решетка освещается светом, поляризация которого изменяется при регистрации выходной поляризации в одном порядке дифракции с помощью полностоксова поляриметра, позволяющего реконструировать экспериментальную матрицу Мюллера M˜ (m, n) порядка 4 × 4.( C ) Показан поляризационный контраст каждого порядка. Каждый порядок помечен эллипсом поляризации, который он анализирует, и приведены результаты аналитической конструкции решетки (оптимизированная, красный), двухполупериодного моделирования решетки (синий) и эксперимента (зеленый). ( D ) Поляризации, проанализированные по каждому порядку [для которого они имеют контрасты, указанные в (C)] решетки тетраэдра, показаны на сфере Пуанкаре рядом с тетраэдром, указывающим желаемую поляризацию анализатора, как предсказано оптимизацией, полный -волновое моделирование и измерение.( E ) Набор из 1024 однородно дискретизированных состояний входной поляризации на сфере Пуанкаре может использоваться с помощью экспериментально определенной матрицы Мюллера M˜ (m, n) для формирования искаженного набора состояний, изображающих выходную поляризацию как функцию входной . Каждая сфера справа представляет поведение одного из четырех спроектированных порядков решетки, для которых показаны расчетные поляризации анализатора. На каждом из них синяя стрелка обозначает измеренную поляризацию анализатора | q (m, n)〉 из (C), красная стрелка — зеркально отраженная на экваторе поляризация | q (m, n) *〉, а зеленая стрелка — среднюю выходную поляризацию. по всем точкам, которые согласно формализму здесь должны перекрываться с красной точкой.(В некоторых случаях перекрытие красных и зеленых стрелок слишком близко, чтобы обеспечить визуальное различение.)
В этой работе эта материальная платформа представляет собой колонны из TiO 2 , изготовленные с помощью литографии с электронным пучком и техникой осаждения атомного слоя, подробно документированной в другом месте ( 38 ). Это позволяет работать в технологически важных видимых длинах волн, помогая описанному ниже приложению камеры. Однако мы подчеркиваем, что ни TiO 2 , ни видимые длины волн не являются центральными для этой работы.Представленные здесь элементарные ячейки решетки имеют 11 таких элементов на стороне с межэлементным расстоянием 420 нм, так что угол дифракции на λ = 532 нм составляет θD∼6.6 ° (параксиальный). Субволновое расстояние между опорными элементами гарантирует, что радиационные порядки могут происходить только из коллективной элементарной ячейки 11 × 11 элементов. Решетчатая элементарная ячейка, разработанная путем оптимизации для случая тетраэдра, показана на рис. 2А (вверху и внизу соответственно) как в конструкции, так и в заводском исполнении (электронная микрофотография, справа).Эта элементарная ячейка сотнями раз мозаична, чтобы создать решетку.
Поляриметрия матрицы Мюллера и результаты
В поляризационной оптике матрицы Джонса и Мюллера описывают поляризационно-зависимое поведение. Из этих двух только матрица Мюллера является непосредственно наблюдаемой, поскольку она описывает оптические интенсивности, а не электрические поля. С этой целью мы выполняем поляриметрию матрицы Мюллера, то есть экспериментальное определение матрицы Мюллера 4 × 4 M˜ (m, n) каждого из четырех порядков решетки (m, n), представляющих интерес (как двумерная решетка, заказы помечены двумя целыми индексами).Решетка освещается лазерным светом с λ = 532 нм в нескольких (не менее четырех) различных состояниях входной поляризации с известными векторами Стокса {S → in}. Поскольку поляризация переключается между различными известными входами, можно установить поляриметр полного Стокса в интересующем порядке для записи соответствующих выходных векторов Стокса, {S → out}. Матрица M˜ (m, n), связывающая {S → in} с {S → out}, затем может быть численно определена из данных в смысле наименьших квадратов. Это схематично показано на фиг. 2B и более подробно обсуждается в дополнительном текстовом разделе S3 ( 17 ).
При анализе результатов трудно провести прямое сравнение матричных величин. Вместо этого, поскольку каждый интересующий порядок предназначен для работы в качестве анализатора поляризации, имеет смысл задать следующие вопросы: действуют ли заказы как анализаторы? Для каких поляризаций? И с какой эффективностью?
Первый вопрос отвечает на рис. 2C, на котором изображен поляризационный контраст каждого порядка дифракции. Каждая группа полос на фиг. 2C соответствует порядку дифракции, предназначенному для анализа эллипса поляризации, показанного под ним.Каждая группа содержит три столбца с цветовой кодировкой: один для численно оптимизированного J˜ (x, y), один для полноволнового моделирования и один для измерения. Слева на рис. 2D показан контраст (нормализованная разница между интенсивностью в том порядке, когда его предпочтительная поляризация падает, по сравнению с ортогональной). Идеальный поляризатор имел бы 100% контраст. Численно оптимизированный результат показывает, что результат близок к совершенству (100%). При моделировании конструкции решетки контраст несколько уменьшается, а затем снова, как было измерено в действительности.Однако все четыре порядка измеренной решетки показывают поляризационные контрасты, превышающие 90% — разработанные порядки решетки действительно действуют как поляризаторы (анализаторы).
Во-вторых, необходимо проверить, что заказы действуют как анализаторы состояний поляризации, указанных в проекте. На рис. 2D состояния поляризации, для которых каждый порядок решетки имеет максимальную выходную интенсивность (оптимизированная, при моделировании и измеренная), нанесены на сферу Пуанкаре рядом с тетраэдром, представляющим цель конструкции.Можно видеть, что эти поляризации анализатора близки к желаемым (на рис. 2D нет заметных смешений, в результате чего поляризация одного анализатора попадает очень далеко, оказываясь ближе к другой, что ложно преувеличивает соответствие).
На рис. 2, C и D показано, что метаповерхностная решетка реализует четыре произвольно заданных анализатора параллельно без поляризаторов или волновых пластин, что подтверждает обоснованность матричного подхода, лежащего в основе ее конструкции. Мы обращаемся к вопросу эффективности в дополнительном тексте (раздел S3) ( 17 ).Дифракционная эффективность решетки не может быть определена одним числом — она зависит от поляризации. При усреднении по всем возможным входным поляризациям, эффективность с точки зрения мощности, дифрагированной на четыре представляющих интерес порядка, по сравнению с падающей мощностью превышает 50%, что достаточно высоко для практического использования.
Данные, содержащиеся на рис. 2, C и D, получены из первой строки матрицы Мюллера, которая определяет интенсивность S0 выходящего луча. Остальная часть матрицы Мюллера контролирует состояние поляризации выходного луча.Это можно визуализировать, индивидуально оперируя набором входных векторов Стокса, которые единообразно выбирают сферу Пуанкаре (1024 точки) с измеренной матрицей Мюллера M˜ (m, n) каждого порядка, и нанося на график набор векторов Стокса, которые в результате образуют новый, искаженный набор точек. Это показано для каждого из четырех представляющих интерес порядков на рис. 2E на четырех сферах. Если бы каждый из них вел себя как идеальный анализатор (сравните с уравнением 5), все поляризации были бы отображены в единственную точку на искаженной диаграмме в состоянии, соответствующем | pk〉.Решетка не идеальна в экспериментальной реальности, поэтому сферы на рис. 2E содержат точки, распределенные по всей сфере; степень, в которой эти точки сконцентрированы в одном направлении и чрезвычайно редки в других местах, показывает, что каждый порядок дифракции действительно действует как анализатор. Для каждого порядка решетки на рис. 2E синяя стрелка соответствует анализируемой поляризации (скопировано с рис. 2D) (| q (m, n)〉 в обозначениях уравнения 5). Зеленая стрелка показывает поляризацию в порядке решетки, усредненную по набору падающих поляризаций.Наконец, красная стрелка изображает | q (m, n) *〉, который имеет обратную хиральность по отношению к | q (m, n)〉 и, таким образом, отражается относительно экватора сферы. Согласно рисунку, представленному выше, линейное двулучепреломление элементов решетки означает, что выход обязательно должен иметь вид | q (m, n) *〉. Этот аспект теории подтверждается близким перекрытием красных и зеленых стрелок на каждом графике рис. 2E.
В дополнительном тексте результаты приведены для второй решетки, решетки октаэдра, в которой шесть порядков дифракции действуют как анализаторы ( 17 ).
Получение изображений с полной стоксовой поляризацией
Теперь мы применим эти матричные решетки в области, представляющей большой практический интерес. В сочетании с четырьмя детекторами тетраэдрическая решетка, представленная выше, может функционировать как однокомпонентный, компактный и интегрированный полностоксовый поляриметр (датчик для измерения состояния поляризации луча), область, в которой отображаются метаграфикаты ( 29 — 32 ) и комплексные подходы ( 39 , 40 ) в последнее время вызывают значительный интерес ( 34 ).Однако для множества приложений ( 41 — 44 ) поляризационная камера или поляриметр изображения могут оказаться еще более полезными. Поляризационная камера фиксирует вектор Стокса в каждой точке изображения. В случае четырехэлементного вектора Стокса это требует получения четырех независимых изображений по независимым направлениям поляризации, которые могут быть получены последовательно во времени («разделение времени», ограничивающее временное разрешение и часто требующее движущихся частей), путем формирования паттерна. решетку фокальной плоскости с микрополяризаторами («разделение фокальной плоскости», требующее дорогостоящего изготовления, обычно без определения полного вектора Стокса и требующего потери фотонов в поглощающих элементах микрополяризатора) или путем одновременного захвата изображения по четырем тракты, каждый с независимой поляризационной оптикой («разделение амплитуды», существенно увеличивающее объем и сложность системы) ( 41 ).
Подходы на основе решеток не новы для поляриметрии ( 24 , 45 ) (и поляриметрии изображений), особенно в жидкокристаллических ( 46 ) и, в последнее время, в литературе по метаповерхностям ( 29 — 32 ). Однако из-за ограничений предыдущих подходов для выполнения измерений, необходимых для определения полного вектора Стокса, требуется несколько решеток — либо последовательно включенных каскадом, либо расположенных рядом друг с другом.Матричные решетки здесь свободны от этого усложнения, и получение изображений полного Стокса может быть реализовано с помощью одного поляризационного элемента, что открывает широкие возможности для применения в машинном зрении и дистанционном зондировании.
Дизайн системы визуализации
Задача состоит в том, чтобы интегрировать метагрейтинг в систему фотографической визуализации. Тетраэдрическая решетка, описанная выше, выбрана потому, что она обеспечивает определение полного Стокса с помощью всего четырех измерений, что является минимально необходимым. Мы разработали систему формирования изображения, состоящую из этой решетки (реализованной с помощью метаповерхности TiO 2 , как указано выше), за которой следует асферическая линза ( f = 20 мм, выбор которой обсуждается в дополнительном текстовом разделе S4) и стандартной монохромной дополнительной металлической –Оксидно-полупроводниковый (CMOS) датчик изображения.Это изображено на фиг. 3A. Относительно фиг. 2A решетка повернута на 45 °, так что каждый из ее порядков формирует изображение сцены на одном квадранте датчика изображения. Каждый квадрант затем содержит версию фотографии, проанализированную по ее характерной поляризации — эти изображения могут быть получены одновременно, а вектор Стокса S → реконструирован по пикселям (рис. 3B), образуя монохроматическое поляризационное изображение.
Рис. 3 Метаграционная полностоксова поляризационная камера.( A ) Метагрейн матрицы (как на рис. 2) интегрирован с асферической линзой для изображения четырех порядков дифракции на четырех квадрантах датчика изображения CMOS. Показан след луча одного порядка дифракции. Камера предназначена для изображения далеких объектов, поэтому каждый цвет соответствует разным параллельным пучкам лучей, падающим на решетку под разными углами в пределах поля обзора ± 5 °. Не показано: полосовой фильтр 10 нм на длине волны 532 нм и апертура перед решеткой для ограничения поля зрения и предотвращения перекрытия четырех подизображений.( B ) Каждая копия изображения в каждом квадранте анализировалась по разной поляризации. Пиксельные различия в интенсивности можно использовать для синтеза единого поляризационного изображения сцены, в которой полный вектор Стокса известен в каждой точке. ( C ) Более четкий вид луча сбоку на (A). Синий, оранжевый и зеленый соответствуют пучкам лучей, падающим под углом + 5 °, 0 ° и -5 ° соответственно. ( D ) Изображение образца решетки в оптическом микроскопе, равное 1.5 мм в диаметре и показывает зоны Френеля из-за слабого поляризационно-независимого линзирующего эффекта, накладываемого поверх метагрейтинга. На вставке SEM показаны субволновые, двулучепреломляющие столбики TiO 2 , составляющие метаповерхность. ( E ) Система визуализации (A) может быть упакована в практичный портативный прототип с регулируемым фокусом. Основная часть камеры, как показано на (C), имеет длину около 2 см. Прототип здесь больше для удобства оптико-механического монтажа.
Простая трассировка лучей используется для оптимизации всех аспектов системы: разделения решетки и асферы, разделения асферы и датчика изображения и, наконец, периода решетки (и, следовательно, угла дифракции θD). Цель оптимизации состоит в том, чтобы взять параллельные пучки лучей в поле зрения (FOV) ± 5 °, которые, как предполагается, исходят от очень удаленного объекта, и сфокусировать их в пределах квадранта датчика. Азимутально-симметричный, поляризационно-независимый (скалярный) фазовый профиль добавляется поверх матричной решетки во время проектирования и применяется ко всем порядкам дифракции.Это дает слабый эффект линзирования, который помогает при визуализации. Дизайн ориентирован только на один порядок решеток. Тем не менее, остальные три будут отображены в соответствующих квадрантах по умолчанию, потому что система осесимметрична.
Реальный след луча системы формирования изображения показан на рис. 3A с более четким видом сбоку на рис. 3C. Цвета лучей соответствуют параллельным пучкам, падающим под разными углами на решетку матрицы. Оптимизированная решетка имеет N = 10 элементов с шагом 420 нм, что дает θD = 7.3 ° при λ = 532 нм. На рис. 3D показано микроскопическое изображение образца размером 1,5 мм. Образец окружен металлом, чтобы блокировать рассеянный свет, и на нем видны зоны Френеля, возникающие из-за слабого линзирования поверх решетки (периодичность которого слишком мала, чтобы ее можно было увидеть при таком увеличении).
Наконец, вся система может быть упакована в прототип для практического использования в поляризационной фотографии, как показано на рис. 3E, с переменным фокусом. Размер этого прототипа намного больше, чем это необходимо для облегчения оптико-механического монтажа, как показано на рис.3C, функциональная часть системы имеет длину всего ~ 2 см. Апертура перед камерой позволяет управлять полем обзора таким образом, чтобы четыре копии изображения не перекрывались, а полосовой фильтр с длиной волны 10 нм на расстоянии 532 нм за образцом предотвращает влияние дисперсионной природы решетки на формирование изображения. Это важно отметить — если бы в систему формирования изображений был введен широкий диапазон длин волн освещения, решетка эффективно сглаживала бы изображения вместе, а пространственная и спектральная информация размещалась на датчике.Полоса пропускания фильтров на основе красителей, используемых в обычных цветовых датчиках (~ 100 нм для фильтра Байера), слишком велика, чтобы эффективно решать эту проблему. Для получения цветных или гиперспектральных поляризационных изображений может быть использован другой подход, такой как использование настраиваемого фильтра на входе или включение решетки в систему сканирования с нажимной щеткой, в которой единовременно регистрируется только одно пространственное измерение (что является обычным для дистанционное зондирование).
Поляризационное изображение
Затем метаграционная камера может быть использована для практической фотосъемки с полным стоксом.Необработанные данные датчика приблизительно соответствуют фиг. 3B. Чтобы сформировать поляризационное изображение, четыре копии изображения должны быть выровнены (совмещены) друг с другом, образуя вектор I → = [I0 I1 I2 I3] T измеренной интенсивности из четырех квадрантов в каждом пикселе. Если поляризации, проанализированные для каждого порядка дифракции, точно известны (калибровка), вектор Стокса в каждом пикселе может быть вычислен как S → = A − 1I →, где A — матрица, строки которой являются векторами Стокса анализатора. Регистрация изображения и поляриметрическая калибровка выполняются одновременно с помощью метода, зависящего от угла (дополнительный текстовый раздел S4) ( 17 ).
В поляризационном изображении S → = [S0 S1 S2 S3] T известно в каждом пикселе, что не позволяет легко визуализировать. Вместо этого изображения могут быть сформированы из скалярных величин, полученных из вектора Стокса. В литературе по поляризационной визуализации обычно используются два параметра эллипса поляризации. Первый — это азимутальный угол arctan (S2 / S1), который определяет физическую ориентацию эллипса поляризации. Второй — это степень поляризации, определяемая как p = S12 + S22 + S32 / S0, которая количественно определяет степень, в которой свет (или не является) полностью поляризованным.Наконец, изображение может быть сформировано только из S0, которая, как интенсивность света, дает традиционную монохромную фотографию.
На рис. 4 показаны типичные фотографии, снятые системой поляризационного изображения. Для каждого показаны изображения первичного захвата на датчике, S0, азимутальный угол и степень поляризации (DOP). На всех этих изображениях освещающий свет неполяризован и рассеян, то есть падает со всех сторон. Изображения внутри помещения на рис. 4 получены при рассеянном освещении светодиодами, тогда как изображения на открытом воздухе получены при ярком дневном свете.На необработанных снимках яркий диск в центре представляет свет нулевого порядка, который не взаимодействует с решеткой и, таким образом, формирует расфокусированную версию изображения (также присутствует некоторый рассеянный свет).
Рис. 4 Поляризационные изображения полного Стокса.Фотосъемка в помещении (от A до C ) и вне помещения ( D и E ) с помощью камеры, изображенной на рис. 3. В каждом случае необработанная необработанная экспозиция, S0 (традиционное монохромное изображение яркости), показаны азимут эллипса поляризации [в градусах, заданных как arctan (S2 / S1)], и степень поляризации (DOP, заданные как S12 + S22 + S32 / S0).См. Текст для подробностей по каждому случаю. Изображения в помещении были получены с выдержками порядка 100 мс, изображения на открытом воздухе — с выдержками порядка 10 мс. В обоих случаях поляризационные изображения могут быть получены с частотой кадров видео. Яркий диск в центре каждой необработанной экспозиции — это свет нулевого порядка, который не взаимодействует с решеткой и, таким образом, формирует расфокусированное изображение сцены. Все изображения имеют один цвет (зеленый, λ∼532 нм).
Далее мы опишем каждый пример. На рисунке 4A представлен простой тест — бумажная рамка, содержащая восемь листов поляризационной пленки, оси которой расположены радиально наружу, а свет, формирующий изображение, может проходить сзади.Традиционная фотография не видит разницы между листами (S0), но изображение азимута точно показывает их угловую ориентацию. Более того, изображение DOP показывает, что свет, проходящий через листы, сильно поляризован относительно окружающей поверхности.
На рис. 4, от B до E, исследуется поляризационная зависимость зеркального отражения ( 47 ). Неполяризованный свет становится частично поляризованным при зеркальном отражении в направлении, перпендикулярном плоскости падения.На рис. 4В изображена обычная пластиковая бутылка из-под газировки в лоб. По изображению яркости (S0) изогнутая форма бутылки не может быть определена апостериори. Однако азимутальное изображение демонстрирует плавное, непрерывное изменение вокруг верха бутылки, свидетельствующее о ее конической форме, и может быть использовано в трехмерной (3D) реконструкции; действительно, поляризованная природа зеркального отражения использовалась как средство получения изображения глубины ( 47 — 50 ). Рисунок 4C иллюстрирует ту же концепцию для более сложного объекта — лица одного из авторов.Его трехмерная природа не различима на изображении S0 (в отличие, скажем, от простой печатной фотографии лица), но азимутальное изображение отслеживает его контур и может использоваться в трехмерной реконструкции лица.
На рисунках 4, D и E изображены сцены на открытом воздухе. На рис. 4D на территории Гарвардского кампуса после дождя виден велосипед, припаркованный на травянистом поле. Перед ним граница между травой и асфальтом, а также лужа. На азимутальном изображении видно четкое очертание между мокрым покрытием, где направление поляризации четко определено параллельно земле, и травой и лужей, где азимут несколько случайен, потому что отражение диффузное.Кроме того, азимут показывает наличие асфальтовой дорожки в задней части изображения, которую трудно увидеть на изображении интенсивности. На рис. 4E сфотографирован ряд автомобилей. Освещенные солнечным светом автомобили — излюбленная цель в литературе по поляризационным изображениям, потому что ветровые стекла имеют тенденцию давать сильные поляризационные сигнатуры. Это видно для всех трех автомобилей на азимутальном изображении, где лобовые стекла и кузова автомобилей имеют определенные азимуты поляризации, и на изображении DOP, где лобовые стекла сильно поляризованы относительно остальной части автомобиля и фона.
Отметим, однако, что примеры на рис. 4 лишь косвенно используют S3, киральную стоксову компоненту, через ДОП. Многие существующие поляризационные камеры, особенно использующие метод разделения фокальной плоскости, не могут измерять S3 ( 42 ). Рисунок 5, однако, прямо демонстрирует возможности камеры в режиме полного Стокса. На рис. 5 объекты освещаются сзади светом с линейной поляризацией под 45 ° от жидкокристаллического дисплея компьютера. В каждом случае показаны необработанные данные датчика, S0 и S3.На рисунке 5A изображена пара 3D-очков, оправы которых содержат противоположные круговые поляризаторы. Это не видно на традиционном изображении интенсивности S0, но хорошо видно на изображении S3, где каждая линза имеет значение ± 1. На рис. 5B кусок акрила удерживается перед камерой, показывая небольшой хиральный компонент. После сжатия (рис. 5C) на традиционной фотографии не заметно никаких изменений, но теперь на S3 видна значительная информация, обусловленная двойным лучепреломлением под напряжением (фотоупругий эффект).Это также очевидно на рис. 5D, где пластиковая деталь, отлитая под давлением, — дозатор ленты — демонстрирует встроенное сложное распределение напряжений в S3, не видимое при традиционной фотографии. Визуализация полей напряжений — важное применение поляризационного изображения, которое легко выполняется с помощью представленной здесь камеры.
Рис. 5 Поляризационное изображение S3.Пример изображения с камеры, явно использующей S3, что является частью ее возможностей полного Стокса.Все изображения получены с подсветкой, линейно поляризованной под 45 °. В каждом примере показаны необработанные данные датчика, S0 (традиционное изображение яркости) и S3. ( A ) Видно, что 3D-очки содержат противоположные круговые поляризаторы, невидимые для традиционного изображения яркости. ( B и C ) Акриловая деталь, вырезанная лазером, подвергается сжатию вручную и демонстрирует двойное лучепреломление напряжения, очевидное на изображении S3. ( D ) Пластиковая деталь, изготовленная литьем под давлением (диспенсер ленты), имеет сложные внутренние напряжения, которые видны в канале S3 поляризационного изображения.Краевые артефакты на этих изображениях и на рис. 4 обсуждаются в дополнительном тексте (раздел S4) ( 17 ).
Эти примеры демонстрируют мощные приложения в области машинного зрения, дистанционного зондирования и других областях. Представленная здесь камера не требует традиционной поляризационной оптики, обеспечивает одновременный сбор данных без движущихся частей, не требует датчика изображения, специально снабженного микрополяризаторами, и является компактной и потенциально производимой в массовом порядке. Более того, простота камеры — всего одна решетка с объективом для формирования изображения — предполагает, что эти решетки могут быть спроектированы вокруг существующих традиционных систем формирования изображений для создания чувствительных к поляризации.
Заключение
Мы ввели общую картину поляризационно-зависимой дифракции на поляризационно-чувствительных препятствиях. Эта матричная фурье-оптика описывает оптические элементы, которые могут выполнять многие поляризационно-зависимые функции в своих дифракционных картинах. В этой работе мы применили это изображение к случаю периодических решеток, анализирующих произвольные поляризации параллельно, охарактеризовали эти решетки и показали, как они позволяют использовать поляризационную камеру без дополнительной поляризационной оптики, движущихся частей или специализированных датчиков.Продемонстрирована практическая поляризационная фотография этой камерой.
Наша работа обобщает большой объем исследований в области поляризационно-чувствительной дифракционной оптики и метаповерхностей. Его акцент делается на коллективном поведении сразу многих элементов, выраженном в преобразовании Фурье, а не на поэтапном рассмотрении каждого элемента в отдельности, и, таким образом, продвигает стратегии проектирования в этих областях за пределы простых фазовых профилей. Кроме того, в данной работе предлагается несколько интересных направлений исследований в области многофункциональной поляризационной оптики.Например, хотя здесь изучались анализаторы поляризации (поляризаторы), матричный подход является довольно общим: решетки реализуют широкий спектр поляризационных операторов на их порядках [например, волновые пластины, оптически активные среды и, возможно, более экзотическое поведение ( 51 ). )] можно было представить. Ограничение линейно двулучепреломляющих элементов ни в коем случае не является фундаментальным, и со свободой, предоставляемой литографическим изготовлением, элементы с более сложными поляризационными откликами ( 52 ) или многослойные структуры могут быть использованы для реализации этого поведения.Эта работа демонстрирует способность метаповерхностей заметно упрощать архитектуру систем, использующих поляризационную оптику. Решетки, обеспечиваемые этим подходом, представляют собой более простые средства формирования изображений с полной стоксовой поляризацией, которые можно легко распространить на другие системы формирования изображений и с другими длинами волн. Эти компактные, легкие и пассивные устройства могут обеспечить широкое распространение поляризационной визуализации.
Ссылки и примечания
- ↵
- ↵
- ↵
- ↵
L.Николова, П. Рамануджам, Поляризационная голография (Cambridge Univ. Press, 2009).
- ↵
- ↵
- ↵
- ↵
- ↵
Дж. У. Гудман, Введение в Фурье-оптику (Робертс, 2005).
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵См. Дополнительные материалы.
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵ 90↵13 905
- ↵
- ↵
- ↵
- ↵
- ↵
F.Snik et al ., Proceedings of the SPIE 9099 (2014).
- ↵
- ↵
- ↵
- ↵
S. Rahmann, N. Canterakis, in Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (2001), pp. 155.
А. Кадамби, В. Таамазян, Б. Ши, Р. Раскар, Proc. Международная конференция IEEE по компьютерному зрению (2015 г.), стр.3370–3378.
- ↵
- ↵
- ↵
- ↵
F. Gori, Diffractive Optics and Optical Microsystems , S. Martellucci, A. N. Chester, Eds. (Springer, 1997), стр. 3–22.
Дж. Н. Дамаск, Поляризационная оптика в телекоммуникациях (Springer, 2005).
R. A. Chipman, W.-S. Лам, Дж. Янг, Поляризованный свет и оптические системы (CRC Press, 2019).
- ↵
р.Э. Якобсен, Г. Г. Аттридж, С. Ф. Рей, Н. Р. Аксфорд, Руководство по фотографии: фотографические и цифровые изображения (Focal Press, 2000)
Gaussian Optics — документация SymPy 1.8
Гауссова оптика.
В модуле реализовано:
Матрицы передачи лучей для геометрической и гауссовой оптики.
См. RayTransferMatrix, GeometricRay и BeamParameter
Соотношения сопряжения для геометрической и гауссовой оптики.
См. Geometry_conj *, gauss_conj и contugate_gauss_beams
Условные обозначения для расстояний следующие:
- фокусное расстояние
позитив для собирающих линз
- расстояние до объекта
положительное для реальных объектов
- расстояние до изображения
позитив для реальных изображений
- класс
sympy.физика.оптика.гауссопт.BeamParameter( wavelen , z , z_r = None , w = None ) [источник] Представление гауссова луча в формализме матрицы передачи лучей.
- Параметры
wavelen : длина волны,
z : расстояние до талии, а
w : талия, или
зір : релейный ряд.
Примеры
>>> из sympy.physics.optics import BeamParameter >>> p = BeamParameter (530e-9, 1, w = 1e-3) >>> p.q 1 + 1.88679245283019 * I * pi
>>> p.q.n () 1.0 + 5.92753330865999 * Я >>> p.w_0.n () 0,00100000000000000 >>> p.z_r.n () 5.92753330865999
>>> из sympy.physics.optics import FreeSpace >>> fs = FreeSpace (10) >>> p1 = fs * p >>> стр.w.n () 0,00101413072159615 >>> p1.w.n () 0,00210803120
- 9
- R606
https://en.wikipedia.org/wiki/Complex_beam_parameter
- R607
https://en.wikipedia.org/wiki/Gaussian_beam
- свойство
расхождение Половина общего углового разброса.
Примеры
>>> из sympy.physics.optics import BeamParameter >>> p = BeamParameter (530e-9, 1, w = 1e-3) >>> p. расхождение 0,00053 / пи
- недвижимость
гоуи Фаза Гуи.
Примеры
>>> из sympy.physics.optics import BeamParameter >>> p = BeamParameter (530e-9, 1, w = 1e-3) >>> стр.гуй атан (0,53 / пи)
- недвижимость
кв Комплексный параметр, представляющий балку.
Примеры
>>> из sympy.physics.optics import BeamParameter >>> p = BeamParameter (530e-9, 1, w = 1e-3) >>> p.q 1 + 1.88679245283019 * I * pi
- недвижимость
радиус Радиус кривизны фазового фронта.2 \) интенсивность.
Примеры
>>> из sympy.physics.optics import BeamParameter >>> p = BeamParameter (530e-9, 1, w = 1e-3) >>> p.w 0,001 * sqrt (0,2809 / пи ** 2 + 1)
См. Также
-
w_0 Минимальный радиус балки.
-
- недвижимость
w_0 Перетяжка балки (минимальный радиус).2 \) интенсивность
Список литературы
- свойство
талия_approximation_limit Минимальная перетяжка, для которой справедливо приближение пучка Гаусса.
Пояснение
Гауссов пучок является решением параксиального уравнения. Для искривлений которые слишком велики, это не верное приближение.
Примеры
>>> из sympy.physics.optics import BeamParameter >>> p = BeamParameter (530e-9, 1, w = 1e-3) >>> стр.талия_approximation_limit 1.06e-6 / pi
- класс
sympy.physics.optics.gaussopt.CurvedMirror( R ) [источник] Матрица переноса лучей для отражения от изогнутой поверхности.
- Параметры
R : радиус кривизны (положительный для вогнутости)
Примеры
>>> от sympy.Physics.optics импорт CurvedMirror >>> из символов импорта sympy >>> R = символы ('R') >>> Изогнутое зеркало (R) Матрица ([ [1, 0], [-2 / R, 1]])
- класс
sympy.physics.optics.gaussopt.CurvedRefraction( R , n1 , n2 ) [источник] Матрица переноса лучей для преломления на изогнутой поверхности раздела.
- Параметры
R:
Радиус кривизны (положительный для вогнутого).
n1:
Показатель преломления одной среды.
№2:
Показатель преломления другой среды.
Примеры
>>> из sympy.physics.optics import CurvedRefraction >>> из символов импорта sympy >>> R, n1, n2 = символы ('R n1 n2') >>> CurvedRefraction (R, n1, n2) Матрица ([ [1, 0], [(n1 - n2) / (R * n2), n1 / n2]])
- класс
sympy.физика.оптика.гауссопт.FlatMirror[источник] Матрица передачи лучей для отражения.
Примеры
>>> from sympy.physics.optics import FlatMirror >>> FlatMirror () Матрица ([ [1, 0], [0, 1]])
- класс
sympy.physics.optics.gaussopt.FlatRefraction( n1 , n2 ) [источник] Матрица передачи лучей для преломления.
- Параметры
n1:
Показатель преломления одной среды.
№2:
Показатель преломления другой среды.
Примеры
>>> from sympy.physics.optics import FlatRefraction >>> из символов импорта sympy >>> n1, n2 = символы ('n1 n2') >>> FlatRefraction (n1, n2) Матрица ([ [1, 0], [0, n1 / n2]])
- класс
sympy.физика.оптика.гауссопт.FreeSpace( d ) [источник] Матрица передачи лучей для свободного места.
- Параметры
расстояние
Примеры
>>> из sympy.physics.optics import FreeSpace >>> из символов импорта sympy >>> d = символы ('d') >>> FreeSpace (d) Матрица ([ [1, д], [0, 1]])
- класс
sympy.физика.оптика.гауссопт.GeometricRay( * args ) [источник] Представление геометрического луча в формализме матрицы переноса лучей.
- Параметры
h : высота и
угол : угол, или
матрица : матрица 2×1 (Матрица (2, 1, [высота, угол]))
Примеры
>>> от sympy.Physics.optics импорт GeometricRay, FreeSpace >>> из символов импорта sympy, матрица >>> d, h, angle = символы ('d, h, angle')>>> GeometricRay (h, угол) Матрица ([ [h], [угол]])
>>> FreeSpace (d) * GeometricRay (h, угол) Матрица ([ [угол * d + h], [ угол]])
>>> GeometricRay (Матрица (((h,), (угол,)))) Матрица ([ [h], [угол]])
- свойство
угол Угол с оптической осью.
Примеры
>>> из sympy.physics.optics импортировать GeometricRay >>> из символов импорта sympy >>> h, angle = symbols ('h, angle') >>> gRay = Геометрический луч (h, угол) >>> gRay.angle угол
- недвижимость
высота Расстояние от оптической оси.
Примеры
>>> от sympy.Physics.optics импорт GeometricRay >>> из символов импорта sympy >>> h, angle = symbols ('h, angle') >>> gRay = Геометрический луч (h, угол) >>> gRay.height час
- класс
sympy.physics.optics.gaussopt.RayTransferMatrix( * args ) [источник] Базовый класс для матрицы передачи лучей.
Его следует использовать, если не указан более конкретный подкласс в См. также.
- Параметры
параметры:
A, B, C и D или матрица 2×2 (Matrix (2, 2, [A, B, C, D]))
Примеры
>>> из sympy.physics.optics импортировать RayTransferMatrix, ThinLens >>> из sympy import Symbol, Matrix
>>> mat = RayTransferMatrix (1, 2, 3, 4) >>> мат Матрица ([ [1, 2], [3, 4]])
>>> RayTransferMatrix (Матрица ([[1, 2], [3, 4]])) Матрица ([ [1, 2], [3, 4]])
>>> f = символ ('f') >>> линза = тонкая линза (f) >>> объектив Матрица ([ [1, 0], [-1 / f, 1]])Список литературы
- R608
https: // en.wikipedia.org/wiki/Ray_transfer_matrix_analysis
- недвижимость
А Параметр A матрицы.
Примеры
>>> из sympy.physics.optics импортировать RayTransferMatrix >>> mat = RayTransferMatrix (1, 2, 3, 4) >>> мат.А 1
- недвижимость
Б Параметр B матрицы.
Примеры
>>> из sympy.physics.optics импортировать RayTransferMatrix >>> mat = RayTransferMatrix (1, 2, 3, 4) >>> мат.B 2
- недвижимость
C Параметр C матрицы.
Примеры
>>> из sympy.physics.optics импортировать RayTransferMatrix >>> mat = RayTransferMatrix (1, 2, 3, 4) >>> мат.C 3
- недвижимость
D Параметр D матрицы.
Примеры
>>> из sympy.physics.optics импортировать RayTransferMatrix >>> mat = RayTransferMatrix (1, 2, 3, 4) >>> мат.D 4
- класс
sympy.physics.optics.gaussopt.ThinLens( f ) [источник] Матрица переноса лучей для тонких линз.
- Параметры
Факс:
Примеры
>>> from sympy.physics.optics import ThinLens >>> из символов импорта sympy >>> f = символы ('f') >>> Тонкие линзы (е) Матрица ([ [1, 0], [-1 / f, 1]])
-
sympy.physics.optics.gaussopt.conugate_gauss_beams( wavelen , Waist_in , Waist_out , ** kwargs ) [источник] Найдите оптическую схему, соединяющую талию объекта / изображения.
- Параметры
wavelen:
Длина волны луча.
до талии_внутри и_вытяжки:
Спряжение талии.
ф:
Фокусное расстояние элемента, используемого в сопряжении.
- Возвращает
кортеж, содержащий (s_in, s_out, f)
s_in:
Расстояние до оптического элемента.
s_out:
Расстояние после оптического элемента.
ф:
Фокусное расстояние оптического элемента.
Примеры
>>> из sympy.physics.optics импортировать конъюгат_гаусс_beams >>> из символов импорта sympy, фактор >>> l, w_i, w_o, f = символы ('l w_i w_o f')>>> conugate_gauss_beams (l, w_i, w_o, f = f) [0] е * (1 - sqrt (w_i ** 2 / w_o ** 2 - pi ** 2 * w_i ** 4 / (f ** 2 * l ** 2)))
>>> фактор (конъюгированные_гауссы (l, w_i, w_o, f = f) [1]) f * w_o ** 2 * (w_i ** 2 / w_o ** 2 - sqrt (w_i ** 2 / w_o ** 2 - пи ** 2 * w_i ** 4 / (f ** 2 * l ** 2))) / w_i ** 2>>> conugate_gauss_beams (l, w_i, w_o, f = f) [2] ж
-
sympy.физика.оптика.гауссопт.gaussian_conj( s_in , z_r_in , f ) [источник] Соотношение сопряжения для гауссовых пучков.
- Параметры
s_in:
Расстояние до оптического элемента от талии.
z_r_in:
Рэлеевский диапазон падающего луча.
ф:
Фокусное расстояние оптического элемента.
- Возвращает
кортеж, содержащий (s_out, z_r_out, m)
s_out:
Расстояние между новой перетяжкой и оптическим элементом.
z_r_out:
Рэлеевский диапазон выходящего пучка.
м:
Соотношение между новой и старой талией.
Примеры
>>> от sympy.Physics.optics импорт gaussian_conj >>> из символов импорта sympy >>> s_in, z_r_in, f = символы ('s_in z_r_in f')>>> gaussian_conj (s_in, z_r_in, f) [0] 1 / (- 1 / (s_in + z_r_in ** 2 / (- f + s_in)) + 1 / f)
>>> gaussian_conj (s_in, z_r_in, f) [1] z_r_in / (1 - s_in ** 2 / f ** 2 + z_r_in ** 2 / f ** 2)
>>> gaussian_conj (s_in, z_r_in, f) [2] 1 / sqrt (1 - s_in ** 2 / f ** 2 + z_r_in ** 2 / f ** 2)
-
sympy.физика.оптика.гауссопт.geometry_conj_ab( a , b ) [источник] Соотношение сопряжения геометрических балок в параксиальных условиях.
Пояснение
Измеряет расстояния до оптического элемента и возвращает необходимое фокусное расстояние.
Примеры
>>> из sympy.physics.optics import geometry_conj_ab >>> из символов импорта sympy >>> a, b = символы ('a b') >>> geometry_conj_ab (a, b) а * б / (а + б)
-
sympy.физика.оптика.гауссопт.geometry_conj_af( a , f ) [источник] Соотношение сопряжения геометрических балок в параксиальных условиях.
Пояснение
Измеряет расстояние до объекта (для geometry_conj_af) или расстояние до изображения (для geometry_conj_bf) к оптическому элементу и фокусному расстоянию. Затем он возвращает другое расстояние, необходимое для сопряжения.
Примеры
>>> от sympy.Physics.optics.gaussopt импорт геометрической_conj_af, геометрической_conj_bf >>> из символов импорта sympy >>> a, b, f = символы ('a b f') >>> geometry_conj_af (a, f) а * ф / (а - е) >>> geometry_conj_bf (b, f) б * ж / (б - ж)
-
sympy.physics.optics.gaussopt.geometry_conj_bf( a , f ) [источник] Соотношение сопряжения геометрических балок в параксиальных условиях.
Пояснение
Измеряет расстояние до объекта (для geometry_conj_af) или расстояние до изображения (для geometry_conj_bf) к оптическому элементу и фокусному расстоянию. Затем он возвращает другое расстояние, необходимое для сопряжения.
Примеры
>>> из sympy.physics.optics.gaussopt import geometry_conj_af, geometry_conj_bf >>> из символов импорта sympy >>> a, b, f = символы ('a b f') >>> geometry_conj_af (a, f) а * ф / (а - е) >>> geometry_conj_bf (b, f) б * ж / (б - ж)
-
sympy.физика.оптика.гауссопт.rayleigh3waist( z_r , wavelen ) [источник] Рассчитайте перетяжку из диапазона Рэлея гауссова пучка.
Примеры
>>> from sympy.physics.optics import rayleigh3waist >>> из символов импорта sympy >>> z_r, wavelen = symbols ('z_r wavelen') >>> rayleigh3waist (z_r, wavelen) sqrt (wavelen * z_r) / sqrt (пи)
-
sympy.физика.оптика.гауссопт.traffic2rayleigh( w , wavelen ) [источник] Вычислите диапазон Рэлея от перетяжки гауссова пучка.
Примеры
>>> from sympy.physics.optics import Waist2rayleigh >>> из символов импорта sympy >>> w, wavelen = символы ('w wavelen') >>> талия2рейли (ш, вейвлен) пи * ш ** 2 / волна
Трассировка лучей и матричная оптика ABCD, Eugene Hecht, Chpt скачать на ppt
Презентация на тему: «Трассировка лучей и матричная оптика ABCD», Евгений Хехт, гл.6. «- стенограмма презентации:
ins [data-ad-slot = «4502451947»] {display: none! important;}} @media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}} @media (max-width: 800px) {# place_14 {width: 250px;}} @media (max-width: 500 пикселей) {# place_14 {width: 120px;}} ]]>1 Трассировка лучей и матричная оптика ABCD, Евгений Хехт, гл.6
2 Основы трассировки лучей Рассмотрим 2D-проекцию Луч однозначно определяется положением и углом — Составьте компоненты вектора Параксиальная аппроксимация — Выразите угол как наклон = y ’ = y’ y z
3 Пример: расстояние распространения L Угол (наклон) без изменений Положение зависит от исходного положения и наклона (y 0, y 0 ’) (y 1, y 1’)
4 Пример: пройти через линзу. Положение не изменилось. Изменение угла (наклона) зависит от положения и фокусного расстояния (y 0, y 0 ’) (y 1, y 1’)
5 Матрица ABCD Обобщить Можно каскадом создать единую матрицу для системы Пример: пройти через линзу и распространить расстояние L = f (y 0, y 0 ’) (y 1, y 1’) (y 2, y 2 ’)
6 Пример: преобразование Фурье Распространение расстояния f, прохождение через линзу, распространение f Замена положения и угла — примечание масштабные коэффициенты f и -1 / f (y 0, y 0 ‘) (y 1, y 1’) (y 2, y 2 ‘) (y 3, y 3’) ff
7 Пример — 4 f изображение Каскад в предыдущем примере (y 0, y 0 ‘) (y 1, y 1’) (y 2, y 2 ‘) (y 3, y 3’) ff (y 4, y 4 ‘) (y 5, y 5 ‘) (y 6, y 6’) ff
8 Пример — диэлектрическая граница раздела Закон Снеллиуса — изменение угла, фиксированное положение n1n1 n2n2
9 Другие примеры Легко сгенерировать матрицы ABCD Линза GRIN
10 Оптический резонатор Условие стабильной полости Возврат в исходное состояние после целого числа N циклических обходов
PH-230 Матричная оптика и аберрации
Курс, префикс, номер и название: Матричная оптика и аберрации PH-230
Часы (Класс, декламация, лаборатория, студия): 1 лекционный час, 1 декламация / лабораторный час
Кредиты: 1
Предварительные условия (при наличии): PH-229
Описание курса в каталоге колледжа:
Разделы матричной оптики, применяемые к геометрической (лучевой) оптике, включая распространение луча, тонкие и толстые линзы и системы линз.Введение в аберрации в оптических системах, как они формируются и контролируются.
Академические программы, для которых данный курс является обязательным или факультативным:
A.S. Технические науки
A.A. Свободные искусства и науки
Результаты обучения студентов по курсу:
ИксРезультаты для конкретной программы
ИксМетоды оценки и оценки обучения студентов; описать типы используемых методов; отметьте, требуются ли определенные методы для всех разделов:
Икс Политика академической честности (факультет или колледж):
От всех студентов ожидается академическая честность.Любое нарушение академической честности воспринимается крайне серьезно. Все задания и проекты должны быть оригинальной работой студента или товарищей по команде. Плагиат недопустим. Любые вопросы относительно академической честности должны быть доведены до сведения преподавателя. Ниже приводится Политика Куинсборо общественного колледжа в отношении академической честности: «Официальная политика колледжа заключается в том, что обо всех действиях или попытках, которые являются нарушением академической честности, сообщать в Управление по делам студентов.По усмотрению преподавателя и с согласия участвующего студента или студентов, некоторые случаи, о которых сообщается в Управление по делам студентов, могут быть разрешены в рамках курса и кафедры. Преподаватель имеет право корректировать оценку нарушителя по своему усмотрению, в том числе ставить F за задание или упражнение или, в более серьезных случаях, F студенту за весь курс ». Ознакомиться с политикой университета в отношении академической честности открывается в новое окно (PDF).
Инвалиды
Любой учащийся, который считает, что ему или ей может потребоваться приспособление в связи с воздействием инвалидности, должен связаться с офисом обслуживания студентов с ограниченными возможностями в Научном корпусе, комната S-132, 718-631-6257, чтобы согласовать разумные приспособления для студентов. с документально подтвержденной инвалидностью. Вы можете посетить веб-сайт Службы для студентов с ограниченными возможностями.
Информационный век в оптике: Измерение матрицы пропускания
- Эльберт Г.ван Путтен и Аллард П. Моск
- Комплексные фотонные системы, факультет науки и технологий и Институт нанотехнологий MESA +, Университет Твенте, P.O. Box 217, 7500 AE Enschede, Нидерланды
& bullet; Physics 3, 22
Прохождение света через неупорядоченную среду подробно описывается с помощью высокоразмерной матрицы. Теперь исследователи измерили эту матрицу пропускания напрямую, предоставив новый подход к управлению распространением света.
Рисунок 1: Два оптических элемента полностью характеризуются своей матрицей передачи, которая связывает фронт падающей волны с переданным. В случае тонкой линзы трансформация волнового фронта описывается матрицей 2 × 2, оперирующей вектором, описывающим кривизну волнового фронта [27]. Для более сложных элементов, таких как кубик сахара, матрица передачи работает на основе поперечных мод, что очень велико. Полное знание матрицы пропускания позволяет неупорядоченным материалам фокусировать свет как линзы.Два оптических элемента полностью характеризуются своей матрицей пропускания, которая связывает фронт падающей волны с переданным. В случае тонкой линзы преобразование волнового фронта описывается матрицей 2 × 2, работающей над вектором d … Показать еще Рисунок 1: Два оптических элемента полностью характеризуются своей матрицей пропускания, которая связывает фронт падающей волны с прошедшим. В случае тонкой линзы трансформация волнового фронта описывается матрицей 2 × 2, оперирующей вектором, описывающим кривизну волнового фронта [27].Для более сложных элементов, таких как кубик сахара, матрица передачи работает на основе поперечных мод, что очень велико. Полное знание матрицы пропускания позволяет неупорядоченным материалам фокусировать свет как линзы. ×Оптические элементы, такие как линзы и поляризаторы, используются для изменения распространения света. Преобразования фронта оптической волны, выполняемые этими элементами, описываются простыми и понятными матрицами передачи (рис. 1). Формализм матриц пропускания также используется для микроскопического описания пропускания через более сложные оптические системы, включая непрозрачные материалы, такие как слой краски, в котором сильно рассеивается свет.Для микроскопического описания этого процесса рассеяния требуется матрица пропускания с огромным количеством элементов. Себастьян Попофф, Жоффруа Лероузи, Реми Карминати, Матиас Финк, Клод Боккара и Сильвен Гиган из Института Ланжевена в Париже теперь сообщают в Physical Review Letters об экспериментальном подходе к микроскопическому измерению матрицы пропускания света [1]. Знание матрицы передачи обещает более глубокое понимание транспортных свойств и позволяет точно контролировать распространение света через сложные фотонные системы.
На первый взгляд непрозрачные неупорядоченные материалы, такие как бумага, краска и биологические ткани, полностью отличаются от линз и других прозрачных оптических элементов. В неупорядоченных материалах вся информация во фронте волны, кажется, теряется из-за многократного рассеяния. Распространение света в таких материалах очень успешно описывается диффузионным подходом, в котором отбрасывается информация о фазе и учитывается только интенсивность. Важный признак того, что фазовая информация очень важна в неупорядоченных системах, было дано наблюдением слабой локализации фотонов в диффузионных образцах [2,3].Даже очень длинные световые пути конструктивно интерферируют в точном направлении обратного рассеяния — эффект интерференции, который можно наблюдать почти во всех системах многократного рассеяния. Помехи в сочетании с очень сильным рассеянием даже остановят диффузию, если для локализации Андерсона созданы подходящие условия [4]. Поскольку световые волны не теряют своих свойств когерентности даже после тысяч событий рассеяния, перенос света через неупорядоченный материал вовсе не диссипативный, а когерентный с высокой информационной емкостью [5].
Распространяющаяся монохроматическая световая волна характеризуется формой волнового фронта. Выбрав подходящий базис, падающий на образец волновой фронт может быть разложен на ортогональные моды. Типичным выбором для этого базиса мод являются ортогональные моды волновода или базис плоских волн в свободном пространстве. Поскольку необходимо учитывать только распространяющиеся волны, количество мод конечно, и они составляют основу, в которой записывается матрица передачи. Матрица передачи выборки определяет амплитуду переданного поля для каждой комбинации падающего и переданного режимов.С теоретической точки зрения матрицы передачи являются полезными инструментами для понимания корреляций в переносе света и других волн. Глубокое понимание свойств матрицы передачи было получено в рамках теории мезоскопического переноса [6]. Матрица пропускания играла менее важную роль в экспериментах из-за ее чрезвычайно высокой размерности: это матрица комплексных чисел N × N, где N представляет количество мод падающего (и прошедшего) светового поля, связанного с образцом.Каждая падающая мода соответствует дискретному углу падения, а количество разрешаемых дискретных углов составляет N = 2π A / λ2 [7], где A — площадь освещенной поверхности, λ — длина волны, а коэффициент 2 учитывает две ортогональные поляризации. Следовательно, образец размером 1 мм2 имеет около миллиона поперечных оптических мод. До недавнего времени измерение матрицы с соответствующим большим количеством элементов было за пределами технологических возможностей. Прогресс в технологии создания цифровых изображений теперь позволяет измерять и обрабатывать такие большие объемы данных.В частности, пространственные модуляторы света — управляемые компьютером элементы, которые контролируют фазу в каждом пикселе двумерного волнового фронта — в настоящее время совершают цифровую революцию в оптике и составляют основу эксперимента Попоффа и его коллег.
В своем эксперименте они использовали пространственный модулятор света для точного управления волновым фронтом монохроматического лазерного луча, что позволило им адресовать различные падающие моды сильно разупорядоченного образца. Умело используя часть проходящего света в качестве опорной фазы, они смогли получить информацию об амплитуде и фазе на двумерной матрице ПЗС размером 16 × 16 пикселей.Благодаря этому параллельному обнаружению они измерили 164 элемента матрицы передачи всего за 162 шага. Их метод позволяет глубже охарактеризовать перенос света через мутную среду, что позволяет им контролировать распространение света, как они продемонстрировали, превратив свой образец в элемент фокусировки и обнаружения. Чтобы сфокусировать свет, они использовали информацию в матрице пропускания для построения волновых фронтов, которые после рассеяния образцом формировали плотный фокус. Их подход более гибкий, чем эксперименты с «непрозрачной линзой» первого поколения [8], поскольку данные для создания фокуса в любом желаемом положении уже находятся в матрице передачи.Для обнаружения объектов, помещенных перед рассеивающим образцом, они сравнивали передаваемое поле с информацией, хранящейся в матрице передачи.
Прямой доступ к отдельным элементам матрицы позволяет выполнять статистический анализ по ним. Статистические свойства матрицы передачи описываются с помощью теории случайных матриц, аналитического подхода, который фокусируется на симметриях и законах сохранения, а не на подробных взаимодействиях (введение см.[9] и ссылки в нем). Например, элементы матрицы передачи коррелированы из-за того, что ни один из элементов матрицы или сингулярных значений не может быть больше единицы, поскольку в этом случае будет передаваться более 100% падающей мощности [10]. Однако эта корреляция неуловима и может быть обнаружена только при измерении полной матрицы передачи.
В текущих экспериментах количество измеренных матричных элементов впечатляет (65536), но матрица пропускания всей площади образца еще больше.Тем не менее, матрица, измеренная Popoff et al. был достаточно большим, чтобы проверить важное базовое предсказание теории случайных матриц: гистограмма его сингулярных значений должна иметь своеобразную форму четверти круга [11,12]. Тот факт, что данные следуют этому закону четверти круга, означает, что элементы матрицы существенно не коррелированы, что является хорошим показателем того, что экспериментальная процедура не вводит ложных корреляций. Измеряя матрицы значительно большего размера, можно выявить внутренние корреляции.В достаточно большой матрице распределение сингулярных значений будет отклоняться от закона четверти круга и сходиться к бимодальному распределению, состоящему в основном из полностью передающих (открытых) и полностью отражающих (закрытых) каналов (обзоры см. В [13–15]). ]). Используя информацию в такой матрице, можно будет создать идеальный волновой фронт, который соединяется только с открытыми каналами и передается через непрозрачную среду на все 100%.
Еще один интересный эксперимент будет заключаться в измерении матрицы пропускания образцов с крайним беспорядком.Когда трехмерные образцы приближаются к порогу локализации Андерсона, матрицы пропускания дадут прямое представление о локализованном режиме, в котором моды проходящего света должны обладать интригующими свойствами [13,16–19]. Точно так же было бы чрезвычайно интересно изучить матрицу пропускания так называемого стекла Леви [20], в котором свет распространяется по сильно измененному закону диффузии, или фотонных кристаллов, которые имеют неизбежный беспорядок [21] в дополнение к сложная ленточная структура.
В относительно прозрачных материалах матрица пропускания может использоваться для получения томографической реконструкции образца [22], которая может использоваться для отслеживания процессов внутри живых клеток. Пока не ясно, можно ли распространить этот подход на материалы с более сильным рассеиванием, но есть надежда, что информация может быть получена из непрозрачной биологической ткани [23,24]. Алгоритмы получения информации о скрытых целях из ультразвуковых измерений (см., Например, [25]) могут быть перенесены в оптику.
Подход Попоффа и его коллег знаменует собой начало увлекательного пути к более глубокому пониманию легкого транспорта. Технологический прогресс позволит измерять все большие и большие матрицы, которые содержат всю доступную информацию об образцах. Постоянные разработки в области анализа случайных матриц (см., Например, [26]) позволят разобраться в этих огромных объемах информации. Когда информация в матрице передачи полностью известна, любая неупорядоченная система становится качественным оптическим элементом (рис.1). С технологической точки зрения это имеет большие перспективы: вполне возможно, что неупорядоченные рассеивающие материалы скоро станут предпочтительными нанооптическими элементами.
Ссылки
- S. M. Popoff, G. Lerosey, R. Carminati, M. Fink, A.C.Boccara, S. Gigan, Phys. Rev. Lett. 104 , 100601 (2010)
- M. P. van Albada, A. Lagendijk, Phys. Rev. Lett. 55 , 2692 (1985)
- П. Э. Вольф, Г. Марет, Phys. Rev. Lett. 55 , 2696 (1985)
- А.Lagendijk, B. van Tiggelen, D. S. Wiersma, Phys. Сегодня 62 , № 8, 24 (2009)
- Скипетров С.Е., Phys. Ред. E 67 , 036621 (2003)
- C. W. J. Beenakker, Rev. Mod. Phys. 69 , 731 (1997)
- Р. П. Фейнман, Р. Б. Лейтон и М. Сэндс, Лекции Фейнмана по физике , Vol. 3 (Аддисон-Уэсли, Нью-Йорк, 1965) [Amazon] [WorldCat]
- И. М. Веллекоп, А. П. Моск, Опт. Lett. 32 , 2309 (2007)
- стр.J. Forrester, N. C. Snaith и J. J. M. Verbaarschot, J. Phys. A 36 , R1 (2003)
- J. Pendry, A. MacKinnon, A. Pretre, Physica A 168 , 400 (1990)
- В. А. Марченко и Л. А. Пастур, Math. СССР-Сборник 1 , 457 (1967)
- Э. П. Вигнер, SIAM Rev. 9 , 1 (1967)
- Дж. Пендри, Физика 1 , 20 (2008)
- Дж. Миллер, Phys. Сегодня 61 , № 9, 20 (2008)
- C. W. J. Beenakker, arXiv: 0904.1432 (2009)
- C. M. Soukoulis, E. N. Economou, Phys. Rev. Lett. 52 , 565 (1984)
- А.А. Чабанов, М. Стойчев, А.З. Генак, Nature 404 , 6780 (2000)
- М. Штёрцер, П. Гросс, К. М. Эгертер и Г. Марет, Phys. Rev. Lett. 96 , 063904 (2006)
- S. Faez, A. Strybulevych, J. H. Page, A. Lagendijk, B.A. van Tiggelen, Phys. Rev. Lett. 103 , 155703 (2009)
- П. Бартелеми, Дж. Бертолотти и Д.S. Wiersma, Nature 453 , 495 (2008)
- A. F. Koenderink, A. Lagendijk, W. L. Vos, Phys. Ред. B 72 , 153102 (2005)
- W. Choi et al. , Нац. Методы 4 , 717 (2007)
- З. Якуб, Д. Псалтис, М. С. Фельд и К. Ян, Nature Photon. 2 , 110 (2008)
- И. М. Веллекоп, Э. Г. ван Путтен, А. Лагендейк, А. П. Моск, Опт. Экспресс 16 , 67 (2008)
- М. Финк, Phys. Сегодня 50 , No.3, 34 (1997)
- А. Эдельман и Н. Радж Рао, Acta Numerica 14 , 233 (2005)
- Х. Когельник и Т. Ли, Proc. IEEE 54 , 1312 (1966)
Об авторах
Эльберт ван Путтен работает над докторской степенью. в группе сложных фотонных систем Института нанотехнологий MESA + Университета Твенте в Нидерландах. Его исследования направлены на получение активного контроля над распространением света в сильно неупорядоченных материалах.
Аллард Моск — доцент группы комплексных фотонных систем Института нанотехнологий MESA + Университета Твенте в Нидерландах. Он получил докторскую степень. в 1999 году из Амстердамского университета, где он проводил экспериментальные исследования квантовых газов.

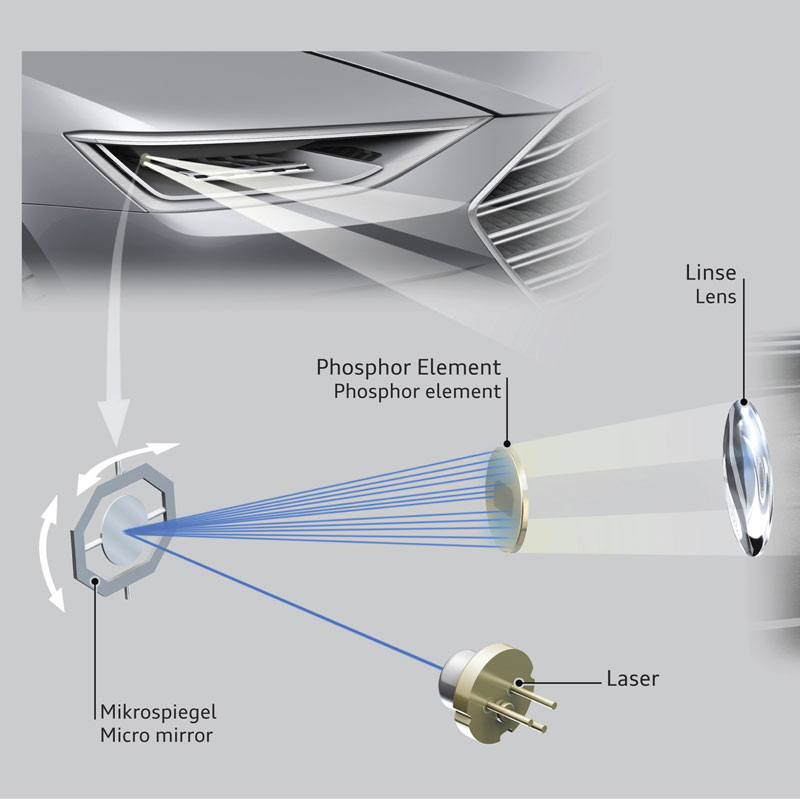 152 — С. 3 — 12 — Тир. 500 экз. Тудоровский А. И. Объектив с фазовой пластинкой Оптика и спектроскопия
152 — С. 3 — 12 — Тир. 500 экз. Тудоровский А. И. Объектив с фазовой пластинкой Оптика и спектроскопия П. Грибковским он провёл расчёт зависимости
П. Грибковским он провёл расчёт зависимости Выделяют
Выделяют В микроскопах встречаются механизмы
В микроскопах встречаются механизмы Все эти достижения встретились в
Все эти достижения встретились в