Коэффициент жесткости пружины
Рано или поздно при изучении курса физики ученики и студенты сталкиваются с задачами на силу упругости и закон Гука, в которых фигурирует коэффициент жесткости пружины. Что же это за величина, и как она связана с деформацией тел и законом Гука?
Блок: 1/7 | Кол-во символов: 250
Источник: https://LivePosts.ru/articles/education-articles/fizika/kak-najti-koeffitsient-zhyostkosti-pruzhiny-formula-opredelenie
Определение и свойства
Коэффициент упругости по определению равен силе упругости, делённой на изменение длины пружины: Коэффициент упругости зависит как от свойств материала, так и от размеров упругого тела. Так, для упругого стержня можно выделить зависимость от размеров стержня (площади поперечного сечения и длины ), записав коэффициент упругости как Величина называется модулем Юнга и, в отличие от коэффициента упругости, зависит только от свойств материала стержня.
Блок: 2/6 | Кол-во символов: 478
Источник: https://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82_%D1%83%D0%BF%D1%80%D1%83%D0%B3%D0%BE%D1%81%D1%82%D0%B8
Типы пружин
Пружины можно классифицировать по направлению прилагаемой нагрузки:
- пружины растяжения; предназначены для работы в режиме растягивания, при деформации их длина увеличивается; как правило, такие устройства имеют нулевой шаг, т.е. намотаны «виток к витку»; примером могут служить пружины в весах-безменах, пружины для автоматического закрытия дверей и т.д.;
- пружины сжатия под нагрузкой, напротив, укорачиваются; в исходном состоянии между их витками есть некоторое расстояние, как, например, в амортизаторах автомобильных подвесок.
В данной статье рассматриваются пружины, представляющие собой цилиндрические спирали. В технике применяется много других разновидностей упругих устройств: пружины в виде плоских спиралей (используются в механических часах), в виде полос (рессоры), пружины кручения (в точных весах), тарельчатые (сжимающиеся конические поверхности) и т.
Блок: 2/5 | Кол-во символов: 1113
Источник: https://spravochnick.ru/fizika/zhestkost_pruzhiny_formula/
Определение и формула жесткости пружины
При рассмотрении того, что такое коэффициент жесткости пружины следует уделить внимание понятию упругости. Для ее обозначения применяется символ F. При этом сила упругости пружины характеризуется следующими особенностями:
- Проявляется исключительно при деформации тела и исчезает в случае, если деформация пропадает.
- При рассмотрении, что такое жесткость пружины следует учитывать, после снятия внешней нагрузки тело может восстанавливать свои размеры и форму, частично или полностью. В подобном случае деформация считается упругой.
Не стоит забывать о том, что жесткость – характеристика, свойственная упругим телам, способным деформироваться. Довольно распространенным вопросом можно назвать то, как обозначается жесткость пружины на чертежах или в технической документации. Чаще всего для этого применяется буква k.
Слишком сильная деформация тела становится причиной появления различных дефектов. Ключевыми особенностями можно назвать следующее:
- Деталь может сохранять свои геометрические параметры при длительной эксплуатации.
- При увеличении показателя существенно снижается сжатие пружины под воздействие одинаковой силы.
- Наиболее важным параметром можно назвать коэффициент жесткости. Он зависит от геометрических показателей изделия, типа применяемого материала при изготовлении.
Довольно большое распространение получили красные пружины и другого типа. Цветовое обозначение применяется в случае производства автомобильных изделий. Для расчета применяется следующая формула: k=Gd 4 /8D 3 n. В этой формуле указываются нижеприведенные обозначения:
- G – применяется для определения модуля сдвига.
Стоит учитывать, что это свойство во многом зависит от применяемого материала при изготовлении витков. - d – диаметральный показатель проволоки. Она производится путем проката. Этот параметр указывается также в технической документации.
- D – диаметр создаваемых витков при накручивании проволоки вокруг оси. Он подбирается в зависимости от поставленных задач. Во многом диаметр определяет то, какая нагрузка оказывается для сжатия устройства.
- n – число витков. Этот показатель может варьировать в достаточно большом диапазоне, также влияет на основные эксплуатационные характеристики изделия.
Стоит учитывать, что это свойство во многом зависит от применяемого материала при изготовлении витков.Рассматриваемая формула применяется в случае расчета коэффициента жесткости для цилиндрических пружин, которые устанавливаются в самых различных механизмах. Подобная единица измеряется в Ньютонах. Коэффициент жесткости для стандартизированных изделий можно встретить в технической литературе.
Блок: 2/7 | Кол-во символов: 2525
Источник: https://MyTooling.ru/instrumenty/vyvod-opredelenie-zhestkosti-pruzhiny
Физические характеристики пружин
Цилиндрические пружины характеризуются рядом параметров, сочетание которых обуславливает их жесткость — способность сопротивляться деформации:
- материал; пружины чаще всего изготавливают из стальной проволоки, причем сталь в них применялася особая, ее характеризует среднее или высокое содержание углерода, низкое содержание других примесей (низколегированный сплав) и особая термообработка (закалка), придающая материалу дополнительную упругость;
- диаметр проволоки; чем он меньше, тем эластичнее пружина, но тем меньше ее способность запасать энергию; пружины сжатия изготавливают, как правило, из более толстой проволоки, чем пружины растяжения;
- форма сечения проволоки; не всегда проволока, из которой намотана пружина, имеет круглое сечение; уплощенное сечение имеют пружины сжатия, чтобы при максимальном сокращении длины (виток «садится» на соседний виток) конструкция была более устойчивой;
- длина и диаметр пружины; длину пружины следует отличать от длины проволоки, из которой она намотана; эти два параметра согласуются через количество витков и диаметр пружины, который, в свою очередь, не следует путать с диаметром проволоки.
Существуют и другие физические характеристики, влияющие на работоспособность пружин. Например, при повышении температуры металл становится менее упругим, а при существенном ее понижении может стать хрупким. При интенсивной эксплуатации пружина со временем теряет часть упругости по причине постепенного разрушения связей между атомами кристаллической решетки.
Источник: https://spravochnick.ru/fizika/zhestkost_pruzhiny_formula/
Расчет пружины сжатия из проволоки прямоугольного сечения
Жесткость пружины из проволоки или прутка прямоугольного сечения при тех же габаритах, что и из круглой проволоки может быть гораздо больше. Соответственно и сила сжатия пружины может быть больше.
Основным отличием в расчете, как вы уже догадались, является определение жесткости витка (C 1 ) , задающей жесткость пружины (C ) в целом.
Далее представлены скриншот программы и формулы для цилиндрической стальной пружины из прямоугольной проволоки, у которой поджаты по ¾ витка с каждого конца и опорные поверхности отшлифованы на ¾ длины окружности.
Внимание!!!
После выполнения расчета по программе выполняйте проверку касательных напряжений!!!
4. I =(D 1 / B ) -1
5. При 1/3: Y =5,3942*(H / B ) 2 -0,3572*(H /B )+0,5272
При 1: Y =5,4962*(H / B ) (-1.715)При 2H / B : Y =3 ,9286 *(H / B ) (-1. 2339 )
6. При H B : C 1 =(78500* H 4 )/(Y * (D 1 — B ) 3)
При H > B : C 1 =(78500* B 4 )/(Y * (D 1 — B ) 3)
8.
T nom =1,25*(F 2 / C 1 )+H
9. T max =π*(D 1 — B )*tg (10 ° )
11. S 3 = T — H
12. F 3 = C 1 *
14. N расч =(L 2 — H )/(H +F 3 / C 1 — F 2 / C 1 )
16. C = C 1 / N
17. L 0 = N * T + H
18. L 3 = N * H + H
19. F 2 = C * L 0 — C * L 2
21. F 1 = C * L 0 — C * L 1
22. N 1 = N +1,5
23. A =arctg (T /(π *(D 1 — H )))
24. L разв =π* N 1 *(D 1 — H )/cos (A )
25. Q =H *B * L разв *7,85/10 6
Блок: 3/6 | Кол-во символов: 1488
Источник: https://svetvam.ru/diy/formula-udlineniya-pruzhiny-kak-naiti-koefficient-zh-stkosti.html
Жёсткость деформируемых тел при их соединении
Параллельное соединение пружин.
Последовательное соединение пружин.
При соединении нескольких упруго деформируемых тел (далее для краткости — пружин) общая жёсткость системы будет меняться. При параллельном соединении жёсткость увеличивается, при последовательном — уменьшается.
Параллельное соединение
При параллельном соединении пружин с жёсткостями, равными жёсткость системы равна сумме жёсткостей, то есть
Последовательное соединение
При последовательном соединении пружин с жёсткостями, равными общая жёсткость определяется из уравнения:
Блок: 3/6 | Кол-во символов: 601
Источник: https://ru.
wikipedia.org/wiki/%D0%9A%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82_%D1%83%D0%BF%D1%80%D1%83%D0%B3%D0%BE%D1%81%D1%82%D0%B8
Расчет в Excel жесткости витка пружины
Жесткость витка пружины – это «краеугольный камень в фундаменте» расчетов, зависящий лишь от модуля сдвига материала, из которого пружина навита и её геометрических размеров.
C 1 = G * X 4 /(Y *(D 1 — B ) 3 )
В этой формуле:
G – модуль сдвига материала проволоки
Для пружинной стали:
G ≈78500 МПа ±10%
Для пружинной бронзы:
G ≈45000 МПа ±10%
X – минимальный размер сечения проволоки
Для круглой проволоки – это её диаметр:
X = D
Для прямоугольной проволоки:
X = H при H B
X = B при B H
H – высота сечения проволоки в направлении параллельном оси навивки пружины
B – ширина сечения проволоки в направлении перпендикулярном оси навивки пружины
Для круглой проволоки:
H = B = D
D 1 — наружный диаметр пружины
(D 1 — B ) – средний диаметр пружины
Y – параметр жесткости сечения проволоки
Для круглой проволоки:
Y = 8
Для прямоугольной проволоки:
Y = f (H / B )
Что это за функция — f (H / B ) ? В литературе она всегда задана в виде таблицы, что не всегда удобно, особенно для промежуточных значений H / B , которых попросту нет.
Выполним в MS Excel табличных данных в первых двух столбцах аналитическими функциями, разбив для повышения точности табличные значения на три группы.
На графиках, представленных ниже, Excel нашел три уравнения для определения параметра Y при различных значениях аргумента — отношения высоты проволоки к ширине — H / B . Красные точки – это заданные значения из таблицы (столбец №2), черные линии – это графики найденных аппроксимирующих функций. Уравнения этих функций Excel вывел непосредственно на поля графиков.
В таблице в столбце №3 размещены посчитанные по полученным формулам значения параметра жесткости сечения проволоки Y , а в столбцах №4 и №5 — абсолютные Δ абс и относительные Δ отн погрешности аппроксимации.
Как видно из таблицы и графиков полученные уравнения весьма точно замещают табличные данные! Величина достоверности аппроксимации R 2 очень близка к 1 и относительная погрешность не превышает 2,7%!
Применим на практике полученные результаты.
Блок: 2/6 | Кол-во символов: 2101
Источник: https://svetvam.ru/diy/formula-udlineniya-pruzhiny-kak-naiti-koefficient-zh-stkosti.html
Коэффициент жесткости соединений пружин
Приведенный выше показатель коэффициента жесткости детали при параллельном или последовательном соединении определяет многие характеристики соединения. Довольно часто проводится определение тому, чему равно удлинение пружины. Среди особенностей параллельного или последовательного соединения можно отметить нижеприведенные моменты:
- При параллельном подключении удлинение обоих изделий будет равным. Не стоит забывать о том, что оба варианта должны характеризоваться одинаковой длиной в свободном положении. При последовательном показатель увеличивается в два раза.
- Свободное положение – ситуация, в которой деталь находится без прикладывания нагрузки. Именно оно в большинстве случаев учитывается при проведении расчетов.
- Коэффициент жесткости изменяется в зависимости от применяемого способа подсоединения. В случае параллельного соединения показатель увеличивается в два раза, при последовательном уменьшается.
Для проведения расчетов нужно построить схему подключения всех элементов. Основание представлено линией со штриховкой, изделие обозначается схематически, а тело в упрощенном виде. Кроме этого, от упругой деформации во многом зависит кинетическая и другая энергия.
Блок: 4/7 | Кол-во символов: 1218
Источник: https://MyTooling.ru/instrumenty/vyvod-opredelenie-zhestkosti-pruzhiny
Коэффициент жесткости цилиндрической пружины
На практике и в физике довольно большое распространение получили именно цилиндрические пружины. Их ключевыми особенностями можно назвать следующие моменты:
- При создании указывается центральная ось, вдоль которой и действует большинство различных сил.
- При производстве рассматриваемого изделия применяется проволока определенного диаметра. Она изготавливается из специального сплава или обычных металлов. Не стоит забывать о том, что материал должен обладать повышенной упругостью.
- Проволока накручивается витками вдоль оси. При этом стоит учитывать, что они могут быть одного или разного диаметра. Довольно большое распространение получил вариант исполнения цилиндрического типа, но большей устойчивостью характеризуется цилиндрический вариант исполнения, в сжатом состоянии деталь обладает небольшой толщиной.
- Основными параметрами можно назвать больший, средний и малый диаметр витков, диаметр проволоки, шаг расположения отдельных колец.
Не стоит забывать о том, что выделяют два типа деталей: сжатия и растяжения. Их коэффициент жесткости определяется по одной и той же формуле. Разница заключается в следующем:
- Вариант исполнения, рассчитанный на сжатие, характеризуется дальним расположением витков. За счет расстояние между ними есть возможность сжатия.
- Модель, рассчитанная на растяжение, имеет кольца, расположенные практически вплотную. Подобная форма определяет то, что при максимальная сила упругости достигается при минимальном растяжении.
- Также есть вариант исполнения, который рассчитан на кручение и изгиб. Подобная деталь рассчитывается по определенным формулам.
Расчет коэффициента цилиндрической пружины может проводится при использовании ранее указанной формулы. Она определяет то, что показатель зависит от следующих параметров:
- Наружного радиуса колец. Как ранее было отмечено, при изготовлении детали применяется ось, вокруг которой проводится накручивание колец. При этом не стоит забывать о том, что выделяют также средний и внутренний диаметр. Подобный показатель указывается в технической документации и на чертежах.
- Количества создаваемых витков. Этот параметр во многом определяет длину изделия в свободном состоянии. Кроме этого, количество колец определяет коэффициент жесткость и многие другие параметры.
- Радиуса применяемой проволоки. В качестве исходного материала применяется именно проволока, которая изготавливается из различных сплавов. Во многом ее свойства оказывают влияние на качества рассматриваемого изделия.
- Модуля сдвига, который зависит от типа применяемого материала.
Коэффициент жесткости считается одним из наиболее важных параметров, который учитывается при проведении самых различных расчетов.
Блок: 5/7 | Кол-во символов: 2693
Источник: https://MyTooling.ru/instrumenty/vyvod-opredelenie-zhestkosti-pruzhiny
Это соотношение выражает суть закона Гука. А значит, чтобы найти коэффициент жесткостипружины, следует силу растяжения тела разделить на удлинение данной пружины
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества.
Закон Гука может быть обобщен и на случай более сложных деформаций. В технике часто применяются спиралеобразные пружины (рис. 1.12.3). Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.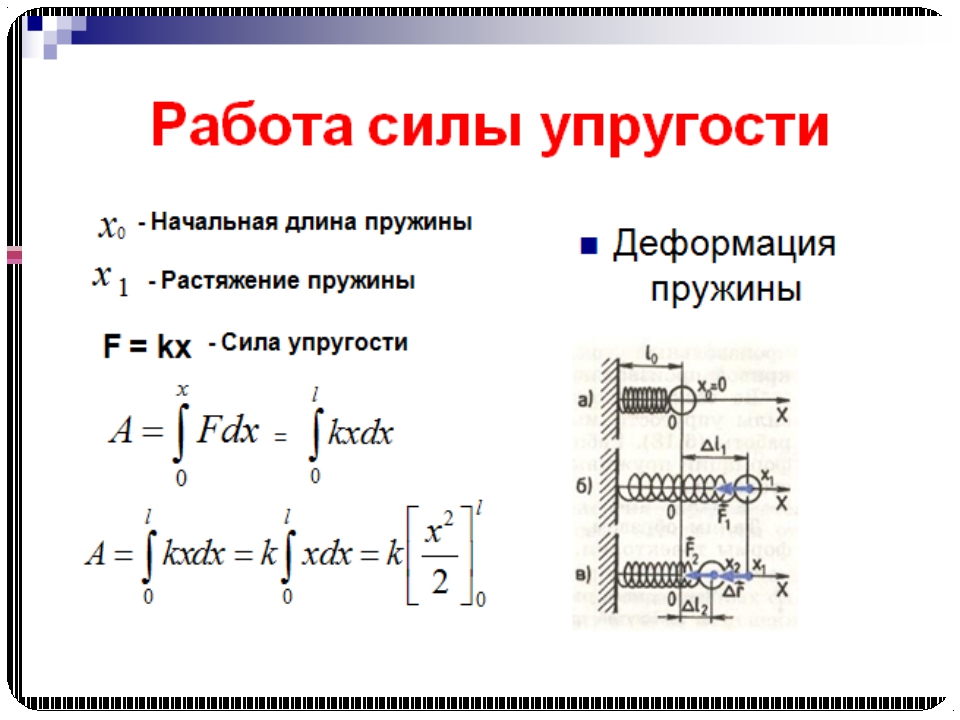
В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Закрепите вертикально один конец пружины, второй же ее конец оставьте свободным. Жесткость – это способность детали или конструкции противодействовать приложенной к нему внешней силе, по возможности сохраняя свои геометрические параметры.
Различные пружины предназначены для работы на сжатие, растяжение, кручение или изгиб. В школе на уроках физики детей учат определять коэффициентжесткости пружины, работающей на растяжение. Для этого на штативе вертикально подвешивается пружина в свободном состоянии.
Вычисление силы Архимеда. Количество теплоты и калориметр. Теплота плавления/кристаллизации и парообразования/конденсации. Теплота сгорания топлива и КПД тепловых двигателей. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).
Поэтому ее часто называют силой нормального давления. Деформация растяжения пружины. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала. С точки зрения классической физики пружину можно назвать устройством, которое накапливает потенциальную энергию путем изменения расстояния между атомами материала, из которого эта пружина сделана.
Блок: 5/6 | Кол-во символов: 2054
Источник: https://svetvam.ru/diy/formula-udlineniya-pruzhiny-kak-naiti-koefficient-zh-stkosti.html
Примеры задач на нахождение жесткости
Задача 1
На пружину длиной 10 см действует сила F = 100 Н. Длина растянутой пружины составила 14 см. Найти коэффициент жесткости.
- Рассчитываем длину абсолютного удлинения: x = 14—10 = 4 см = 0,04 м.
- По формуле находим коэффициент жесткости: k = F/x = 100 / 0,04 = 2500 Н/м.
Ответ: жесткость пружины составит 2500 Н/м.
Задача 2
Груз массой 10 кг при подвешивании на пружину растянул ее на 4 см. Рассчитать, на какую длину растянет ее другой груз массой 25 кг.
- Найдем силу тяжести, деформирующей пружину: F = mg = 10 · 9.8 = 98 Н.
- Определим коэффициент упругости: k = F/x = 98 / 0.04 = 2450 Н/м.
- Рассчитаем, с какой силой действует второй груз: F = mg = 25 · 9.8 = 245 Н.
- По закону Гука запишем формулу для абсолютного удлинения: x = F/k.
- Для второго случая подсчитаем длину растяжения: x = 245 / 2450 = 0,1 м.
Ответ: во втором случае пружина растянется на 10 см.
Блок: 6/7 | Кол-во символов: 919
Источник: https://LivePosts.ru/articles/education-articles/fizika/kak-najti-koeffitsient-zhyostkosti-pruzhiny-formula-opredelenie
Единицы измерения
Основной единицей измерения коэффициента жесткости в системе СИ является:
В СГС:
= дин/см
Блок: 5/6 | Кол-во символов: 128
Источник: http://ru.solverbook.com/spravochnik/koefficienty/koefficient-zhestkosti-pruzhiny/
Видео
Из этого видео вы узнаете, как определить жесткость пружины.
Блок: 7/7 | Кол-во символов: 69
Источник: https://LivePosts.ru/articles/education-articles/fizika/kak-najti-koeffitsient-zhyostkosti-pruzhiny-formula-opredelenie
Особенности расчета жесткости соединений пружин
Приведенная выше информация указывает на то, что коэффициент жесткости является довольно важным параметром, который должен рассчитываться при выборе наиболее подходящего изделия и во многих других случаях. Именно поэтому довольно распространенным вопросом можно назвать то, как найти жесткость пружины. Среди особенностей соединения отметим следующее:
- Провести определение растяжения пружины можно при вычислении, а также на момент теста. Этот показатель может зависеть в зависимости от проволоки и других параметров.
- Для расчетов могут применяться самые различные формулы, при этом получаемый результат будет практически без погрешностей.
- Есть возможность провести тесты, в ходе которых и выявляются основные параметры. Определить это можно исключительно при применении специального оборудования.
Как ранее было отмечено, выделяют последовательный и параллельный метод соединения. Оба характеризуются своими определенными особенностями, которые должны учитываться.
В заключение отметим, что рассматриваемая деталь является важной частью конструкции различных механизмов. Неправильный вариант исполнения не сможет прослужить в течение длительного периода. При этом не стоит забывать о том, что слишком сильная деформация становится причиной ухудшения эксплуатационных характеристик.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Блок: 7/7 | Кол-во символов: 1412
Источник: https://MyTooling.ru/instrumenty/vyvod-opredelenie-zhestkosti-pruzhiny
Количество использованных доноров: 6
Информация по каждому донору:
- https://MyTooling.ru/instrumenty/vyvod-opredelenie-zhestkosti-pruzhiny: использовано 4 блоков из 7, кол-во символов 7848 (42%)
- http://ru.solverbook.com/spravochnik/koefficienty/koefficient-zhestkosti-pruzhiny/: использовано 1 блоков из 6, кол-во символов 128 (1%)
- https://LivePosts.ru/articles/education-articles/fizika/kak-najti-koeffitsient-zhyostkosti-pruzhiny-formula-opredelenie: использовано 3 блоков из 7, кол-во символов 1238 (7%)
- https://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82_%D1%83%D0%BF%D1%80%D1%83%D0%B3%D0%BE%D1%81%D1%82%D0%B8: использовано 2 блоков из 6, кол-во символов 1079 (6%)
- https://spravochnick.ru/fizika/zhestkost_pruzhiny_formula/: использовано 2 блоков из 5, кол-во символов 2643 (14%)
- https://svetvam. ru/diy/formula-udlineniya-pruzhiny-kak-naiti-koefficient-zh-stkosti.html: использовано 3 блоков из 6, кол-во символов 5643 (30%)
ru/diy/formula-udlineniya-pruzhiny-kak-naiti-koefficient-zh-stkosti.html: использовано 3 блоков из 6, кол-во символов 5643 (30%)Жесткость пружины — Энциклопедия по машиностроению XXL
Л4д == /Идо — W (рис. 72, б), где — жесткость пружины, а ф — угол, на который она закручена. [c.132]Для кулачкового механизма 1 вида найти жесткость пружины, обеспечивающей замыкание кинематической пары IV класса [c.228]
Для кулачкового механизма IV вида найти жесткость пружины, замыкающей кинематическую пару IV класса, если ход толкателя Ф = 30 , закон изменения второй производной от функции положения толкателя задан графиком [c.229]
Частота k этого колебания является постоянным параметром для данной установки она зависит от момента инерции колеблющейся системы относительно оси 00, жесткости пружины и в малой степени от сопротивления среды и называется частотой собственных свободных) колебаний системы. [c.297]
Обозначим через х линейную координату перемещения массы М, тогда упругая сила пружины будет —сх, где с — жесткость пружины. Демпфирующие свойства системы представим тоже в виде линейной функции скорости —Ьх. [c.302]
Пружинный двигатель (рис. 4.2) имеет механическую характеристику (рис.4.3, б), аналитическое выражение которой Мд = Мд — —Ф, где — начальное значение момента движущих сил q — жесткость пружины ср — угол закручивания пружины. У электродвигателя постоянного тока механическая характеристика (4.3, в) представляет собой зависимость движущего момента Мд от угловой скорости ротора со Мд = Мд(со). [c.116]
Жесткость пружины с = 20 Н/мм. Длина пружины в свободном состоянии 170 мм, а в предельно сжатом 80 мм. Предварительное поджатие пружины и отвечающее ему перекрытие винтового плунжера = 20 мм.
[c.179]
Жесткость пружины с — 235 Н/мм, ее сжатие I = 2 мм. Диаметр клапана d = 10 мм. Плотность жидкости р == = 900 кг/м . [c.186]
Жесткость пружины с — 7,5 Н/см, длина трубки I = 0,7 м и динамическая вязкость масла р = 0,3 П. Диаметр поршня Л = 30 мм. [c.210]
Жесткость пружины с == 5 Н/см, предварительный натяг Рпр = 25 мм. [c.219]
В данном случае массой груза является масса поршня т плюс масса водяного столба pLF (массой пружины пренебрегаем). Жесткость Со равна жесткости пружины с плюс отнесенное К единице перемещения водяного столба изменение усилия на поршень вследствие изменения напора Hq при колебаниях [c.366]
Пренебрегая массой стержня, определить частоту крутильных колебаний, если масса диска т 1 кг, динамическая вязкость жидкости р = I Пи толщина жидкого слоя Ь = 0,5 мм. Жесткость пружины с = 0,1 Н-м/рад. Течение в вязком слое считать ламинарным. [c.368]
Во избежание несчастных случаев, происходивших от разрыва маховиков, устраивается следующее приспособление. В ободе маховика помещается тело А, удерживаемое внутри его пружиной 5 когда скорость маховика достигает предельной величины, тело А концом своим задевает выступ В задвижки D, которая и закрывает доступ пара в машину. Пусть масса тела А равна 1,5 кг, расстояние е выступа В от маховика равно 2,5 см, предельная угловая скорость маховика 120 об/мин. Определить необходимый коэффициент жесткости пружины с (т. е. величину силы, под действием которой пружина сжимается на 1 см), предполагая, что масса тела А сосредоточена в точке, рас> [c.200]
Предохранительный выключатель паровых турбин состоит из пальца А массы т = 0,225 кг, помещенного в отверстии, просверленном в передней части вала турбины перпендикулярно оси, и отжимаемого внутрь пружиной центр тяжести пальца отстоит от оси вращения вала на расстоянии I = 8,5 мм при нормальной скорости вращения турбины п= 1500 об/мин.
При увеличении числа оборотов на 10% палец преодолевает реакцию пружины, отходит от своего нормального положения на расстояние л = 4,5 мм, задевает конец рычага В и освобождает собачку С, связанную системой рычагов с пружиной, закрывающей клапан парораспределительного механизма турбины. Определить жесткость пружины, удерживающей тело А, т. е. силу, необходимую для сжатия ее на 1 см, считая реакцию пружины пропорциональной ее сжатию.
[c.201]Груз М, подвешенный на пружине к верхней точке А круглого кольца, расположенного в вертикальной плоскости, надает, скользя по кольцу без трения. Найти, какова должна быть жесткость пружины для того, чтобы давление груза на кольцо в нижней точке В равнялось нулю при следующих данных радиус кольца 20 см, масса груза 5 кг, в начальном положении груза расстояние АМ равно 20 см и пружина имеет натуральную длину начальная скорость груза равна нулю массой пружины пренебречь. [c.229]
Определить давление груза М на кольцо в нижней точке В (рисунок предыдущей задачи) при следующих данных радиус кольца 20 см, масса груза 7 кг в начальном положении груза расстояние АМ равно 20 см, причем пружина растянута и длина ее вдвое больше натуральной длины, которая равна 10 см жесткость пружины такова, что она удлиняется на I см при действии силы в 4,9 Н начальная скорость груза равна нулю массой пружины пренебрегаем. [c.229]
Груз М, подвешенный к неподвижной точке А на пружине, совершает малые гармонические колебания в вертикальной плоскости, скользя без трения по дуге окружности, диаметр которой А В равен / натуральная длина пружины я жесткость пружины такова, что при действии силы, равной весу груза М, она получает удлинение, равное Ь. Определить период Т колебаний в том случае, когда I — а А- Ь массой пружины пренебречь и считать, что при колебаниях она остается растянутой. [c.238]
Определить период свободных колебаний груза массы т, прикрепленного к двум параллельно включенным пружинам, п коэффициент жесткости пружины, эквивалентной данной двойной пружине, если груз расположен так, что удлинения обеих пружин, обладающих заданными коэффициентами жесткости С[ и С2, одинаковы.
[c.239]
Определить коэффициент жесткости пружины, эквивалентной трем пружинам, показанным на рисунке, при колебаниях точки М в абсолютно гладких направляющих вдоль оси х. Решить ту же задачу, если направляющие расположены вдоль осп у. Определить частоты этих колебаний. [c.241]
Груз Р массы т подвешен на пружине к концу стержня длины I, который может поворачиваться вокруг оси О. Коэффициент жесткости пружины С]. Пружина, поддерживающая стержень, установлена на расстоянии Ь от точки О и имеет коэффициент жесткости 2. Определить собственную частоту колебаний груза Р. Массой стержня пренебречь. [c.244]
Коэффициенты жесткости пружин С1= = С2 = 1,225 Н/см, коэффициент трения при движении тела / = 0,2, при покое /о = 0,25. В начальный момент тело было отодвинуто от своего среднего положения О вправо в положение хо = 3 см и отпущено без начальной скорости. Найти 1) область возможных равновесных положений тела — область застоя , 2) величину размахов тела, 3) число его размахов, 4) продолжительность каждого из них, 5) положение тела после колебаний. [c.248]
Груз массы 100 г, подвешенный к концу пружины, движется в жидкости. Коэффициент жесткости пружины с = 19,6 Н/м. Сила сопротивления движению пропорциональна первой степени скорости груза Я = аи, где а = 3,5 Н-с/м. [c.250]
Составить дифференциальное уравнение малых колебаний тяжелой точки А, находящейся на конце стержня, закрепленного шарнирно в точке О, считая силу сопротивления среды пропорциональной первой степени скорости с коэффициентом пропорциональности а, и определить частоту затухающих колебаний, Еес точки А равен Р, коэффициент жесткости пружины с, длина стержня , расстояние ОВ = Ь. Массой стержня пренебречь. В положении равновесия стержень горизонтален. При каком значении коэффициента а движение будет апериодическим [c.251]
Составить дифференциальное уравнение малых колебаний точки А и определить частоту затухающих колебаний.
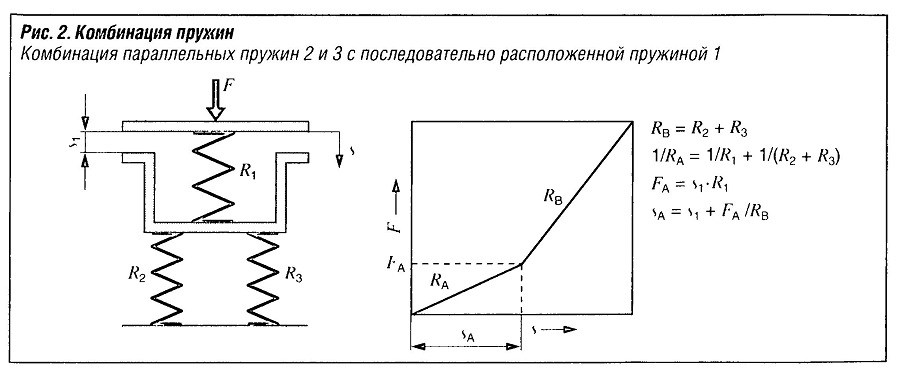Вес точки А равен Р, коэффициент жесткости пружины с, расстояние ОА = Ь, ОВ — I. Сила сопротивления среды пропорциональна первой степени скорости, коэффициент пропорциональности равен
[c.251]В вибрографе для записи горизонтальных колебаний фундаментов машин маятник ОА, состоящий из рычага с грузом на конце, может качаться вокруг своей горизонтальной оси О, удерживаясь в вертикальном положении устойчивого равновесия собственной массой и спиральной пружиной. Определить период собственных колебаний маятника при малых углах отклонения, если максимальный статический момент силы тяжести маятника относительно его оси вращения равен Mgh, момент инерции относительно той же оси равен /г, коэффициент жесткости пружины, сопротивление которой пропорционально углу закручивания, равен с при равновесном положении маятника пружина находится в ненапряженном состоянии. Сопротивлениями пренебречь. [c.287]
Определить угол а, на который повернется ось гироскопа вместе с его рамкой, если прибор установлен на платформе, вращающейся с угловой скоростью 0)1 вокруг оси X, перпендикулярной оси у вращения рамки. Коэффициенты жесткости пружин равны с угол а считать малым расстояние от оси вращения рамки до пружин равно а. [c.313]
Центробежный пружинный регулятор состоит из двух грузов А и В массы М каждый, насаженных на скрепленный со шпинделем регулятора гладкий горизонтальный стержень муфты С массы М , тяг длины / II пружин, отжимающих грузы к оси вращения расстояние шарниров тяг от оси шпинделя равно е с — коэффициент жесткости пружин. Определить угловую скорость регулятора при угле раствора а, если при угле oq, где ао [c.353]
При наезде тележки А на упругий упор В начинаются колебания подвешенного на стержне груза D. Составить дифференциальные уравнения движения материальной системы, если m — масса тележки, тг—масса груза, I—длина стержня, с —коэффициент жесткости пружины упора В. Массой колес и всеми силами сопротивления пренебречь.
Начало отсчета оси х
[c.364]
АВ — ВС и ОЕ = ЕР жесткости пружин с, Сг, Сз, заданы. Бруски АС и ОЕ считать жесткими, не имеющими массы. [c.407]
Определить период колебания груза Р массы т, подвешенного на пружине с закрепленным верхним концом, если коэффициент жесткости пружины равен с, масса пружины /По. Принять, что отношение отклонений двух точек пружины от своих положений равновесия равно отношению соответствующих расстояний этих точек до закрепленного конца пружины. [c.410]
Два одинаковых физических маятника подвешены па параллельных горизонтальных осях, расположенных в одной горизонтальной плоскости, и связаны упругой пружиной, длина которой в ненапряженном состоянии равна расстоянию между осями маятников. Пренебрегая сопротивлением движению и массой пружины, определить частоты и отношения амплитуд главных колебаний системы при малых углах отклонения от равновесного положения. Вес каждого маятника Р радиус инерции его относительно оси, проходящей через центр масс параллельно осп подвеса, р жесткость пружины с, расстояния от центра масс маятника и от точки прикрепления пружины к маятникам до оси подвеса равны соответственно I и Н. ( м. рисунок к задаче 56.4,) [c.418]
Определить частоты главных колебаний двойного математического маятника при условии что массы грузов М1 и М2 соответственно равны ггц и Шг, ОМ1 = /1, М[Мз — /2, а к грузу М1 присоединена пружина, массой которой можно пренебречь. Длина пружины в ненапряженном состоянии равна /э, жесткость пружины с. [c.419]
Пренебрегая трением, определить диаметр клапана ri, н его подъем у, если диаметр дифференциального поршня i/o 15 мм и расход жидкости через клапан Q == 6,3 лУс. Жесткость пружины с = 20,2 Н/мм и ее натяг при у = 0 0 = 5 мм. Коэффнцнеит расхода клапана р = 0,6. Плот- юсть жидкости р =- 900 кгУм . [c.185]
Жесткость пружины с = 20 Н/см начальный Р1атяг пружины при закрытом клапане = 50 мм.
Массой пружины пренебречь.
[c.363]
К одной и той же пружине подвесили сначала груз веса р, а во второй раз груз веса Зр. Определить, во сколько раз изменится период колебаний. Зная коэффициент жесткости пружины с, а также начальные условия (грузы подвешивались к концу церастянутой пружины и отпускались без начальной скорости), найти уравнения движения грузов. [c.236]
Определить коэффициент жесткости эквиваленыгой пружины, если груз М массы т прикреплен к стержню, массой которого можно пренебречь. Стержень шарнирно закреплен в точке О и прикреплен тремя вертикальными пружинами к фундаменту. Коэффициенты жесткости пружин с,, с , Сз. Пружины прикреплены к стержню на расстояниях аь вг, Оз от шарнира. Груз М прикреплен к стержню на расстоянии Ь от шарнира. В положении равновесия стержень горизонтален. Эквивалентная пружина крепится к стержню на расстоянии Ь от шарнира. Найти частоту малых колебаний груза. [c.241]
Цилиндр веса И, радиуса г и высоты Н подвешен на пружине АВ, верхний конец которой В закреплен цилиндр погружен в воду. В положении равновесия цилиндр погружается в воду на половину своей высоты. В начальный момент времени цилиндр был погружен в воду па 2/з своей высоты и затем без начальной скорости пришел в движение по вертикальной прямой. Считая жесткость пружины равной с и предполагая, что действие воды сводится к добавочной архимедовой силе, определить движение цилиндра относительно положения равновесия. [c.247]
Для уменьшения действия на тело массы т возмущающей силы F = Fosin pt + к задаче 32.107 + O) устанавливают пружинный амортизатор с жидкостным демпфером. Коэффициент жесткости пружины с. Считая, что сила сопротивления пропорциональна первой степени скорости (Ясопр = ссо), найти максимальное динамическое давление всей системы на фундамент при установившихся колебаниях.
[c.257]Масса якоря М, общая жесткость пружин с. Самоиндукция катущки изменяется вследствие изменения воздушного зазора в — магпитопроводе 1 — 1 х) х — вертикальное смещение якоря из положения, когда пружины не напряжены). К катущке присоединена электрическая цепь, состоящая из элемента с заданной э. д.с. Е, сопротивление цени равно Я. Составить уравнения движения системы и определить ее положение равновесия. [c.370]
Тяжелый однородный стержень длины I и массы ГП1 риж-иим концом опирается на шарнир и удерживается в вертикальном положении с помощью пружины жесткости с. К точке стержня, отстоящей от щарнира на расстоянии а, подвещен на нити длины г груз М массы П12. При вертикальном положении стержня пружина находится в ненапряженном состоянии и расположена горизонтально. При какой жесткости пружины стержень и груз могут соверщать малые колебания около вертикального положения Найти уравнение частот этих колебаний. Массой нити пренебречь, (иц/ + 2т.2а) [c.424]
I равен О, Полагая коэффициенты жесткости пружин равными С1 = сз = 10О//, определить устойчивость равновесия системы, а также чз9тоты и формы fl и /а главных колебаний системы. /Час-сой пружин пренебречь /1 = /г = /. [c.426]
Сила упругости и закон Гука
☰
Чем большей деформации подвергается тело, тем значительней в нем возникает сила упругости. Это значит, что деформация и сила упругости взаимосвязаны, и по изменению одной величины можно судить об изменении другой. Так, зная деформацию тела, можно вычислить возникающую в нем силу упругости. Или, зная силу упругости, определить степень деформации тела.
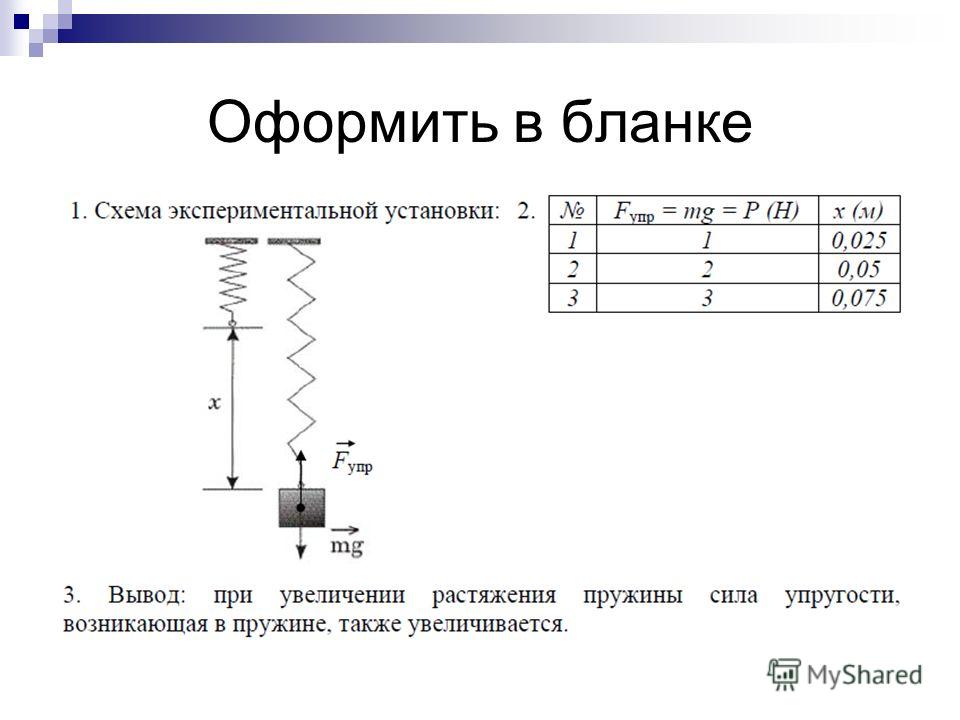
Если к пружине подвешивать разное количество гирек одинаковой массы, то чем больше их будет подвешено, тем сильнее пружина растянется, то есть деформируется. Чем больше растянута пружина, тем большая в ней возникает силы упругости. Причем опыт показывает, что каждая следующая подвешенная гирька увеличивает длину пружины на одну и туже величину.
Так, например, если исходная длина пружины была 5 см, а подвешивание на ней одной гирьки увеличило ее на 1 см (т. е. пружина стала длиной 6 см), то подвешивание двух гирек увеличит ее на 2 см (общая длина составит 7 см), а трех — на 3 см (длина пружины будет 8 см).
Еще до опыта известно, что вес и возникающая под его действием сила упругости находятся друг с другом в прямопропорциональной зависимости. Кратное увеличение веса во столько же раз увеличит силу упругости. Опыт же показывает, что деформация точно также зависит от веса: кратное увеличение веса во столько же раз увеличивает изменения в длине. Это значит, что, исключив вес, можно установить прямопропорциональную зависимость между силой упругости и деформацией.
Если обозначить удлинение пружины в результате ее растяжения как x или как ∆l (l1 – l0, где l0 — начальная длина, l1 — длина растянутой пружины), то зависимость силы упругости от растяжения можно выразить такой формулой:
Fупр = kx или Fупр = k∆l, (∆l = l1 – l0 = x)
В формуле используется коэффициент k. Он показывает, в какой именно зависимости находятся сила упругости и удлинение. Ведь удлинение на каждый сантиметр может увеличивать силу упругости одной пружины на 0,5 Н, второй на 1 Н, а третьей на 2 Н. Для первой пружины формула будет выглядеть как Fупр = 0,5x, для второй — Fупр = x, для третьей — Fупр = 2x.
Коэффициент k называют жесткостью пружины. Чем жестче пружина, тем труднее ее растянуть, и тем большее значение будет иметь k. А чем больше k, тем больше будет сила упругости (Fупр) при равных удлинения (x) разных пружин.
Жесткость зависит от материала, из которого изготовлена пружина, ее формы и размеров.
Единицей измерения жесткости является Н/м (ньютон на метр). Жесткость показывает, сколько ньютонов (сколько сил) надо приложить к пружине, чтобы растянуть ее на 1 м.
Или насколько метров растянется пружина, если приложить для ее растяжения силу в 1 Н. Например, к пружине приложили силу в 1 Н, и она растянулась на 1 см (0,01 м). Это значит, что ее жесткость равна 1 Н / 0,01 м = 100 Н/м.
Также, если обратить внимание на единицы измерения, то станет понятно, почему жесткость измеряется в Н/м. Сила упругости, как и любая сила, измеряется в ньютонах, а расстояние — в метрах. Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них).
Соотношение между силой упругости и деформацией упругого тела, описываемое формулой Fупр = kx, открыл английский ученый Роберт Гук в 1660 году, поэтому это соотношение носит его имя и называется законом Гука.
Упругой деформацией является такая, когда после прекращения действия сил, тело возвращается в свое исходное состояние. Бывают тела, которые почти нельзя подвергнуть упругой деформации, а у других она может быть достаточно большой. Например, поставив тяжелый предмет на кусок мягкой глины, вы измените его форму, и этот кусок сам уже не вернется в исходное состояние. Однако если вы растяните резиновый жгут, то после того, как отпустите его, он вернет свои исходные размеры. Следует помнить, что закон Гука применим только для упругих деформаций.
Формула Fупр = kx дает возможность по известным двум величинам вычислять третью. Так, зная приложенную силу и удлинение, можно узнать жесткость тела. Зная, жесткость и удлинение, найти силу упругости. А зная силу упругости и жесткость, вычислить изменение длины.
Закон Гука и жесткость пружин
Мы анализируем линейные и обратные отношения, содержащиеся в законе Гука.
Закон Гука — это фундаментальное соотношение, объясняющее, как груз на пружине растягивается этой пружиной. Здесь есть фундаментальная прямая пропорциональность с константой пропорциональности, называемой жесткостью пружины \ (\ normalsize {k} \).
Однако, когда мы спрашиваем о соотношении между \ (\ normalsize {k} \) и длиной пружины, мы обнаруживаем обратную пропорциональность! Закон Гука объясняет колебания пружины и связь с круговыми функциями.На этом этапе вы узнаете- о математической форме закона Гука
- о том, как жесткость пружины изменяется в зависимости от длины пружины
- , как колебания пружины являются моделью для гармонического движения.
Закон Гука: восстанавливающая сила пропорциональна смещению
В физике движение колеблющейся пружины является важным колебанием, которое дает знакомые косинусные и синусоидальные круговые функции в виде амплитуд в зависимости от времени. Истоки этого движения лежат в особенно простой линейной зависимости, которую имеют пружины до определенной точки, когда вы их смещаете.© Svjo / Wikimedia Commons «Крюк-закон-пружины» CC BY SA На диаграмме мы видим, что удвоение силы удваивает смещение. Это еще одна формулировка закона Гука. Это было обнаружено британским физиком Робертом Гуком в 1660 году и обозначено как \ [\ Large {F = kx} \], где \ (\ normalsize {F} \) — сила, необходимая для создания смещения \ (\ normalsize { x} \) в положении пружины. (Иногда этот закон появляется с отрицательным знаком и значение силы меняется на противоположное.) Это действительный закон только для относительно небольших значений \ (\ normalsize {x} \), но в этом диапазоне, если вы хотите удвоить смещение , вам нужно удвоить усилие на пружине.В этом случае коэффициент пропорциональности \ (\ normalsize {k} \) зависит от жесткости пружины.
Пример
Предположим, что у нас есть пружина, длина которой естественным образом равна \ (\ normalsize 6 \) см, когда она свободно висит. Если мы поместим на пружину небольшой груз размером \ (\ normalsize 30 \) г, мы заметим, что она растягивается на \ (\ normalsize 2 \) мм. Исходя из этого, мы можем использовать линейную зависимость, чтобы предсказать, какие расширения мы получим с другими массами. Если мы удвоим массу до \ (\ normalsize 60 \) gm, мы ожидаем, что струна растянется вдвое дальше, до \ (\ normalsize 4 \) мм.Если, с другой стороны, мы заменим массу на \ (\ normalsize 10 \) gm, то мы ожидаем, что расширение также уменьшится на треть от того, что было, а именно до \ (\ normalsize 2/3 \) мм.Q1 (E): если масса \ (\ normalsize 10 \) кг на тяжелой промышленной пружине размером \ (\ normalsize 100 \) см создает расширение \ (\ normalsize 3 \) мм, то как большое расширение было бы вызвано \ (\ normalsize 15 \) кг? Какую массу нам придется приложить к исходной пружине, чтобы получить удлинение на \ (\ normalsize 5 \) мм?
Как жесткость пружины зависит от длины?
Но разве мы не обсуждаем обратные отношения? Как мы обсуждали на первой неделе, закон Гука является примером прямой пропорциональности.Но за этим законом стоит другой закон, который является прекрасным примером обратной пропорциональности.
Предположим, у нас есть заданная пружина с заданной жесткостью пружины \ (\ normalsize {k} \). Что произойдет, если мы разрежем эту пружину на две части одинакового размера? Одна из этих более коротких пружин будет иметь новую жесткость пружины, которая будет \ (\ normalsize {2k} \). В более общем смысле, жесткость пружины составляет , обратно пропорциональна длине пружины, предполагая, что мы говорим о пружине из определенного материала и толщины.
Итак, предположим, что мы разрезаем пружину в приведенном выше примере ровно на две части, создавая две более короткие пружины, каждая длиной \ (\ normalsize 3 \) см. Одна из меньших пружин будет иметь жесткость пружины , вдвое превышающую исходную . Это потому, что жесткость пружины и длина пружины обратно пропорциональны. Это означает, что исходная масса \ (\ normalsize 30 \) gm даст только растяжение на \ (\ normalsize 1 \) мм на более короткой пружине. Чем больше жесткость пружины, тем меньше растяжение, создаваемое данной силой.
Надеюсь, это имеет интуитивный смысл — это не должно быть сюрпризом. Если представить исходную пружину как две более короткие пружины, соединенные вместе, то масса \ (\ normalsize 30 \) растягивает обе меньшие пружины на \ (\ normalsize 1 \) мм, давая общее растяжение \ (\ normalsize 2 \) мм.
Для тех, кто физически склонен, с соответствующими единицами измерения в этом случае сила составляет \ (\ normalsize {F = 0.3} \) ньютонов, а исходное смещение составляет \ (\ normalsize {x = 0.002} \) м. Итак, поскольку \ (\ normalsize {F = kx} \), в этих единицах \ (\ normalsize k = \ frac {0.2 \).
Q2 (M): Если заданная сила \ (\ normalsize {F} \) на пружине создает смещение на \ (\ normalsize {8} \) см, мы разрезаем эту пружину на три равных частей, какое усилие нужно приложить к одной из частей, чтобы создать смещение на \ (\ normalsize {4} \) см?
Колебание пружины и гармоническое движение
Особенно простая связь между возвращающей силой и смещением в законе Гука имеет прекрасные последствия для движения колеблющейся пружины.Если вы опустите вес на пружину и отпустите ее, она будет колебаться вокруг своего среднего положения в так называемом гармоническом движении .
Довольно удивительно, но это в точности идентично другому фундаментальному движению: \ (\ normalsize {y} \) — координата частицы, которая движется по единичной окружности равномерно с постоянной скоростью. Если вы посмотрите на эти два примера, надеюсь, вы увидите сходство в движениях.
Причина этого кажущегося совпадения связана с дифференциальными уравнениями, но сводится к относительно простому соотношению закона Гука.
Ответы
A1. Поскольку по закону Гука расширение прямо пропорционально силе, которая для подвешенного груза прямо пропорциональна массе, мы утверждаем, что если масса \ (\ normalsize 10 \) кг создает расширение \ (\ normalsize 3 \) мм, то масса в \ (\ normalsize 15 \) кг вызовет расширение на \ (\ normalsize 4.5 \) мм. Чтобы получить расширение \ (\ normalsize 5 \) мм, нам потребуется масса m, где
\ [\ Large \ frac {10} {m} = \ frac {3} {5}.\]Решая, получаем \ (\ normalsize m = 50/3 = 16,7 \) кг.
A2. Если жесткость пружины изначально равна \ (\ normalsize {k} \), то по закону Гука приложенная сила равна \ (\ normalsize {F = 8k} \). Теперь для одной из меньших частей, мы знаем, что жесткость пружины утроилась, до \ (\ normalsize k_1 = 3k \). Если новая требуемая сила равна \ (\ normalsize {F_1} \), то \ (\ normalsize {F_1 = 4k_1 = 4 (3k)} \). Отсюда следует, что
\ [\ Large {\ frac {F} {F_1} = \ frac {8k} {12k} = \ frac {2} {3}} \]и так \ (\ normalsize {F_1} \) должно быть \ (\ normalsize {\ frac {3} {2}} = 1.В 5 \) раз больше, чем \ (\ normalsize {F} \).
Пружинные постоянные: уравнения и расчеты | Научный проект
F = -kx
Где F — сила, действующая на пружину в Ньютонах (Н),
k — жесткость пружины в Ньютонах на метр (Н / м),
и x — это смещение пружины из положения равновесия.
Жесткость пружины, k , отражает жесткость пружины.Более жесткие (более трудно растягиваемые) пружины имеют более высокие жесткие пружины. Смещение объекта — это измерение расстояния, которое описывает изменение от нормального или равновесного положения.
Рассчитайте жесткость пружины, используя закон Гука.
Как вы думаете, какая пружина будет иметь наибольшую жесткость пружины? Наименьшая жесткость пружины? Почему?
- Весы (измеряют в граммах или килограммах)
- Линейка (сантиметровая)
- Пружины винтовые разные
- Малый вес
- Деревянная доска
- Стол или столешница
- Книги или другие штабелируемые предметы
- С помощью взрослого прикрепите один конец каждой пружины к одной стороне деревянной доски.Обязательно оставляйте пару дюймов между каждой пружиной. Почему нужно фиксировать один конец пружины?
- Разложите книги на столе или столешнице в две стопки по длине деревянной доски.
- Положите деревянную доску на стопки пружинами вниз. Убедитесь, что между нижней частью пружин и столом все еще есть место.
- Используя сантиметровую сторону линейки, измерьте положение равновесия каждой пружины.
- Взвесьте небольшой груз на весах и запишите его массу в килограммах. Почему масса должна быть в килограммах?
- Прикрепите груз по очереди к каждой пружине и с помощью линейки измерьте смещение . Самый простой способ сделать это — измерить длину пружины, а затем вычесть равновесную длину.
- Рассчитайте силу тяжести, действующую на пружину.
F г = мг
Где F g — сила тяжести в Ньютонах, m — масса груза в килограммах, а g — гравитационная постоянная Земли, равная 9.81 м / с 2 .
Установите гравитационную силу ( F, г, , ), равную силе, прилагаемой пружиной ( F) . Почему можно сделать эти две переменные эквивалентными? Используйте закон Гука для расчета жесткости пружины k для каждой пружины.
Пружины с большей жесткостью пружины будут иметь меньшее смещение, чем пружины с меньшей жесткостью пружины при той же добавленной массе.
Закон Гука представляет собой линейную упругую деформацию .Упругость означает, что пружина вернется к своей первоначальной форме после того, как внешняя сила (масса) будет удалена. Линейный описывает соотношение между силой и смещением. Тот факт, что жесткость пружины является постоянной (это свойство самой пружины), показывает, что зависимость является линейной.
Конечно, закон Гука остается верным только тогда, когда материал эластичен. Если пружина необратимо деформирована (например, из-за раздавливания или чрезмерного растяжения), она больше не вернется в исходное положение.Если вы когда-либо играли с обтяжкой и случайно слишком сильно растянули ее или искривили форму, вы поймете, что впоследствии она не работает так, как предполагалось.
Чтобы закон Гука работал правильно, части уравнения должны быть указаны в правильных единицах. Без согласованных единиц уравнение бессмысленно.
Вы можете установить гравитационную силу, прилагаемую массой к пружине, равной силе, прилагаемой к пружине, в соответствии с третьим законом движения Ньютона, который гласит, что силы действуют парами.Каждая сила имеет равную и противоположную силу.
Заявление об отказе от ответственности и меры предосторожностиEducation.com предлагает идеи проекта Science Fair для информационных целей. только для целей. Education.com не дает никаких гарантий или заверений относительно идей проектов Science Fair и не несет ответственности за любые убытки или ущерб, прямо или косвенно вызванные использованием вами таких Информация. Получая доступ к идеям проекта Science Fair, вы отказываетесь от отказаться от любых претензий к Education.com, которые возникают из-за этого. Кроме того, ваш доступ к веб-сайту Education.com и идеям проектов Science Fair покрывается Политика конфиденциальности Education.com и Условия использования сайта, которые включают ограничения об ответственности Education.com.
Настоящим дается предупреждение, что не все идеи проекта подходят для всех индивидуально или при любых обстоятельствах. Реализация идеи любого научного проекта должны проводиться только в соответствующих условиях и с соответствующими родительскими или другой надзор.Прочтите и соблюдайте правила техники безопасности всех Материалы, используемые в проекте, являются исключительной ответственностью каждого человека. За Для получения дополнительной информации обратитесь к справочнику по научной безопасности вашего штата.
Учебное пособие по линейным и нелинейным пружинам
Убедитесь, что в вашем браузере включен JavaScript. Если вы оставите отключенным JavaScript, вы получите доступ только к части предоставляемого нами контента. Вот как.В этом учебном пособии представлен базовый обзор линейных и нелинейных пружин и связанных с ними уравнений силы, жесткости и потенциальной энергии.Вам потребуется базовое понимание исчисления (интегралов и производных), чтобы понять раздел, посвященный нелинейным пружинам.
Определения
Линейная пружина — это пружина с линейной зависимостью между силой и смещением, что означает, что сила и смещение прямо пропорциональны друг другу. График зависимости силы от смещения для линейной пружины всегда будет прямой линией с постоянным наклоном.
Нелинейная пружина имеет нелинейную зависимость между силой и смещением.График, показывающий зависимость силы от смещения для нелинейной пружины, будет более сложным, чем прямая линия с изменяющимся наклоном.
Обзор уравнений
| Линейные пружины | Пружины нелинейные | |
|---|---|---|
| Сила: | [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение] | [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение] |
| Жесткость: | [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение] | [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение] |
| Потенциальная энергия: | [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение] | [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение] |
|
Кредиты
Автор: Бен Финио, доктор философии, приятели науки
Если вы когда-нибудь изучали пружины на уроках физики или где-либо еще, этот символ может быть вам знаком:
Рисунок 1. Общее обозначение пружины
Символ на Рисунке 1 выше выглядит как типичная «спиральная» металлическая пружина (см. Рисунок 2). В реальной жизни пружины бывают самых разных форм и размеров.Однако другие предметы, например резинки, также могут действовать как пружины.
Рис. 2. Слева: несколько спиральных металлических пружин разных размеров (пользователь Wikimedia Commons Batholith, 2011). Справа: резиновые ленты, которые также бывают разных форм и размеров, также могут вести себя как пружины — даже если они не похожи на символ на рисунке 1 выше (пользователь Wikimedia Commons Chenspec, 2011).
Наряду с символом на Рисунке 1 вы могли видеть это уравнение:
Уравнение 1: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
Это уравнение моделирует базовую физику пружины — оно описывает, как пружина проявляет силу, когда вы нажимаете на нее или тянете на нее.Сила ( F ) (в ньютонах) пропорциональна смещению ( x ) (в метрах) пружины — и сила рассчитывается путем умножения смещения на жесткость пружины ( k ) (в ньютонах на метр). Вы также можете услышать постоянную пружины, называемую жесткостью пружины. Важно отметить, что x в Уравнении 1 составляет , а не общей длины пружины — это разница между текущей длиной пружины и ее нейтральной длиной или длиной покоя (эти термины взаимозаменяемы). .Итак, вы также можете увидеть уравнение 1, записанное как:
Уравнение 2: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
(где x — текущая длина пружины, а x 0 — нейтральная длина пружины)
или:
Уравнение 3: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
(где Δx — разница между текущей длиной пружины и ее нейтральной длиной).
Уравнения 1, 2 и 3 означают одно и то же — вам просто нужно следить за тем, как вы определяете x .
Если мы возьмем уравнение 1 и воспользуемся им для построения кривой зависимости силы от смещения для пружины (возьмем k = 100 Н / м), мы получим график на рисунке 3 ниже. Обратите внимание, что кривая зависимости силы от смещения представляет собой прямую линию — поэтому мы называем ее линейной пружиной . Также обратите внимание, что мы можем переставить уравнение 1:
Уравнение 4: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
Перестановка в уравнении 4 говорит нам, что k — это наклон линии на рисунке 3.Итак, если вы можете создать график зависимости силы от смещения для пружины в одном из ваших экспериментов (самый простой способ сделать это — подвесить груз на пружине и измерить его смещение линейкой), и полученная кривая будет линейной, вы можете использовать уравнение 4 для расчета жесткости пружины. Если результирующая кривая , а не прямая линия, вам нужно будет перейти на вкладку «Нелинейные пружины».
Рис. 3. График зависимости силы от смещения ( [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение] ) для линейной пружины с жесткостью пружины k = 100 Н / м.
Вы также можете быть знакомы с уравнением для потенциальной энергии (или PE ), хранящейся в пружине:
Уравнение 5: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
, где опять же, в зависимости от метода выражения переменной x , это также может быть записано как:
Уравнение 6: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
или:
Уравнение 7: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
Но откуда взялось это уравнение? Мы покажем вам, как прийти к уравнению 5 двумя способами — с исчислением и без него.
Без исчисления
Для линейных пружин вы можете рассчитать потенциальную энергию без расчетов. Для этого нам понадобится еще одно общее физическое уравнение:
Уравнение 8: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
Это уравнение говорит, что работа (или W ) (в джоулях), совершаемая силой (или F ), равна произведению этой силы на расстояние ( d ), на котором она действует.Это также означает, что вы можете рассчитать общую проделанную работу и, следовательно, потенциальную энергию, вычислив площадь под кривой сила-смещение — это именно то, что мы имеем на рисунке 3! Мы знаем, что площадь под кривой силы-смещения для линейной пружины всегда будет прямоугольным треугольником, а площадь прямоугольного треугольника равна:
Уравнение 9: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
Итак, для линейной пружины имеем:
Уравнение 10: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
и вот оно что! Вот как вы придете к уравнению 5.Рисунок 4 ниже помогает проиллюстрировать, как вы рассчитываете площадь.
Рис. 4. Площадь под кривой «сила-смещение» для линейной пружины образует прямоугольный треугольник, и площадь этого треугольника используется для расчета потенциальной энергии, запасенной в пружине.
С исчислением
Если вы знакомы с математическим расчетом, то, вероятно, понимаете, что все, что мы сделали в предыдущем разделе, это взяли частный случай интеграла — в данном случае площадь треугольника.В более общем плане мы хотим интегрировать уравнение 8, чтобы получить запасенную потенциальную энергию (это будет полезно в разделе о нелинейных пружинах). Итак, работа, совершаемая с переменной силой F (u) на расстоянии x , составляет:
Уравнение 11: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
, где и — фиктивная переменная, которую мы вставили для расстояния (помните, что использование одной и той же переменной как для пределов интеграла, так и внутри интеграла считается плохой математической формой — это может вызвать у вас проблемы с учителем математического анализа. !).Если мы подставим уравнение 1 сверху в уравнение 11 и заменим W на PE (это можно сделать, потому что, при условии отсутствия потерь на трение, работа, необходимая для растяжения пружины, будет точно равна полученной в результате запасенной потенциальной энергии весной), определяем, что:
Уравнение 12: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
и снова мы пришли к уравнению 5!
В предыдущем разделе рассматриваются линейные пружины, которые подчиняются простой системе уравнений и ведут себя «хорошо».«Однако в реальной жизни пружины могут вести себя иначе. Например, на рисунке 5 показана кривая силы-смещения, которую мы измерили для резинка в проекте Science Buddies, Время выхода: физика движения снаряда катапульты.
В примере на графике показано усилие, необходимое для растяжения резиновой ленты. Требуемая сила сначала резко увеличивается, а затем увеличивается меньше по мере увеличения смещения (образуя выпуклую кривую).
Рисунок 5. Кривая зависимости силы от смещения для резиновой ленты. Эта кривая нелинейная , поэтому она не соответствует уравнению 1.
Вы видите проблему? Это не прямая линия. Это означает, что резиновая лента не соответствует уравнению 1 (в разделе линейных пружин, где F = kx ) для силы как функции смещения — и, следовательно, не будет соответствовать уравнению 5 (в разделе линейных пружин, где PE = 1/2 k x² ) для потенциальной энергии. Резинка ведет себя как нелинейная пружина .Мы можем использовать инструмент аппроксимации кривой, чтобы найти уравнение для линии. В этом случае уравнение для данных на Рисунке 5 выглядит так:
Уравнение 13: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
Как и в разделе линейных пружин, F — сила в ньютонах, а x — смещение от нейтрального положения пружины в метрах. Значения 33,55 и 0,4871 относятся к резиновой ленте из нашего проекта катапульты, поэтому мы можем написать более общую форму этого уравнения с двумя константами, a и p , где a — коэффициент, а p — показатель степени:
Уравнение 14: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
Этот тип уравнения называется степенным законом , потому что переменная x возведена в степень p .Значения a и p будут разными для разных резинок. Однако, , вы не всегда можете предполагать, что нелинейная пружина будет подчиняться степенному закону! Так случилось и в эксперименте с катапультой — есть и другие потенциальные уравнения для кривой зависимости силы от смещения, такие как экспонента , полином или логарифмический . У нас нет места для объяснения этих различных типов кривых здесь — дело в том, что вы всегда должны проводить эксперимент, чтобы создать силу против.кривую смещения для вашей пружины, а затем выясните, какой тип кривой лучше всего подходит для данных.
Теперь обратите внимание, как уравнение 14 выше отличается от уравнения 1 в разделе «Линейные пружины». Поскольку у нас нелинейная пружина, наклон кривой «сила-смещение» не является постоянным. Определение k как «наклон кривой сила-смещение» по-прежнему верно, но теперь это значение может измениться. В общем, вы можете взять производную кривой силы-смещения в любой точке, чтобы найти жесткость (мы больше не называем это «жесткостью пружины», потому что на самом деле это не константа):
Уравнение 15: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
Для резиновой ленты в нашем проекте мы собираемся округлить показатель степени p до ½.Затем мы можем вставить уравнение 13 в уравнение 15, и мы придем к нашему уравнению для жесткости резиновой ленты:
Уравнение 16: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
На рис. 6 показана зависимость жесткости от смещения для этой конкретной резиновой ленты. Обратите внимание на то, как по мере того, как резинка растягивается больше, жесткость уменьшается, а не остается постоянной.Это означает, что резинка на становится слабее , когда вы ее растягиваете.
Примерный график, показывающий жесткость резиновой ленты при ее растяжении. Жесткость сначала резко уменьшается, а затем уменьшается меньше по мере увеличения смещения, образуя вогнутую кривую.
Рис. 6. Кривая зависимости жесткости от смещения для резиновой ленты, которая ведет себя как нелинейная пружина. Жесткость уменьшается с увеличением смещения, вместо того, чтобы оставаться постоянной.
Мы также хотим вычислить потенциальную энергию этой нелинейной пружины. Мы можем использовать общее уравнение:
Уравнение 17: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
Помните, что PE — это потенциальная энергия, а u — фиктивная переменная, которую мы используем для смещения, потому что мы уже используем x в качестве предела интеграла.В случае с нашей резинкой это оценивается как:
.Уравнение 18: [Пожалуйста, включите JavaScript, чтобы просмотреть уравнение]
Обратите внимание на то, как оно сильно отличается от уравнения 5 (из раздела «Линейные пружины»). Помните, что уравнение 18 относится к резиновой ленте, используемой в этом проекте катапульты — для обычной нелинейной пружины вам нужно будет использовать уравнение 17 для расчета потенциальной энергии после того, как вы найдете уравнение для F (x) .
Видео о нашей науке
Постройте винтовку Гаусса | Сделайте самодельную ловушку для мух | Пакет DIY Glitter Surprise с простой схемой |
Механические колебания — Страница 2
Пример 1.
Кольцо радиуса \ (R \) совершает небольшие колебания вокруг точки поворота \ (O \) (рисунок \ (6 \)). Определите период колебаний.Решение.
Рис. 6.Кольцо, подвешенное в точке \ (O, \), представляет собой физический маятник. Период колебаний определяется по формуле
\ [T = 2 \ pi \ sqrt {\ frac {I} {{mga}}}, \]
где \ (I \) — момент инерции кольца относительно его центра, \ (m \) — масса кольца, \ (a \) — расстояние от точки поворота до центра кольца.{\ cancel {2}}}}} {{\ cancel {m} g \ cancel {R}}}}}
= {2 \ pi \ sqrt {\ frac {{2R}} {g}}.}
\]
Пример 2.
Масса подвешена на двух последовательно соединенных пружинах. Жесткость одной пружины в два раза больше, чем у другой: \ ({k_2} = 2 {k_1}. \) Как изменяется период колебаний, если пружины соединены параллельно (рисунок \ (7 \))?Решение.
Рисунок 7.Рассчитаем эквивалентную жесткость в случае последовательного и параллельного соединения пружин.
В случае последовательного соединения сила упругости каждой пружины равна силе тяжести (без учета веса пружин). Общее удлинение — это сумма расширений каждой пружины:
\ [x = {x_1} + {x_2}. \]
Тогда эквивалентная жесткость равна
. \ [
{x = {x_1} + {x_2}, \; \;} \ Rightarrow
{\ frac {F} {k} = \ frac {F} {{{k_1}}}} + \ frac {F } {{{k_2}}}, \; \;} \ Rightarrow
{\ frac {1} {k} = \ frac {1} {{{k_1}}} + \ frac {1} {{{k_2}) }}, \; \;} \ Rightarrow
{k = \ frac {{{k_1} {k_2}}} {{{k_1} + {k_2}}}.}
\]
При параллельном соединении растяжение обеих пружин одинаковое, а общая сила упругости будет равна сумме сил каждой пружины:
\ [{x = {x_1} = {x_2}, \; \; \;} \ kern-0.3pt {F = {F_1} + {F_2}.} \]
Следовательно, эквивалентная жесткость пружин, соединенных параллельно, равна
. \ [
{F = {F_1} + {F_2}, \; \;} \ Rightarrow
{kx = {k_1} {x_1} + {k_2} {x_2} = \ left ({{k_1} + {k_2 }} \ right) x, \; \;} \ Rightarrow
{k = {k_1} + {k_2}.}
\]
Период колебаний последовательно включенных пружин
.\ [{{T_1} = 2 \ pi \ sqrt {\ frac {m} {k}}} = {2 \ pi \ sqrt {\ frac {{m \ left ({{k_1} + {k_2}} \ справа)}} {{{k_1} {k_2}}}},} \]
и в случае параллельного подключения:
\ [{{T_2} = 2 \ pi \ sqrt {\ frac {m} {k}}} = {2 \ pi \ sqrt {\ frac {m} {{{k_1} + {k_2}}}}. } \]
Теперь мы можем узнать, как изменяется период колебаний при переходе от последовательного к параллельному соединению пружин:
\ [{\ frac {{{T_2}}} {{{T_1}}} = \ frac {{\ sqrt {\ frac {1} {{{k_1} + {k_2}}}}}} {{\ sqrt {\ frac {{{k_1} + {k_2}}} {{{k_1} {k_2}}}}}}} = {\ frac {{\ sqrt {{k_1} {k_2}}}} {{{ k_1} + {k_2}}}.2}}} {{{k_1} + 2 {k_1}}}}
= {\ frac {{\ sqrt 2 \ cancel {k_1}}} {{3 \ cancel {k_1}}}}
= {\ frac {{\ sqrt 2}} {3}.}
\]
Пример 3.
Найти коэффициент \ (Q \) осциллятора, если после \ (50 \) колебаний амплитуда смещения уменьшилась вдвое.Решение.
Сначала мы вычисляем логарифмический декремент \ (\ delta. \) По определению, логарифмический декремент пропорционален натуральному логарифму отношения амплитуд \ ({x_0} \) и \ ({x_N} \) двух колебаний. , разделенных точками \ (N \):
\ [\ delta = \ frac {1} {N} \ ln \ frac {{{x_0}}} {{{x_N}}}.\]
В нашем случае это
\ [{\ delta = \ frac {1} {{50}} \ ln 2} \ приблизительно {\ frac {1} {{50}} \ cdot 0,693} = {0,0139.} \]
Тогда добротность системы равна
.\ [{Q = \ frac {\ pi} {\ delta} \ приблизительно \ frac {\ pi} {{0,0139}}} \ приблизительно {227.} \]
30.3: Метод прямой жесткости и глобальная матрица жесткости
Хотя существует несколько методов конечных элементов, мы анализируем метод прямой жесткости здесь, поскольку он является хорошей отправной точкой для понимания формулировки конечных элементов.Сначала рассмотрим простейший из возможных элементов — одномерную упругую пружину, которая может воспринимать только растягивающие и сжимающие силы. Для показанной пружинной системы мы принимаем следующие условия:
- Условие совместимости — соединенные концы (узлы) соседних пружин имеют одинаковые смещения
- Состояние статического равновесия — равнодействующая сила в каждом узле равна нулю
- Основное отношение — которое описывает, как материал (пружина) реагирует на приложенные нагрузки
Модель пружинной системы
Материальное соотношение может быть получено из основного уравнения для упругого стержня, нагруженного в осевом направлении по своей длине:
\ [\ frac {d} {du} (AE \ frac {\ Delta l} {l_0}) + k = 0 \]
\ [\ frac {\ Delta l} {l_0} = \ varepsilon \]
\ [\ frac {d} {du} (AE \ varepsilon) + k = 0 \]
\ [\ frac {d} {du} (A \ sigma) + k = 0 \]
\ [\ frac {dF} {du} + k = 0 \]
\ [\ frac {dF} {du} = -k \]
\ [dF = -kdu \]
Уравнение жесткости пружины связывает узловые смещения с приложенными силами через жесткость пружины (элемента). 2 \ end {bmatrix}
\ begin {Bmatrix} u_2 \ u_3 \ end {Bmatrix}
=
\ begin {Bmatrix} F_2 \\ F_3 \ end {Bmatrix} \]
, так что глобальная матрица жесткости такая же, как полученная непосредственно в уравнении.15:
(Обратите внимание, что для создания глобальной матрицы жесткости путем сборки матриц жесткости элементов, k 22 задается суммой прямых жесткостей, действующих на узел 2, что является критерием совместимости. Также обратите внимание, что косвенные ячейки k ij либо равны нулю (нет передачи нагрузки между узлами i и j), либо отрицательны, чтобы указать силу реакции.)
Для этого простого случая преимущества сборки матриц жесткости элементов (в отличие от получения глобальной матрицы жесткости напрямую) не очевидны.Поэтому мы рассматриваем следующую (более сложную) систему, которая содержит 5 пружин (элементов) и 5 степеней свободы (задачи, представляющие практический интерес, могут иметь десятки или сотни тысяч степеней свободы (и более!)). Поскольку существует 5 степеней свободы, мы знаем, что порядок матрицы равен 5 × 5. Мы также знаем, что он симметричный, поэтому он принимает форму, показанную ниже:
Мы хотим заполнить ячейки, чтобы сгенерировать глобальную матрицу жесткости. По нашим наблюдениям за более простыми системами, например.грамм. Для двух пружинных систем, описанных выше, появляются следующие правила:
- Член в местоположении ii состоит из суммы прямых жесткостей всех элементов, встречающихся в узле i
- Член в местоположении ij состоит из суммы косвенных жесткостей, относящихся к узлам i и j всех элементов, соединяющих узел i с j
- Добавить отрицание для условий реакции (–k ij )
- Добавьте ноль для комбинаций узлов, которые не взаимодействуют
Следуя этим правилам, мы можем сгенерировать глобальную матрицу жесткости:
Этот тип процесса сборки автоматически обрабатывается коммерческими кодами FEM
.Перетащите пружины на место и нажмите «Построить матрицу», затем примените силу к узлу 5.2) = 0 \]
Поскольку определитель [K] равен нулю, он не обратим, а сингулярен. Уникальных решений нет, и {u} не может быть найден. Если это так в вашей собственной модели, вы, вероятно, получите сообщение об ошибке!
пружинных уравнений | Расчетные уравнения пружины
Точная и эффективная конструкция пружины может быть достигнута в современном мире только с использованием компьютерных программ, способных выполнять сотни одновременных вычислений.Ниже приведены лишь некоторые из основных формул, с помощью которых можно получить преимущество при проектировании пружины сжатия. Позвоните нам для помощи в дизайне. Мы можем провести тщательный анализ и помочь вам разработать лучшую пружину для вашего приложения.
Инженерная константа Spring
Рассчитайте жесткость пружины на основе ее геометрии и модуля сдвига.
Пружина инженерной геометрии
Расчет тангажа, угла подъема и высоты сплошной части.
Инженерная сила и напряжение пружины
Рассчитайте максимальное усилие, которое может принять пружина, и напряжение сдвига с учетом поправочного коэффициента Валя.
Инженерные переменные Spring, используемые в формулах расчета
| Диаметр пружинной проволоки | д |
| Внешний диаметр пружины | D внешний |
| Средний диаметр пружины | Д |
| Модуль Юнга материала | E |
| Максимальное усилие в твердом состоянии | F макс. |
| Модуль сдвига материала | г |
| Свободная длина | L бесплатно |
| Длина провода | L провод |
| Сплошная высота | L цельный |
| Максимальный рабочий объем | L деф |
| Максимально возможная нагрузка | L макс. |
| Поправочный коэффициент Валя | Вт |
| Константа пружины | к |
| Активные катушки | n a |
| Всего витков | n t |
| Плотность материала | п. |
| Коэффициент Пуассона материала | в |
| Угол подъема витков пружины | θ |
| Максимальное напряжение сдвига | τ макс |
IRJET-Запрошенная вами страница не найдена на нашем сайте
IRJET приглашает доклады по различным инженерным и технологическим дисциплинам, научным дисциплинам для Тома 8, выпуск 3 (март-2021)
Отправить сейчас
IRJET Vol-8, выпуск 3, Март 2021 г. Публикация продолжается…
Обзор статей
IRJET получил «Импакт-фактор научного журнала: 7,529» за 2020 год.
Проверить здесь
IRJET получил сертификат регистрации ISO 9001: 2008 для своей системы управления качеством.
IRJET приглашает специалистов по различным инженерным и технологическим дисциплинам, научным дисциплинам для Тома 8, выпуск 3 (март-2021 г.)
Отправить сейчас
IRJET Vol-8, выпуск 3, март 2021 г. Публикация продолжается…
Обзор статей
IRJET получил «Импакт-фактор научного журнала: 7,529» за 2020 год.
Проверить здесь
IRJET получил сертификат регистрации ISO 9001: 2008 для своей системы управления качеством.
IRJET приглашает специалистов по различным инженерным и технологическим дисциплинам, научным дисциплинам для Тома 8, выпуск 3 (март-2021 г.)
Отправить сейчас
IRJET Vol-8, выпуск 3, март 2021 г. Публикация продолжается…
Обзор статей
IRJET получил «Импакт-фактор научного журнала: 7,529» за 2020 год.
Проверить здесь
IRJET получил сертификат регистрации ISO 9001: 2008 для своей системы управления качеством.
IRJET приглашает специалистов по различным инженерным и технологическим дисциплинам, научным дисциплинам для Тома 8, выпуск 3 (март-2021 г.)
Отправить сейчас
IRJET Vol-8, выпуск 3, март 2021 г. Публикация продолжается…
Обзор статей
IRJET получил «Импакт-фактор научного журнала: 7,529» за 2020 год.
Проверить здесь
IRJET получил сертификат регистрации ISO 9001: 2008 для своей системы управления качеством.
IRJET приглашает специалистов по различным инженерным и технологическим дисциплинам, научным дисциплинам для Тома 8, выпуск 3 (март-2021 г.)
Отправить сейчас
IRJET Vol-8, выпуск 3, март 2021 г. Публикация продолжается…
Обзор статей
IRJET получил «Импакт-фактор научного журнала: 7,529» за 2020 год.
Проверить здесь
IRJET получил сертификат регистрации ISO 9001: 2008 для своей системы управления качеством.
IRJET приглашает специалистов по различным инженерным и технологическим дисциплинам, научным дисциплинам для Тома 8, выпуск 3 (март-2021 г.)
Отправить сейчас
IRJET Vol-8, выпуск 3, март 2021 г. Публикация продолжается…
Обзор статей
IRJET получил «Импакт-фактор научного журнала: 7,529» за 2020 год.
Проверить здесь
IRJET получил сертификат регистрации ISO 9001: 2008 для своей системы управления качеством.
IRJET приглашает специалистов по различным инженерным и технологическим дисциплинам, научным дисциплинам для Тома 8, выпуск 3 (март-2021 г.)
Отправить сейчас
IRJET Vol-8, выпуск 3, март 2021 г.