Как определить жесткость пружины: формула, как найти, коэффициент, обозначение

Содержание

формула, как найти, коэффициент, обозначение

Определение

Жесткость — способность твёрдого тела, конструкции или её элементов сопротивляться деформации от приложенного усилия вдоль выбранного направления в заданной системе координат.

Сила жесткости — сила, возникающая в теле в результате его деформации и стремящаяся вернуть его в исходное состояние.

От чего зависит жесткость

Жесткость пружины зависит от нескольких параметров:

геометрии пружины;
типа материала;
коэффициента;
срока эксплуатации.

Геометрия пружины

На жесткость витой пружины влияет:

количество витков;
их диаметр;
диаметр проволоки.

Диаметр намотки измеряется от оси пружины. Так как длина проволоки в пружине значительно больше длины упругого стержня, сопротивляемость внешней деформации многократно возрастает.

Волновые пружины состоят из металлических лент, навитых ребром по окружности заданного диаметра.

Их основные геометрические параметры:

количество витков;
количество волн на виток;
сечение ленты.

Тип материала

У каждого материала есть условный предел упругости, характеризующий его способность восстанавливаться после деформации. Если этот предел превышается, в структуре материала возникают необратимые изменения.

Определение

Предел упругости — механическая характеристика материала, показывающая максимальное напряжение, при котором имеют место только упругие, обратимые деформации.

Предел упругости измеряют в паскалях и определяют по формуле:

$\sigma_{у\;}=\;\frac FS$

где F — действие внешней силы на исследуемый образец, приводящее к повреждениям, а S — его площадь.

Кроме предела упругости, существуют такие характеристики упругости материалов, как модули упругости (модуль Юнга) и сдвига, коэффициент жесткости и другие. Все они взаимосвязаны, поэтому, выяснив значение одной из величин с помощью справочной таблицы, можно вычислить другие.

Коэффициент

Определение

Согласно закону Гука, при малой деформации абсолютная величина силы упругости прямо пропорциональна величине деформации.

Эта линейная зависимость описывается формулой:

$F=\;k\;\times\;x$

где k — коэффициент жесткости, а х — величина, на которую сжалась или растянулась пружина.

Примечание

Деформация считается малой в том случае, когда изменение размеров тела значительно меньше его первоначальных размеров.

Срок эксплуатации

Нахождение под напряжением приводит к постепенной необратимой деформации, называемой ослаблением пружины.

Жесткость пружины влияет на срок ее эксплуатации, как и сила воздействия. Конструкторы пружин, предварительно рассчитав эти параметры, проводят тесты на прототипах, прежде чем начать массовое производство. В специальных установках для испытания на усталость материала их сжимают и отпускают определенное количество циклов, отдельно проверяя поведение пружин при максимальной и минимальной нагрузке.

В чем измеряется жесткость

Жесткость пружины в системе СИ измеряется в ньютонах на метр, Н/м. Также встречается единица измерения ньютон на миллиметр, Н/мм. Численно жесткость равна величине силы, изменяющей размер пружины на метр длины.

Как обозначается

Коэффициент жесткости пружины обозначают буквой k.

Коэффициент жесткости пружины

Определение

Коэффициент жесткости — коэффициент, связывающий в законе Гука удлинение упругого тела и возникающую вследствие этого удлинения силу жесткости.

Применяется в механике твердого тела в разделе упругости.

Формула расчета через массу и длину

Используя закон Гука, коэффициент жесткости можно вычислить по формуле:

$k\;=\;\frac Fx$

Чтобы выяснить силу тяжести, воздействующую на пружину, нужно воспользоваться формулой:

$F\;=\;m\;\times\;g$

где m — масса подвешенного на пружине тела, а g — величина свободного ускорения, равная 9,8.

Чтобы найти х, нужно дважды измерить длину пружины и вычислить разницу между этими двумя значениями.

При соединении нескольких пружин общая жесткость системы меняется. Коэффициенты каждой из пружин суммируются при параллельном соединении. При последовательном соединении общая жесткость вычисляется по формуле:

$\frac1k\;=\;(\frac1{k_1}\;+\;\frac1{k_2}\;+\;…\;+\;\frac1{k_n})$

Как можно измерить жесткость

Измерительные приборы

Приборы для испытания пружин на сжатие-растяжение контролируют приложенное усилие с помощью тензометрического датчика, а также изменение их длины, выводя показатели на дисплей. Без специального прибора измерить осевую жесткость можно, используя динамометр и линейку.

Существуют приборы и для измерения поперечной жесткости пружин. Для этого нужно измерить смещение нескольких точек пружины, определив расстояние и угол между ними.

Практическая задача

Самый простой способ измерить жесткость пружины — провести стандартный школьный опыт со штативом и подвешенными на пружине грузиками.

Для измерения осевой жесткости спиральной пружины используют:

штатив, на котором закрепляют пружину;
крючок, который крепят на свободный ее конец;
грузики с известной массой, которые подвешивают на свободный конец пружины;
линейку, чтобы измерить длину пружины с грузом и без груза.

Проведя несколько измерений с грузиками разной массы и вычислив силу тяжести, воздействовавшую на пружину в каждом из них, можно построить график зависимости длины пружины от приложенного усилия и узнать среднее значение коэффициента жесткости.

Альтернативные способы определения жесткости

Жесткость пружины можно определить и через период ее колебания, воспользовавшись формулой:

$Т\;=\;2\mathrm\pi\sqrt{\frac{\mathrm m}{\mathrm k}}$

Или через частоту колебаний по формуле:

$\omega=\;\sqrt{\frac{\mathrm k}{\mathrm m}}$

Проводя опыт с пружиной, закрепленной на штативе, и грузиками с известной массой, можно не измерять длину пружины, а привести ее в колебательное движение и сосчитать количество колебаний в период времени. 3\;\times\;25}\)

$k = 100 \frac Нм$

Жесткость при деформации кручения существенно отличается от жесткости сжатия-растяжения. Предел прочности при кручении у любого материала будет меньше, чем предел прочности при сжатии-растяжении или изгибе. Торсионная жесткость, также называемая крутильной, в системе СИ измеряется в ньютон-метрах на радиан, сокращенно Н-м/рад. Ее можно определить по формуле:

$k\;=\;\frac M\alpha$

где $М$ — крутящий момент, приложенный к телу, а $\alpha$ — угол закручивания тела по оси приложения крутящего момента.

Жесткость пружины, формула

Определение 1

Пружина — упругий объект, целенаправленно подвергающийся сжатию или растяжению, в результате чего может запасать энергию, а затем, при ослабевании внешней деформирующей силы, возвращать ее. Пружины в нормальных условиях не должны подвергаться остаточным (пластическим) деформациям, т.е. таким воздействиям, после которых форма изделия уже не восстанавливается вследствие нарушения структуры их материала.

Типы пружин

Пружины можно классифицировать по направлению прилагаемой нагрузки:

пружины растяжения; предназначены для работы в режиме растягивания, при деформации их длина увеличивается; как правило, такие устройства имеют нулевой шаг, т.е. намотаны «виток к витку»; примером могут служить пружины в весах-безменах, пружины для автоматического закрытия дверей и т.д.;
пружины сжатия под нагрузкой, напротив, укорачиваются; в исходном состоянии между их витками есть некоторое расстояние, как, например, в амортизаторах автомобильных подвесок.

В данной статье рассматриваются пружины, представляющие собой цилиндрические спирали. В технике применяется много других разновидностей упругих устройств: пружины в виде плоских спиралей (используются в механических часах), в виде полос (рессоры), пружины кручения (в точных весах), тарельчатые (сжимающиеся конические поверхности) и т.п. Своего рода пружинами являются амортизирующие изделия из полимерных эластичных материалов, прежде всего резины. Во всех этих устройствах используется один и тот же принцип — запасать энергию упругой деформации и возвращать ее.

Физические характеристики пружин

Цилиндрические пружины характеризуются рядом параметров, сочетание которых обуславливает их жесткость — способность сопротивляться деформации:

материал; пружины чаще всего изготавливают из стальной проволоки, причем сталь в них применялася особая, ее характеризует среднее или высокое содержание углерода, низкое содержание других примесей (низколегированный сплав) и особая термообработка (закалка), придающая материалу дополнительную упругость;

диаметр проволоки; чем он меньше, тем эластичнее пружина, но тем меньше ее способность запасать энергию; пружины сжатия изготавливают, как правило, из более толстой проволоки, чем пружины растяжения;
форма сечения проволоки; не всегда проволока, из которой намотана пружина, имеет круглое сечение; уплощенное сечение имеют пружины сжатия, чтобы при максимальном сокращении длины (виток «садится» на соседний виток) конструкция была более устойчивой;
длина и диаметр пружины; длину пружины следует отличать от длины проволоки, из которой она намотана; эти два параметра согласуются через количество витков и диаметр пружины, который, в свою очередь, не следует путать с диаметром проволоки.

Существуют и другие физические характеристики, влияющие на работоспособность пружин. Например, при повышении температуры металл становится менее упругим, а при существенном ее понижении может стать хрупким. При интенсивной эксплуатации пружина со временем теряет часть упругости по причине постепенного разрушения связей между атомами кристаллической решетки.

Понятие жесткости

Определение 2

Жесткость как физическая величина характеризует силу, которую нужно приложить к пружине для достижения определенной степени растяжения или сжатия.

Коэффициент жесткости рассчитывается по формуле Гука:

$F = -k \cdot x$,

где $F$ — сила, развиваемая пружиной, $k$ — коэффициент жесткости, зависящий от ее характеристик (см. выше) и измеряемый в ньютонах на метр, $x$ — абсолютное приращение расстояния, на которое изменилась длина пружины после приложения внешней силы. Знак минус в правой части формулы свидетельствует о том, что сила, порождаемая пружиной, действует в противоположном по отношению к нагрузке направлении.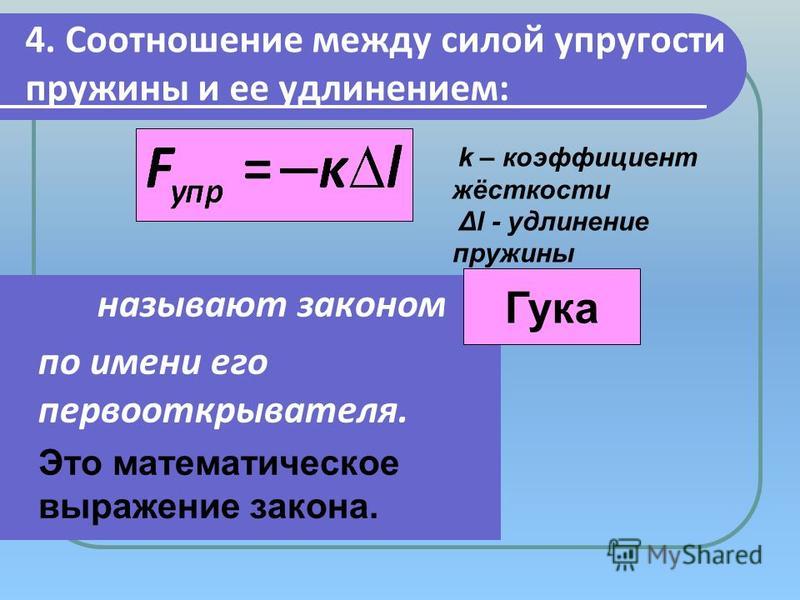

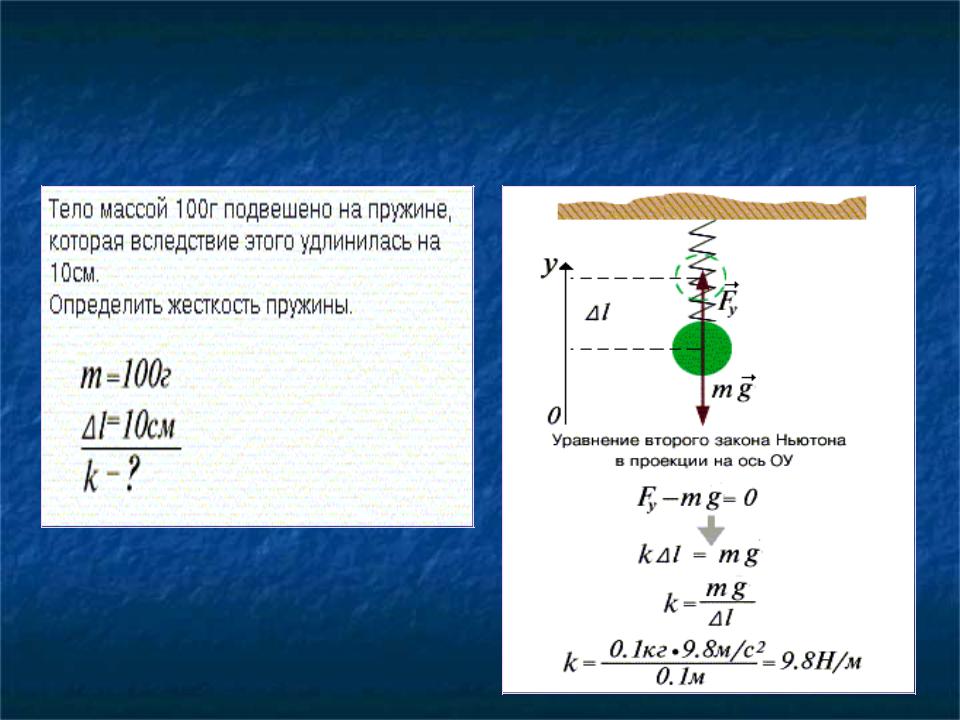
Коэффициент жесткости можно вычислить экспериментально, подвешивая на расположенную вертикально и закрепленную за верхний конец пружину грузы с известной массой. В этом случае имеет место зависимость

$m \cdot g — k \cdot x = 0$,

где $m$ — масса, $g$ — ускорение свободного падения. Отсюда

$k = \frac{m \cdot g}{x}$

Расчет жесткости цилиндрической пружины

Довольно просто понять как работает плоская пружина. Если положить на край письменного стола линейку и прижать один ее конец рукой к поверхности, но второй можно упруго изгибать, запасая и высвобождая энергию. Очевидно, что в момент изгиба расстояния между молекулами материала в некоторых фрагментах линейки увеличиваются, в некоторых уменьшаются. Электромагнитные связи, действующие между молекулами, стремятся вернуть вещество к прежнему геометрическому состоянию.

Несколько сложнее дело обстоит с цилиндрической пружиной. В ней энергия запасается не благодаря деформации изгиба, а за счет скручивания проволоки, из которой пружина навита, относительно продольной оси этой проволоки.

Представим сильно увеличенное сечение проволоки, из которой навита цилиндрическая пружина, выполненное перпендикулярной ее оси плоскостью. При таком рассмотрении можно абстрагироваться от спиральной формы и мысленно разбить весь объем проволоки на множество соприкасающихся торцевыми поверхностями «цилиндров», диаметр которых равен диаметру проволоки, а высота стремится к нулю. Между соприкасающимися торцами действуют молекулярные силы, препятствующие деформации.

При растяжении или сжатии пружины угол наклона между витками изменяется. Соседние «цилиндры» при этом вращаются друг относительно друга в противоположных направлениях вокруг общей оси. В каждом таком сечении запасается энергия. Отсюда следует, что чем из более длинного куска проволоки навита пружина (здесь играют роль диаметр и высота цилиндра, а также шаг витка), тем большее количество энергии она способна запасти. Увеличение диаметра проволоки также повышает ее энергоемкость. В целом формула, учитывающая основные факторы жесткости пружины, выглядит так:

$k = \frac{r^4}{4R^3} \cdot \frac{G}{n}$,

где:

$R$ — радиус цилиндра пружины,
$n$ — количество витков проволоки радиуса $r$,
$G$ — коэффициент, зависящий от материала. {-6}} = 100$
Ответ: $100 \frac{Н}{м}$
Жесткость пружины. Как рассчитать.
Измерение параметров жесткости пружин разных типов
При производстве на предприятии и для применения необходимо определить способность пружины выдерживать определенные типы нагрузок. Для этого высчитывается т.н. коэффициент Гука – обозначение жесткости пружины, от которого зависит её надёжность. На этот параметр влияет материал, выбранный для изготовления. Это может быть сталь, легированная кремнием, ванадием, марганцем, другими добавками. Также применяются нержавейка, бериллиевая и кремнемарганцевая бронза, сплавы на основе никеля и титана.
Если деталь выпускается для применения при высоких нагрузках, экстремальных температурах, используются специальные марки легированной стали. Нижегородская метизная корпорация имеет возможность производить пружины под заказ, создавая изделия с заданными характеристиками.
Что такое жесткость?
Говоря о практике, а не физических терминах, это сила, приложив которую, можно сжать пружину. Если вы знаете прилагаемое усилие, можно определить, какой будет деформация, и наоборот. Это существенно облегчает вычисления.
Коэффициент высчитывается для пружин кручения, растяжения, изгиба, сжатия – всех наиболее популярных в промышленности разновидностей этого изделия. Также следует отметить два основных типа:
- С линейной (постоянной) жесткостью;
- С прогрессивной (зависящей от положения витков) жесткостью.
Часто производитель наносит на готовую продукцию пометку краской. Если такого обозначения нет, применяется формула определения жесткости пружины через массу и длину, упрощающая задачу. Она изначально разрабатывалась для пружин растяжения, была получена методом измерения соответствия массы грузы с изменениями геометрии.
Также данный параметр может быть прогрессирующим – растущим — или регрессирующим – убывающим. Во втором случае параметр «жесткости» принято называть «мягкостью». В отдельных механизмах, например, в автомобилестроении, этот параметр особенно актуален. 3.
Переменная G означает модуль сдвига. Это значение можно найти в таблицах для разных материалов. К примеру, у пружинной стали G=78,5 ГПа.
Далее разберемся, как определить жесткость пружины по формуле:
k=F/L.
Длина L бывает двух типов:
- L1 – измеренная в вертикальном положении без груза;
- L2 – полученная при подвешивании груза с точно известной массой.
Например, 100-граммовая гиря, закреплённая в нижней части, воздействует с силой F, равной 1 Н. Получаем разницу между двумя показателями длины:
L = L2 – L1.
При этом следует уточнить, что степень жесткости не определяет распрямление в исходное состояние. На него воздействуют сразу несколько факторов.
Насколько важен показатель, и на что он влияет?
Характеристики пружины важны не только для соответствия ГОСТам и проведения сертификации. Они влияют на сроки эксплуатации изделий, в которых используются, а это огромное количество приборов, деталей, механизмов, от мебели, до различных транспортных средств.
Поэтому данная величина напрямую влияет на надёжность готовых изделий, оборудования, техники, в которых используются элементы, содержащие пружины.
Часто люди интересуются, как рассчитать жесткость пружины цилиндрической винтовой. Для таких случаев учитывается не только модуль сдвига, но и параметр Rs – напряжение, допускаемое при кручении. Здесь в расчёт берётся тип материала, его физические свойства, механические характеристики.
Следующий вопрос – в чем измеряется коэффициент жесткости пружины при расчётах. Традиционно в системе измерений, принятой в нашей стране принято записывать значение в Н/м – ньютонах на один метр. Также это значение в качестве альтернативного варианта может записываться в килограммах на квадратный сантиметр, дин/см, граммах на квадратный сантиметр (расчёты в системе СГС).
Жесткость пружины. Как рассчитать.
Измерение параметров жесткости пружин разных типов
При производстве на предприятии и для применения необходимо определить способность пружины выдерживать определенные типы нагрузок. Для этого высчитывается т.н. коэффициент Гука – обозначение жесткости пружины, от которого зависит её надёжность. На этот параметр влияет материал, выбранный для изготовления. Это может быть сталь, легированная кремнием, ванадием, марганцем, другими добавками. Также применяются нержавейка, бериллиевая и кремнемарганцевая бронза, сплавы на основе никеля и титана.
Если деталь выпускается для применения при высоких нагрузках, экстремальных температурах, используются специальные марки легированной стали. Нижегородская метизная корпорация имеет возможность производить пружины под заказ, создавая изделия с заданными характеристиками.
Что такое жесткость?
Говоря о практике, а не физических терминах, это сила, приложив которую, можно сжать пружину. Если вы знаете прилагаемое усилие, можно определить, какой будет деформация, и наоборот. Это существенно облегчает вычисления.
Коэффициент высчитывается для пружин кручения, растяжения, изгиба, сжатия – всех наиболее популярных в промышленности разновидностей этого изделия. Также следует отметить два основных типа:
- С линейной (постоянной) жесткостью;
- С прогрессивной (зависящей от положения витков) жесткостью.
Часто производитель наносит на готовую продукцию пометку краской. Если такого обозначения нет, применяется формула определения жесткости пружины через массу и длину, упрощающая задачу. Она изначально разрабатывалась для пружин растяжения, была получена методом измерения соответствия массы грузы с изменениями геометрии.
Также данный параметр может быть прогрессирующим – растущим — или регрессирующим – убывающим. Во втором случае параметр «жесткости» принято называть «мягкостью». В отдельных механизмах, например, в автомобилестроении, этот параметр особенно актуален.
Какие вводные данные требуются?
При расчёте важно знать следующую информацию:
- Из какого материала выполнено изделие;
- Точный диаметр витков – Dw;
- Общий диаметр самой пружины – Dm;
- Количество витков – Na. 3.
  Переменная G означает модуль сдвига. Это значение можно найти в таблицах для разных материалов. К примеру, у пружинной стали G=78,5 ГПа.
  Далее разберемся, как определить жесткость пружины по формуле:
  k=F/L.
  Длина L бывает двух типов:
  - L1 – измеренная в вертикальном положении без груза;
  - L2 – полученная при подвешивании груза с точно известной массой.
  Например, 100-граммовая гиря, закреплённая в нижней части, воздействует с силой F, равной 1 Н. Получаем разницу между двумя показателями длины:
  L = L2 – L1.
  При этом следует уточнить, что степень жесткости не определяет распрямление в исходное состояние. На него воздействуют сразу несколько факторов.
  Насколько важен показатель, и на что он влияет?
  Характеристики пружины важны не только для соответствия ГОСТам и проведения сертификации. Они влияют на сроки эксплуатации изделий, в которых используются, а это огромное количество приборов, деталей, механизмов, от мебели, до различных транспортных средств.
  Поэтому данная величина напрямую влияет на надёжность готовых изделий, оборудования, техники, в которых используются элементы, содержащие пружины.
  Часто люди интересуются, как рассчитать жесткость пружины цилиндрической винтовой. Для таких случаев учитывается не только модуль сдвига, но и параметр Rs – напряжение, допускаемое при кручении. Здесь в расчёт берётся тип материала, его физические свойства, механические характеристики.
  Следующий вопрос – в чем измеряется коэффициент жесткости пружины при расчётах. Традиционно в системе измерений, принятой в нашей стране принято записывать значение в Н/м – ньютонах на один метр. Также это значение в качестве альтернативного варианта может записываться в килограммах на квадратный сантиметр, дин/см, граммах на квадратный сантиметр (расчёты в системе СГС).
  Пружины по цветам — цветовая маркировка жесткости пружин амортизаторов
  Пружины подвески автомобиля отличаются функциональностью. Для повышения комфортности дальних поездок, а равно и благоприятного влияния на управление транспортным средством важно грамотно выбрать пружины. Правильная работа этих элементов снизит уровень износа кузова и главных узлов. Пружины обязательно маркируются в строгой зависимости от цвета и жесткости.
  Виды пружин
  Существует четыре основных вида пружин:
  - Стандартные. Это базовый вариант, его устанавливают на заводах. Такие пружины предназначены для работы в стандартных условиях.
  - Усиленные. Подходят для бездорожья, при частых перевозках крупных грузов.
  - Завышающие. Увеличивают грузоподъёмность.
  - Занимающие. Подходят для ценителей спортивной езды.
  Такие пружины способны сместить центр тяжести транспортного средства к нижней части.
  Маркировка и классификация
  Маркировка по цветам способна разрешить проблему выбора для автолюбителей, но одновременно является результатом сложного процесса. Каждый этап проконтролировать сложно. По этой причине проводят анализ готовой продукции. Так и появился способ классификации по цвету. Таким образом, можно отличить элементы между собой. Есть и иные варианты, но данный способ отличается простотой и надёжностью.
  Различаются пружины и по параметру. Его определяет разработчик автомобиля, при производстве изменить его нельзя. Но от производителя зависит:
  - диаметр пружинного прута;
  - степень жёсткости.
  Эти элементы различаются по цвету, другим способом степень жёсткости не определить. Они окрашены в разнообразную цветовую палитру, но параметр жёсткости определить не составит труда.
  Для автомобилей ВАЗ подходят два класса, они окрашены в следующие цвета:
  - Класс А маркируют белым, жёлтым, оранжевым или коричневым.
  - Класс В – чёрным, синим, голубым и жёлтым.
  Чтобы выяснить, какая жёсткость у определённой пружины, следует посмотреть на полоску, она находится на наружной стороне витка. При этом окраска может быть другой. Цвет пружины зависит от защитного покрытия. Оно сбережёт от разрушения. Обычно применяют эпоксидную или хлоркаучуковую эмаль. Разобраться в маркировке пружин можно исключительно по цвету полоски на витках.
  Цвет поверхности находится в зависимости от модели автомобиля, а равно и места, куда пружину устанавливают – в переднюю либо заднюю часть. Передние элементы покрывают в чёрный цвет.
  Использование и отличия
  Пружины различаются по цветам с целью помочь водителю правильно подобрать их для замены. На автомобиль разрешено устанавливать пружины и класса А и В, но цвета должны быть идентичными. Если это правило нарушить, кузов будет крениться на одну сторону. Крен приведёт к худшей управляемости и устойчивости транспортного средства. Различный цвет пружин будет причиной быстрого износа ходовой части.
  Нельзя устанавливать на машину пружины разных классов. При этом на переднюю ось можно поставить пружины класса А, на заднюю – класса В. Другой порядок недопустим. Цвет и класс должны быть одинаковыми.
  Считается, что пружины класса А жёстче, чем элементы класса В, причём независимо от цвета. Это верно только отчасти. Класс «А» идеален для транспортных средств с большей нагрузкой. Следует отметить, что встречаются образцы пружин без обязательной маркировки. Такие элементы не стоит приобретать и тем более использовать.
  Устанавливать следует исключительно пружины надлежащего качества, они обеспечат мягкую езду, небольшой износ транспортного средства и среднюю нагрузку на автолюбителя.
  Коэффициент жесткости пружины: определение, формулы, измерение
  Пружины можно назвать одной из наиболее распространенных деталей, которые являются частью простых и сложных механизмов. При ее изготовлении применяется специальная проволока, накручиваемая по определенной траектории. Выделяют довольно большое количество различных параметров, характеризующих это изделие. Наиболее важным можно назвать коэффициент жесткости. Он определяет основные свойства детали, может рассчитываться и применяться в других расчетах. Рассмотрим особенности подобного параметра подробнее.
  Определение и формула жесткости пружины
  При рассмотрении того, что такое коэффициент жесткости пружины следует уделить внимание понятию упругости. Для ее обозначения применяется символ F. При этом сила упругости пружины характеризуется следующими особенностями:
  1. Проявляется исключительно при деформации тела и исчезает в случае, если деформация пропадает.
  2. При рассмотрении, что такое жесткость пружины следует учитывать, после снятия внешней нагрузки тело может восстанавливать свои размеры и форму, частично или полностью. В подобном случае деформация считается упругой.
  Не стоит забывать о том, что жесткость – характеристика, свойственная упругим телам, способным деформироваться. Довольно распространенным вопросом можно назвать то, как обозначается жесткость пружины на чертежах или в технической документации. Чаще всего для этого применяется буква k.
  Слишком сильная деформация тела становится причиной появления различных дефектов. Ключевыми особенностями можно назвать следующее:
  1. Деталь может сохранять свои геометрические параметры при длительной эксплуатации.
  3. При увеличении показателя существенно снижается сжатие пружины под воздействие одинаковой силы.
  4. Наиболее важным параметром можно назвать коэффициент жесткости. Он зависит от геометрических показателей изделия, типа применяемого материала при изготовлении.
  Довольно большое распространение получили красные пружины и другого типа. Цветовое обозначение применяется в случае производства автомобильных изделий. Для расчета применяется следующая формула: k=Gd⁴/8D³n. В этой формуле указываются нижеприведенные обозначения:
  1. G – применяется для определения модуля сдвига. Стоит учитывать, что это свойство во многом зависит от применяемого материала при изготовлении витков.
  2. d – диаметральный показатель проволоки. Она производится путем проката. Этот параметр указывается также в технической документации.
  3. D – диаметр создаваемых витков при накручивании проволоки вокруг оси. Он подбирается в зависимости от поставленных задач. Во многом диаметр определяет то, какая нагрузка оказывается для сжатия устройства.
  4. n – число витков. Этот показатель может варьировать в достаточно большом диапазоне, также влияет на основные эксплуатационные характеристики изделия.
  Рассматриваемая формула применяется в случае расчета коэффициента жесткости для цилиндрических пружин, которые устанавливаются в самых различных механизмах. Подобная единица измеряется в Ньютонах. Коэффициент жесткости для стандартизированных изделий можно встретить в технической литературе.
  Формула жесткости соединений пружин
  Не стоит забывать о том, что в некоторых случаях проводится соединение тела нескольким пружинами. Подобные системы получили весьма широкое распространение. Определить жесткость в этом случае намного сложнее. Среди особенностей соединения можно отметить нижеприведенные моменты:
  1. Параллельное соединение характеризуется тем, что детали размещаются последовательно. Подобный метод позволяет существенно повысить упругость создаваемой системы.
  2. Последовательный метод характеризуется тем, что деталь подключаются друг к другу. Подобный способ подсоединения существенно снижает степень упругости, однако позволяет существенно увеличить максимальное удлинение. В некоторых случаях требуется именно максимальное удлинение.
  В обеих случаях применяется определенная формула, которая определяет особенности подключения. Модуль силы упругости может существенно отличаться в зависимости от особенностей конкретного изделия.
  При последовательном соединении изделий показатель рассчитывается следующим образом: 1/k=1/k₁+1/k₂+…+1/k_n. Рассматриваемый показатель считается довольно важным свойством, в данном случае он снижается. Параллельный метод подключения рассчитывается следующим образом: k=k₁+k₂+…k_n.
  Подобные формулы могут использоваться при самых различных расчетах, чаще всего на момент решения математических задач.
  Коэффициент жесткости соединений пружин
  Приведенный выше показатель коэффициента жесткости детали при параллельном или последовательном соединении определяет многие характеристики соединения. Довольно часто проводится определение тому, чему равно удлинение пружины. Среди особенностей параллельного или последовательного соединения можно отметить нижеприведенные моменты:
  1. При параллельном подключении удлинение обоих изделий будет равным. Не стоит забывать о том, что оба варианта должны характеризоваться одинаковой длиной в свободном положении. При последовательном показатель увеличивается в два раза.
  2. Свободное положение – ситуация, в которой деталь находится без прикладывания нагрузки. Именно оно в большинстве случаев учитывается при проведении расчетов.
  3. Коэффициент жесткости изменяется в зависимости от применяемого способа подсоединения. В случае параллельного соединения показатель увеличивается в два раза, при последовательном уменьшается.
  Для проведения расчетов нужно построить схему подключения всех элементов. Основание представлено линией со штриховкой, изделие обозначается схематически, а тело в упрощенном виде. Кроме этого, от упругой деформации во многом зависит кинетическая и другая энергия.
  Коэффициент жесткости цилиндрической пружины
  На практике и в физике довольно большое распространение получили именно цилиндрические пружины. Их ключевыми особенностями можно назвать следующие моменты:
  1. При создании указывается центральная ось, вдоль которой и действует большинство различных сил.
  2. При производстве рассматриваемого изделия применяется проволока определенного диаметра. Она изготавливается из специального сплава или обычных металлов. Не стоит забывать о том, что материал должен обладать повышенной упругостью.
  3. Проволока накручивается витками вдоль оси. При этом стоит учитывать, что они могут быть одного или разного диаметра. Довольно большое распространение получил вариант исполнения цилиндрического типа, но большей устойчивостью характеризуется цилиндрический вариант исполнения, в сжатом состоянии деталь обладает небольшой толщиной.
  4. Основными параметрами можно назвать больший, средний и малый диаметр витков, диаметр проволоки, шаг расположения отдельных колец.
  Не стоит забывать о том, что выделяют два типа деталей: сжатия и растяжения. Их коэффициент жесткости определяется по одной и той же формуле. Разница заключается в следующем:
  1. Вариант исполнения, рассчитанный на сжатие, характеризуется дальним расположением витков. За счет расстояние между ними есть возможность сжатия.
  2. Модель, рассчитанная на растяжение, имеет кольца, расположенные практически вплотную. Подобная форма определяет то, что при максимальная сила упругости достигается при минимальном растяжении.
  3. Также есть вариант исполнения, который рассчитан на кручение и изгиб. Подобная деталь рассчитывается по определенным формулам.
  Расчет коэффициента цилиндрической пружины может проводится при использовании ранее указанной формулы. Она определяет то, что показатель зависит от следующих параметров:
  1. Наружного радиуса колец. Как ранее было отмечено, при изготовлении детали применяется ось, вокруг которой проводится накручивание колец. При этом не стоит забывать о том, что выделяют также средний и внутренний диаметр. Подобный показатель указывается в технической документации и на чертежах.
  2. Количества создаваемых витков. Этот параметр во многом определяет длину изделия в свободном состоянии. Кроме этого, количество колец определяет коэффициент жесткость и многие другие параметры.
  3. Радиуса применяемой проволоки. В качестве исходного материала применяется именно проволока, которая изготавливается из различных сплавов. Во многом ее свойства оказывают влияние на качества рассматриваемого изделия.
  4. Модуля сдвига, который зависит от типа применяемого материала.
  Коэффициент жесткости считается одним из наиболее важных параметров, который учитывается при проведении самых различных расчетов.
  Единицы измерения
  При проводимых расчетах также должно учитываться то, в каких единицах измерениях проводятся вычисления. При рассмотрении того, чему равно удлинение пружины уделяется внимание единице измерения в Ньютонах.
  Для того чтобы упростить выбор детали многие производители указывают его цветовым обозначением.
  Разделение пружины по цветам проводится в сфере автомобилестроения.
  Среди особенностей подобной маркировки отметим следующее:
  1. Класс А обозначается белым, желтым, оранжевым и коричневым оттенками.
  2. Класса В представлен синим, голубым, черным и желтым цветом.
  Как правило, подобное свойство отмечается на внешней стороне витка. Производители наносят небольшую полоску, которая и существенно упрощает процесс выбора.
  Особенности расчета жесткости соединений пружин
  Приведенная выше информация указывает на то, что коэффициент жесткости является довольно важным параметром, который должен рассчитываться при выборе наиболее подходящего изделия и во многих других случаях. Именно поэтому довольно распространенным вопросом можно назвать то, как найти жесткость пружины. Среди особенностей соединения отметим следующее:
  1. Провести определение растяжения пружины можно при вычислении, а также на момент теста. Этот показатель может зависеть в зависимости от проволоки и других параметров.
  2. Для расчетов могут применяться самые различные формулы, при этом получаемый результат будет практически без погрешностей.
  3. Есть возможность провести тесты, в ходе которых и выявляются основные параметры. Определить это можно исключительно при применении специального оборудования.
  Как ранее было отмечено, выделяют последовательный и параллельный метод соединения. Оба характеризуются своими определенными особенностями, которые должны учитываться.
  В заключение отметим, что рассматриваемая деталь является важной частью конструкции различных механизмов. Неправильный вариант исполнения не сможет прослужить в течение длительного периода. При этом не стоит забывать о том, что слишком сильная деформация становится причиной ухудшения эксплуатационных характеристик.
  Моделирование показывает, почему у легендарных прыгунов разная «пружинная» жесткость
  Новое исследование может объяснить, почему у лягушек и кузнечиков такие разные «пружины» для прыжков. Предоставлено: Wikimedia Commons: AtelierMonpli, Карл Д. Хоу.
  В новом исследовании рассказывается история кузнечика и лягушки-быка, но это не детская сказка. Вместо этого он описывает биомеханическое моделирование, которое помогает объяснить, почему у двух прыгающих животных очень разная жесткость пружин — сухожилий лягушек и их двойников, называемых аподемами у кузнечиков, — которые хранят энергию для их прыжков.Наука предполагает, что разница в том, сколько времени они обычно проводят до взлета.
  «Наше моделирование согласуется с гипотезой о том, что жесткость пружины варьируется среди организмов в зависимости от их прыжков — независимо от того, ограничены они во времени или не ограничены во времени», — сказал Майкл Розарио, научный сотрудник Университета Брауна и ведущий автор исследование Proceedings of the Royal Society B .
  Ученые уже знали, что основная пружина кузнечика (аподема и часть его экзоскелета) имеет более чем в два раза жесткость, чем аналогичное сухожилие у лягушки-быка. Моделируя систему мышечных пружин в ногах каждого существа, Розарио и его соавторы смогли показать, что чем больше времени у животного для сокращения мышц для накопления энергии перед прыжком, тем больше энергии они могут хранить в относительно жесткой пружине. .
  Кузнечики (Schistocerca gregaria) обычно тратят 300 миллисекунд, накапливая энергию в своих мышцах, аподемах и экзоскелетах, хотя им нужно прыгать быстрее и, возможно, менее эффективно, чтобы уклоняться от хищников.С другой стороны, лягушки-быки (Lithobates catesbeiana) обычно тратят всего 50 миллисекунд перед прыжком, например, чтобы наброситься на добычу. Моделирование показало, что наибольший запас энергии для быстрого прыжка, такого как у лягушки-быка, был в менее жесткой пружине, в то время как для периода времени кузнечика она была в более жесткой пружине.
  Другими словами, существа обладают той пружинящей жесткостью, которую они должны иметь, учитывая временные ограничения их типичного прыжкового поведения.
  «И для лягушки-быка, и для кузнечика время, доступное для сокращения мышц, определяло, какая жесткость пружины обеспечивает максимальное накопление энергии», — писали Розарио и его коллеги из Университета Дьюка (где он провел большую часть исследований, прежде чем завершить их в Брауне), University Бристоля, Государственного университета Северной Каролины и Университета Северной Каролины.
  Росарио и его коллеги утверждают, что эта статья может помочь предсказать свойства мышц и сухожилий для других организмов, включая млекопитающих. Дальнейшие исследования, которые Розарио проводит в лаборатории профессора Университета Брауна Томаса Робертса, определят, не слишком ли это большой скачок.
  Удивительные прыжки лягушек на упругих сухожилиях
  Дополнительная информация: М.V. Rosario et al. Мышечно-пружинная динамика в ограниченных по времени эластичных движениях, Труды Королевского общества B: Биологические науки (2016). DOI: 10.1098 / rspb.2016.1561 Предоставлено Брауновский университет
  Ссылка : Моделирование показывает, почему у легендарных прыгунов разная «пружинная» жесткость (2016, 16 сентября) получено 12 января 2021 г. с https: // физ.org / news / 2016-09-simulator-posits-legendary-leapers-stiffness.html
  Этот документ защищен авторским правом. За исключением честных сделок с целью частного изучения или исследования, никакие часть может быть воспроизведена без письменного разрешения. Контент предоставляется только в информационных целях.
  Пружины растяжения
  : как измерить натяжение
  Что такое начальное натяжение пружины растяжения?
  Начальное натяжение — это натяжная намотка между витками пружины растяжения.Он держит катушки закрытыми и требует внешней силы перед открытием катушек. Чтобы снять начальное напряжение, вы должны растягивать пружину растяжения до тех пор, пока через витки не будет светить.
  В отличие от пружины сжатия, пружина растяжения может иметь предварительную нагрузку при нулевом прогибе. Величина силы, создаваемой пружиной растяжения, является важной частью ее конструкции и производства, поскольку она влияет на характеристики пружины. Узнайте, как измерить начальное натяжение пружины ниже.
  Формула начального натяжения: как измерить натяжение пружины
  Начальное натяжение пружины растяжения можно рассчитать по простой формуле:
  П ₁ = П — П (Т)
  Переменные в этом уравнении представляют следующее:
  - P ₁ = начальное натяжение
  - P = нагрузка
  - R = ставка
  - T = Путешествие
  Например, где R = 10 фунтов на дюйм, P = 20 фунтов и T = 1.5 дюймов, вы можете найти фунты силы для начального натяжения пружины. Просто умножьте 10 на 1,5 и вычтите из 20, чтобы получить 5 фунтов силы (5 фунтов силы).
  П ₁ = 20-10 * 1,5
  P ₁ = 20 — 10
  P ₁ = 5 фунтов
  Чтобы узнать больше об этом уравнении и терминологии растягивающейся пружины, ознакомьтесь с нашим глоссарием терминов по форме пружины и проволоки.
  Если вам нужна помощь в вычислении начального натяжения или в обучении измерению пружины, свяжитесь с нами.В Master Spring мы помогаем OEM-производителям определить лучшую форму пружины или проволоки для их нужд. Чтобы начать работу, запросите бесплатное предложение пружины расширения сегодня и включите следующую информацию:
  - Высота или длина в свободном, установленном и полностью нагруженном положении пружины
  - Размер полости (отверстия), в которое входит пружина
  - Размер стержня или оправки, на которую подходит пружина
  - Описание ответной части
  Получите бесплатное предложение
  Напряжение, напряжение и закон Гука — Урок
  Напряжение, напряжение и закон Гука — Урок — TeachEngineering
  Быстрый просмотр
  Уровень оценки: 11 (10-12)
  Требуемое время: 1 час 15 минут
  Урок Зависимость:
  Тематические области: Физические науки, физика
  Подпишитесь на нашу рассылку новостей
  Резюме
  Студенты знакомятся с законом Гука, а также с отношениями стресс-напряжение.Сначала они изучают основные уравнения, затем работают над несколькими примерами задач, сначала индивидуально, а затем в классе. В ходе занятия, состоящего из двух частей, учащиеся: 1) исследуют закон Гука путем экспериментального определения неизвестной жесткости пружины, а затем 2) применяют полученные знания для создания графика деформации, изображающего опухоль, с помощью Microsoft Excel®. После занятий урок завершается тестом на стресс-напряжение, чтобы оценить понимание понятий каждым учащимся.
  Инженерное соединение
  Более 300 лет назад Роберт Гук определил пропорциональность, которая до сих пор остается фундаментальной концепцией для физиков и инженеров.Хотя его «закон» был установлен только для пружин, с тех пор он применяется ко всем материалам с известной площадью поверхности. Взаимосвязь, которую сегодня чаще всего используют, — это прямая пропорциональность между напряжением и напряжением. Вместе инженеры-строители, инженеры-механики и специалисты по материалам тщательно выбирают конструкционные материалы, которые способны безопасно выдерживать повседневные нагрузки, оставаясь при этом в упругой области кривой зависимости напряжения от деформации, в противном случае возникает необратимая деформация. Архитекторы, которые когда-то выбирали камень из-за его эстетической привлекательности, теперь выбирают сталь из-за ее долговечности.Для биомедицинских инженеров титан часто является материалом выбора из-за его биосовместимости и, что более важно, его способности выдерживать растягивающее и сжимающее напряжение веса тела. В предоставленном наборе задач учащиеся изучают приложения закона Гука и отношения напряжения и деформации. В частности, в задаче 7 студенты применяют эти отношения к тканям тела, как это сделали бы биомедицинские инженеры.
  Цели обучения
  После этого урока учащиеся должны уметь:
  - Объясните концепции напряжения и деформации и взаимосвязь между ними.
  - Объясните закон Гука и примените его для анализа пружин.
  - Используйте Microsoft Excel®, чтобы построить простой график деформации.
  - Соотнесите напряжение и деформацию с инженерной задачей устройства.
  Образовательные стандарты Каждый урок или задание TeachEngineering соотносится с одним или несколькими научными предметами K-12, образовательные стандарты технологии, инженерии или математики (STEM).
  Все 100000+ стандартов K-12 STEM, охватываемых TeachEngineering , собираются, обслуживаются и упаковываются Сетью стандартов достижений (ASN) , проект Д2Л (www.achievementstandards.org).
  В ASN стандарты имеют иерархическую структуру: сначала по источникам; например , по штатам; внутри источника по типу; например , естественные науки или математика; внутри типа по подтипу, затем по классу, и т. д. .
  
  Общие основные государственные стандарты — математика
  - Докажите, что для данной системы двух уравнений с двумя переменными замена одного уравнения суммой этого уравнения и кратным другому дает систему с такими же решениями.(Оценки 9 — 12) Подробнее
    Посмотреть согласованную учебную программу
    Вы согласны с таким раскладом? Спасибо за ваш отзыв!
  - Используйте единицы как способ понять проблемы и направить решение многоэтапных проблем; последовательно выбирать и интерпретировать единицы в формулах; выберите и интерпретируйте масштаб и начало координат на графиках и дисплеях данных.(Оценки 9 — 12) Подробнее
    Посмотреть согласованную учебную программу
    Вы согласны с таким раскладом? Спасибо за ваш отзыв!
  - Обобщение, представление и интерпретация данных по одному счету или измеряемой переменной (Оценки 9 — 12) Подробнее
    Посмотреть согласованную учебную программу
    Вы согласны с таким раскладом? Спасибо за ваш отзыв!
  - Обобщение, представление и интерпретация данных по двум категориальным и количественным переменным. (Оценки 9 — 12) Подробнее
    Посмотреть согласованную учебную программу
    Вы согласны с таким раскладом? Спасибо за ваш отзыв!
  Международная ассоциация преподавателей технологий и инженерии — Технология
  - Телемедицина отражает конвергенцию технологических достижений в ряде областей, включая медицину, телекоммуникации, виртуальное присутствие, компьютерную инженерию, информатику, искусственный интеллект, робототехнику, материаловедение и психологию восприятия.(Оценки 9 — 12) Подробнее
    Посмотреть согласованную учебную программу
    Вы согласны с таким раскладом? Спасибо за ваш отзыв!
  - Определите критерии и ограничения и определите, как они повлияют на процесс проектирования.(Оценки 9 — 12) Подробнее
    Посмотреть согласованную учебную программу
    Вы согласны с таким раскладом? Спасибо за ваш отзыв!
  - Используйте компьютеры и калькуляторы для доступа, извлечения, организации, обработки, обслуживания, интерпретации и оценки данных и информации в целях общения.(Оценки 9 — 12) Подробнее
    Посмотреть согласованную учебную программу
    Вы согласны с таким раскладом? Спасибо за ваш отзыв!
  ГОСТ
  Мэриленд — наука
  Теннесси — Математика
  - Используйте единицы как способ понять проблемы и направить решение многоэтапных проблем; последовательно выбирать и интерпретировать единицы в формулах; выберите и интерпретируйте масштаб и начало координат на графиках и дисплеях данных.(Оценки 9 — 12) Подробнее
    Посмотреть согласованную учебную программу
    Вы согласны с таким раскладом? Спасибо за ваш отзыв!
  - Обобщение, представление и интерпретация данных по одному счету или измеряемой переменной (Оценки 9 — 12) Подробнее
    Посмотреть согласованную учебную программу
    Вы согласны с таким раскладом? Спасибо за ваш отзыв!
  - Обобщение, представление и интерпретация данных по двум категориальным и количественным переменным. (Оценки 9 — 12) Подробнее
    Посмотреть согласованную учебную программу
    Вы согласны с таким раскладом? Спасибо за ваш отзыв!
  - Докажите, что для данной системы двух уравнений с двумя переменными замена одного уравнения суммой этого уравнения и кратным другому дает систему с такими же решениями.(Оценки 9 — 12) Подробнее
    Посмотреть согласованную учебную программу
    Вы согласны с таким раскладом? Спасибо за ваш отзыв!
  Теннесси — Наука
  Предложите выравнивание, не указанное выше
  Какое альтернативное выравнивание вы предлагаете для этого контента?
  Рабочие листы и приложения
  Посетите [www.teachengineering.org/lessons/view/van_cancer_lesson2], чтобы распечатать или загрузить.
  Больше подобной программы
  Механика упругого твердого тела
  Учащиеся вычисляют напряжение, деформацию и модуль упругости, а также узнают о типичной инженерной диаграмме напряжения-деформации (графике) упругого материала.
  Эластичность и модуль Юнга для анализа тканей
  В рамках процесса инженерного проектирования для создания тестируемых моделей сердечных клапанов учащиеся узнают о силах, действующих в человеческом теле, чтобы открывать и закрывать аортальные клапаны.Они узнают о силах кровотока, эластичности, напряжении, деформации, структуре клапана и свойствах тканей, а также о модуле Юнга, включая …
  Применение закона Гука для обнаружения рака
  Студенты изучают закон Гука, работая в небольших группах на своих лабораторных скамьях.Они собирают данные о смещении пружин с неизвестной константой пружины k путем добавления различных масс известного веса.
  Напряженная и деформированная
  Студенты знакомятся с понятиями стресса и напряжения с примерами, которые иллюстрируют характеристики и важность этих сил в нашей повседневной жизни.Они исследуют факторы, влияющие на стресс, почему инженерам нужно знать о нем и как инженеры описывают силу материи …
  Предварительные знания
  Базовое понимание алгебры и способность решать простые алгебраические выражения.Кроме того, понимание проблемы обнаружения рака, представленной на предыдущем уроке.
  Введение / Мотивация
  В сегодняшнем уроке мы начнем узнавать о законе Гука, а затем узнаем, как применить эту пропорциональность к тканям тела. Мы точно узнаем, что описывают термины «напряжение» и «деформация», а также их взаимосвязь. Изучив материал урока, я раздам раздаточный материал с примерами задач.Сначала проработайте их в меру своих возможностей независимо; затем мы рассмотрим проблемы всем классом.
  После знакомства с новыми уравнениями мы исследуем закон Гука в соответствующей деятельности (Применение закона Гука для обнаружения рака) путем экспериментального определения неизвестной константы пропорциональности. После изучения закона Гука, во второй части упражнения мы начнем применять полученные знания для разработки средств визуализации тканей тела, и вскоре мы сможем обнаруживать злокачественные опухоли!
  Вы также попрактикуетесь в графическом отображении подготовленных данных для изображения раковой ткани.После того, как мы усвоим этот материал, у нас будет тест на стресс, деформацию и закон Гука. Пожалуйста, делайте подробные записи и обязательно задавайте любые вопросы о примерах проблем, над которыми мы будем работать.
  Возвращаясь к унаследованному циклу, который мы обсуждали в предыдущем уроке, сегодняшний урок представляет собой фазу исследования и пересмотра. Вернитесь к своим первоначальным мыслям и запишите любую новую информацию, которая применима к решению проблемы. Ваша цель сегодня — пересмотреть, пересмотреть и расширить свои текущие знания! Теперь давайте узнаем, как обнаружить рак.
  Предпосылки и концепции урока для учителей
  Устаревшая информация цикла
  Этот урок попадает в фазу «Исследование и пересмотр » старого цикла. Студенты начинают изучать основные концепции, необходимые для создания графика деформации для изображения раковой ткани. После этого урока попросите учащихся пересмотреть свои первоначальные мысли, а по завершении соответствующего задания учащиеся должны иметь навыки, необходимые для того, чтобы Go Public предлагал решение.Но перед тем, как Going Public , попросите учащихся пройти тест на стресс, напряжение и закон Гука в рамках фазы Test Your Mettle старого цикла. Викторина служит формирующим оцениванием, в то время как этап Go Public следующего урока представляет собой итоговую оценку.
  Информация о лекции
  В конце 1600-х годов Роберт Гук заявил, что «сила любого упругого тела находится в той же пропорции, что и расширение». Хотя закон Гука остался в силе и сегодня, его формулировка была исправлена, заменив власть силой.Этот закон объясняется прямой пропорциональностью между сжатием или расширением пружины и возникающей восстанавливающей силой. Соотношение задается следующим образом: F = -k * Δx , где Δx — расстояние, на которое была растянута пружина, F — возвращающая сила, прикладываемая пружиной, а k — жесткость пружины, которая характеризует упругие свойства материал пружины. Этот закон действует в пределах упругости линейной пружины, когда она действует по поверхности без трения.
  Продолжая исследование пружин, Гук становится очевидным, что большинство материалов действуют как пружины с силой, прямо пропорциональной смещению. Но по сравнению с пружинами другие материалы обладают площадью, которую необходимо учитывать. Заменяя силу мерой напряжения и смещения мерой деформации, можно получить следующее выражение: σ = E * ε . Теперь мы исследуем меры стресса и деформации.
  Напряжение — это мера средней силы на единицу площади, определяемая по формуле σ = F / A , где среднее напряжение σ равно силе F , действующей по площади, A .