Матричная оптика – Как устроена матричная оптика: — Журнал Движок.

Как устроена матричная оптика: — Журнал Движок.

Постепенный переход на светодиодные источники света в автомобилях уже несомненная тенденция. Лампы накаливания в ближайшем будущем останутся уделом устаревших конструкций. А сейчас высокоэффективные и долговечные фары постепенно отвоевывают позиции у традиционных. В маломощных осветительных приборах светодиоды уже вытеснили конкурентов, а вот в области головного света сражение еще идет. И основное оружие светодиодов — матричная оптика конструкции Hella.

 

Просто заменить газоразрядный или галогенный источник света на светодиоды — идея не новая. Еще в 2008 году подобная система появилась на машинах Lexus LS, а сейчас построенная по тому же принципу головная оптика стала базовой на многих массовых автомобилях. Например, новый кроссовер Skoda Kodiaq оснащен ею в базовой комплектации, как и соплатформенный VW Tiguan. На базе подобной конструкции можно создать даже адаптивное освещение, и оно не будет ничем принципиально отличаться от использующего газоразрядные источники света. Но настоящий прорыв в эффективности дает только матричная светодиодная оптика.

Качественный головной свет автомобиля должен быть не только ярким, но и освещать исключительно необходимые зоны. Кроме того, не слепить встречных водителей, выделять важные объекты и при этом учитывать особенности человеческого глаза в отношении контрастности освещения и светотеневой границы.

Адаптивное головное освещение на базе единого источника света во многом решает эти сложности, но настоящий прорыв возможен только при использовании матричного освещения, когда за каждую зону отвечает отдельный источник света с регулируемой яркостью, а управляется система интеллектуальным модулем, способным распознавать объекты перед машиной и регулировать освещенность различных зон по ситуации. И именно по этому пути пошла компания Hella при разработке своих матричных светодиодных модулей адаптивного освещения.

Идея использовать много фар для освещения нескольких зон перед машиной в случае традиционных источников света сталкивается с габаритными ограничениями. И газоразрядные источники света, и лампы накаливания имеют достаточно крупные размеры рабочей области и требуют объемной оптической системы.

В случае со светодиодным освещением такая проблема не стоит. Если отказаться от использования сменных светодиодных модулей, то на небольшой плате можно разместить более 50 светодиодов, а поскольку их световой поток имеет явную направленность, то подобная матрица диодов отлично работает с компактной и простой оптической системой.

На практике в оптике Audi Matrix LED с 25 светодиодами адаптивного освещения они собраны в сменные модули по пять светодиодов в каждом, и еще пять модулей используются для статического освещения — ближнего света и статического бокового. В следующем поколении оптических систем Hella, которые с 2016 года устанавливаются на машины Mercedes, применяется целых 84 светодиода на единой плате.

Перспективная LED-оптика разработки Hella по-прежнему имеет «всего» 25 светодиодов на единой плате, но за счет использования в оптической системе фары проекционного LCD-дисплея с разрешением 30 тыс. пикселей с матрицей 100х300 число контролируемых зон освещения возрастает на порядок.

Сложность подобной конструкции легко недооценить. При тех же габаритах, что и у традиционной фары, внутри матричная LED-оптика и ее система управления устроены на порядок сложнее. Чтобы не быть голословным, рассмотрим конструкцию и ее возможности на примере оптики Audi Matrix LED для модели A8 в кузове D4 2013 года. Не самой новой, но зато одной из самых распространенных в России и имеющей много общего со светодиодной матричной оптикой других машин Audi. На следующих поколениях и для других моделей, скорее всего, будет уже лазерный источник света.

Возможности и конструкция

Помимо конструкции самой оптической системы, важную роль для работы адаптивного освещения играет конструкция системы управления. В случае с матричной оптикой самым важным датчиком системы является LiDAR — дальномер оптического диапазона, позволяющий системе управления получить предоставления обо всех источниках света и объектах в зоне освещения головной оптики. Так же используются данные навигационной системы, датчики скорости автомобиля, дождя и освещенности и данные ассистента ночного видения, если он есть в автомобиле. На основании этих данных блок управления может использовать один из множества режимов работы.

Дальний свет для движения по автомагистрали включается на основании данных навигационной системы. В этом случае система Matrix Beam включает узкий луч с максимальной дальностью освещения, наилучшим образом подходящий для ночных поездок на высокой скорости.

Ближний свет с классической асимметричной формой светового пучка использует 15 отдельных светодиодов в каждой фаре и включается в населенных пунктах. Может применяться отдельно от адаптивного освещения. Дальняя зона освещения реализуется отдельным набором светодиодов и может быть отключена для реализации туристического или всепогодного режима.

Туристический режим используется при движении в странах с левосторонним движением для машин, созданных для движения правостороннего. Он позволяет уменьшить асимметрию светового луча при включенном режиме ближнего света. Включается режим или автоматически, по данным навигационной системы, или вручную, через меню мультимедийной системы.

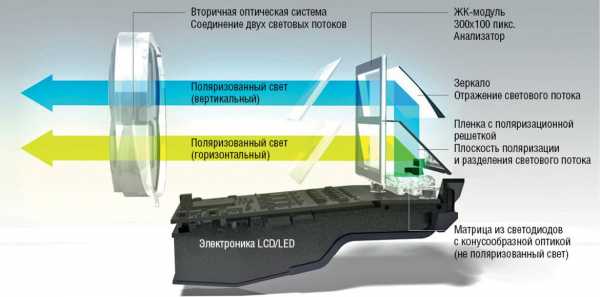
Конструкцию основной оптической системы фары можно увидеть на рисунке, но помимо нее в конструкцию входят также модуль указателя поворота (разумеется, со светодиодами), модуль охлаждения, причем со сменным вентилятором, и внутренняя проводка.

Статическое освещение боковой зоны предназначено для облегчения маневрирования и безопасного проезда перекрестков. Специальная секция фары освещает широкую зону спереди-сбоку от автомобиля. Включается автоматически при малой скорости и включении указателя поворотов, а также при угле поворота рулевого колеса более 50 градусов и скорости менее 60 км/ч. При проезде перекрестков срабатывает режим освещения для перекрестков, который включается по данным навигационной системы и скорости менее 60 км/ч.

Всепогодное освещение используется в условиях тумана и снегопада. В этом случае снижается мощность ближнего света и включается статическое освещение боковых зон. Включается режим вручную, кнопкой на панели, а ассистент дальнего света при этом отключается.

Динамическое адаптивное освещение работает на скорости более 60 км/ч вне населенных пунктов. Используется матрица из 25 светодиодов дальнего света, создающая 25 независимых сегментов. Система обеспечивает изменение направления луча света в зависимости от рельефа, не ослепляет встречный и попутный транспорт, снижает яркость в зонах расположения источников с высоким коэффициентом отражения — дорожных знаков и все другие функции адаптивности.

Маркирующая подсветка пешеходов срабатывает вне населенных пунктов и скорости более 60 км/ч, при наличии ассистента ночного видения. Секции дальнего света фар в направлении пешехода мигают, привлекая внимание водителя, а силуэт пешехода подсвечивается красным на дисплее приборной панели.

Помимо датчика LiDAR в работе системы задействованы блок управления корректора фар и блок комфорта бортовой сети. Причем самих корректоров у адаптивной оптики нет по двум причинам. На машинах с матричной LED-оптикой установлена пневмоподвеска и сама оптика имеет высокий запас адаптивности даже в режиме ближнего света за счет разделения зон. Так что блок управления в строгом смысле слова блоком коррекции уровня не является, просто располагается и подключен так же, как блок коррекции на машинах без этой системы. Помимо внешних блоков, используются три блока контроля в самой фаре.

Конструкция модуля охлаждения для светодиодной оптики крайне важна, так как от него зависит долговечность самих светодиодов и он включает в себя индивидуальные воздуховоды для каждой диодной сборки и множество датчиков. Вместо линз в этом поколении оптики используются зеркальные отражатели, имеющие повышенную стойкость к перегреву. Снаружи корпус закрыт общим герметичным колпаком.

В целом развитие автомобильного света уже семимильными шагами идет по пути внедрения интеллектуального светодиодного освещения, в чем корреспонденты журнала «Движок» убедились на практике, сравнив его с адаптивным биксеноновым. Ну а постепенное удешевление конструкции и ее повсеместное внедрение в ближайшем будущем позволит значительно улучшить ситуацию с освещением на дороге, а следовательно, и с безопасностью.

dvizhok.su

Матричная оптика — Викиучебник

Матричная оптика

Матричная оптика (в дальнейшем МО) представляет собой раздел вычислительной (геометрической) оптики, посвященный синтезу оптических систем, состоящих из отдельных и самостоятельных оптических элементов, свойства которых могут быть представлены соответствующими матрицами.

В основе положений матричной оптики лежит принятое в геометрической оптике понятие о световом луче (луче света) , который может быть представлен в виде световой трубки бесконечно малого сечения, т.е. о трехмерной фигуре, в границах которой распространяется энергия излучения, не выходя за ее боковую поверхность и не проникая через нее извне.

Световой луч может быть представлен, также, в виде пучка траекторий световых частиц (фотонов) также имеющего бесконечно малое сечение.Корпускулярная теория света достаточно хорошо объясняет квантовые свойства света (фотоэффект), но не годится для объяснения формы светового луча, что является основной задачей, решаемой в геометрической оптике. В этом случае неизбежно обращение к закономерностям волновой оптики, рассматривающей распространение световой волны и влияние на неё оптической неоднородности среды, обусловленной различной скоростью распространения излучения в различных ее областях, вызванных различиями показателя преломления.

Показателем преломления среды , в которой распространяется излучение, называется отношение скорости света в вакууме к скорости света в данной среде , а именно: . Поскольку скорость света в вакууме представляет собой наивысшую скорость, достигаемую в природе, то показатель преломления любого вещества всегда больше единицы.

Явление замедления света при его распространении в среде непосредственно вытекает из уравнений Максвелла ,учитывающих свойства среды при распространении электромагнитной волны через диэлектрическую постоянную среды и магнитную проницаемость , как: . Многие оптические среды (но не все) не обладают магнитными свойствами, Для нихи потому .

Волновые свойства света в матричной оптике, равно как и вообще в расчётах в геометрической оптике, учитываются неявным образом, через зависимость показателя преломления от длины волны , а точнее — от частоты , связанных между собой соотношением: . Существенно, что длина волны зависит от показателя преломления среды, а частота не зависит. По крайней мере, до тех пор, пока интенсивность света не станет настолько высокой, что начнут сказываться нелинейные эффекты.

Показатель преломления воздуха близок к единице и потому в геометрической оптике по умолчанию считается, что показатель преломления среды, в которой находятся элементы оптической схемы, равен единице. Это неверно в общем случае, например при расположении части или всей оптической системы в среде с n > 1 (так называемая иммерсия). Однако это в случае однородной (изотропной) оптической среды легко может быть учтено при расчётах в рамках геометрической оптики.

В неоднородной оптической среде, с непостоянным в пространстве и времени распределением показателя преломления (или, как говорят,неравномерной оптической плотностью) наблюдаются отступления от прямолинейности распространения света — искривление луча. В неоднородной атмосфере это проявляется в таких явлениях, как мираж, дрожание изображения вследствие атмосферной турбулентности, (что имеет особое значение для оценки качества астроклимата местности) и рассматривается в атмосферной оптике.МО не рассматривает эти проблемы.

В рамках волновой оптики в большом количестве практически интересных случаев направление светового луча совпадает с нормалью к поверхности волнового фронта, т.е. поверхности, проведённой через точки пространства, в которых фазы колебаний электрического вектора совпадают. Однако в случае особых свойств среды, выражающихся в её дихроизме, нормаль к волновому фронту не совпадает с направлением переноса энергии, т. е направлением светового луча. Это явление изучается в кристаллооптике.МО не рассматривает эти проблемы

В большинстве задач прикладной оптики оптические приборы представляют собой совокупность последовательно расположенных оптических элементов с неизменным показателем преломления, который лишь меняется скачком на границе их оптических (т.е. рабочих) поверхностей. Световой луч, в таком случае, представляет собой ломаную линию, состоящую из отрезков прямых. Как правило, несмотря на требуемое по конструктивным соображением весьма сложное расположение оптических элементов в пространстве, оказывается возможным путём использования приёма геометрической развёртки луча , выделить некоторое генеральное направление в виде прямой линии, называемой оптической осью прибора на его схематическом изображени

ru.wikibooks.org

Матричная оптика Википедия

Матричная оптика — математический аппарат расчета оптических систем различной сложности.

Принцип

Пусть известно направление распространения светового луча перед оптической системой. Пусть y1{\displaystyle y_{1}} — «высота» луча над главной оптической осью системы, v1{\displaystyle v_{1}} — приведенный угол: v1=n×α{\displaystyle v_{1}=n\times \alpha }, где α{\displaystyle \alpha } — угол между направлением распространения луча и главной оптической осью системы, n — показатель преломления среды в данной точке. Тогда соответствующие координаты луча после прохождения оптической системы связаны с исходными матричным уравнением:
[y2v2]=[ABCD]×[y1v1]{\displaystyle {\begin{bmatrix}y_{2}\\v_{2}\end{bmatrix}}={\begin{bmatrix}A&B\\C&D\end{bmatrix}}\times {\begin{bmatrix}y_{1}\\v_{1}\end{bmatrix}}},

где [ABCD]{\displaystyle {\begin{bmatrix}A&B\\C&D\end{bmatrix}}} — матрица оптической системы, также именуемая матрица передачи луча.

Определитель матрицы оптической системы равен отношению показателей преломления на входе и на выходе системы, обычно это отношение равно 1. Матричное преобразование — это приближенное линейное описание системы. Оно работает, в частности, когда выполняется параксиальное приближение.

Матрицы простейших оптических систем

Сферическая преломляющая поверхность

M=[10−Φ11]{\displaystyle M={\begin{bmatrix}1&0\\-\Phi _{1}&1\end{bmatrix}}}, Φ1=n2−n1n2∗R{\displaystyle \Phi _{1}={\frac {n_{2}-n_{1}}{n_{2}*R}}}, где n1{\displaystyle n_{1}} и n2{\displaystyle n_{2}} — показатели преломления среды (Подразумевается, что луч переходит из среды с n1{\displaystyle n_{1}} в среду с n2{\displaystyle n_{2}}), R — алгебраический радиус кривизны сферической поверхности (R > 0 для выпуклой поверхности, когда сонаправлены падающий луч и радиус-вектор в центр кривизны поверхности, и R < 0 для вогнутой поверхности).

Сферическое зеркало

M=[10−Φ21]{\displaystyle M={\begin{bmatrix}1&0\\-\Phi _{2}&1\end{bmatrix}}}, Φ2=−2⋅nR{\displaystyle \Phi _{2}=-{\frac {2\cdot n}{R}}}, где n{\displaystyle n} — показатель преломления среды, R — алгебраический радиус кривизны (см. выше).

Трансляция

Трансляцией называется прямолинейное распространение луча между преломлениями/отражениями,например, между двумя линзами.
M=[1T01]{\displaystyle M={\begin{bmatrix}1&T\\0&1\end{bmatrix}}}, T=dn{\displaystyle T={\frac {d}{n}}}, d — длина трансляции, n — показатель преломления.

Применение метода

Итоговая матрица оптической системы есть произведение матриц отдельных простейших элементов, причем в порядке, противоположном порядку этих элементов, т. е. M=Mn×⋅⋅⋅×M2⋅M1{\displaystyle M=M_{n}\times \cdot \cdot \cdot \times M_{2}\cdot M_{1}}, где Mi{\displaystyle M_{i}} — матрица i-того оптического элемента, считая от положения падающего на систему луча.
Оптическая сила оптической системы:
Φ=−C{\displaystyle \Phi =-C}
B=0,y2=A⋅y1{\displaystyle B=0,y_{2}=A\cdot y_{1}} — общее условие формирования изображения в данной точке. В данном случае A есть увеличение системы.

Расчет оптической силы толстой линзы матричным методом

Пусть линза с радиусами кривизны R1,R2{\displaystyle R_{1},R_{2}} (для определенности — двояковыпуклая), толщиной d, из материала с показателем преломления n находится в воздухе. Тогда оптическая система состоит из трех простейших элементов — двух преломляющих поверхностей и трансляции внутри линзы. Имеем:

M1=[10−Φ11]{\displaystyle M_{1}={\begin{bmatrix}1&0\\-\Phi _{1}&1\end{bmatrix}}}
M2=[1T01]{\displaystyle M_{2}={\begin{bmatrix}1&T\\0&1\end{bmatrix}}}
M3=[10−Φ21]{\displaystyle M_{3}={\begin{bmatrix}1&0\\-\Phi _{2}&1\end{bmatrix}}}
Матрица всей оптической системы:
M=M3⋅M2⋅M1=[10−Φ21]×[1T01]×[10−Φ11]=[1−TΦ1TTΦ1Φ2−Φ1−Φ21−TΦ2]{\displaystyle M=M_{3}\cdot M_{2}\cdot M_{1}={\begin{bmatrix}1&0\\-\Phi _{2}&1\end{bmatrix}}\times {\begin{bmatrix}1&T\\0&1\end{bmatrix}}\times {\begin{bmatrix}1&0\\-\Phi _{1}&1\end{bmatrix}}={\begin{bmatrix}1-T\Phi _{1}&T\\T\Phi _{1}\Phi _{2}-\Phi _{1}-\Phi _{2}&1-T\Phi _{2}\end{bmatrix}}}
Отсюда оптическая сила толстой линзы:
Φ=−C=Φ1+Φ2−dΦ1Φ2n{\displaystyle \Phi =-C=\Phi _{1}+\Phi _{2}-{\frac {d\Phi _{1}\Phi _{2}}{n}}}
Для тонкой линзы третьим слагаемым можно пренебречь:
Φ=−C=Φ1+Φ2{\displaystyle \Phi =-C=\Phi _{1}+\Phi _{2}}
С учетом Φ1=n−1R1,Φ2=n−1R2{\displaystyle \Phi _{1}={\frac {n-1}{R_{1}}},\Phi _{2}={\frac {n-1}{R_{2}}}}
, получаем известную формулу для оптической силы линзы: Φ=(n−1)⋅(1R1+1R2){\displaystyle \Phi =(n-1)\cdot ({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}})}.

Литература

• Джеррард А., Бёрч Дж. М. Введение в матричную оптику. М. Мир 1978г. 341с.
• Салех Б.Е.А., Тейх М.К. Оптика и фотоника. Принципы и применения. Пер. с англ.: Учебное пособие. В 2 т. Долгопрудный: Интеллект, 2012. — 1544 с. — Раздел 1.4, стр. 50-68.

wikiredia.ru

Матричная оптика Википедия

Матричная оптика — математический аппарат расчета оптических систем различной сложности.

Содержание

• 1 Принцип
• 2 Матрицы простейших оптических систем
  • 2.1 Сферическая преломляющая поверхность
  • 2.2 Сферическое зеркало
  • 2.3 Трансляция
• 3 Применение метода
• 4 Расчет оптической силы толстой линзы матричным методом
• 5 Литература

Принцип[ | ]

Пусть известно направление распространения светового луча перед оптической системой. Пусть y1{\displaystyle y_{1}} — «высота» луча над главной оптической осью системы, v1{\displaystyle v_{1}} — приведенный угол: v1=n×α{\displaystyle v_{1}=n\times \alpha }, где α{\displaystyle \alpha } — угол между направлением распространения луча и главной оптической осью системы, n — показатель преломления среды в данной точке. Тогда соответствующие координаты луча после прохождения оптической системы связаны с исходными матричным уравнением:
[y2v2]=[ABCD]×[y1v1]{\displaystyle {\begin{bmatrix}y_{2}\\v_{2}\end{bmatrix}}={\begin{bmatrix}A&B\\C&D\end{bmatrix}}\times {\begin{bmatrix}y_{1}\\v_{1}\end{bmatrix}}},

где [ABCD]{\displaystyle {\begin{bmatrix}A&B\\C&D\end{bmatrix}}} — матрица оптической системы, также именуемая матрица передачи луча.

Определитель матрицы оптической системы равен отношению показателей преломления на входе и на выходе системы, обычно это отношение равно 1. Матричное преобразование — это приближенное линейное описание системы. Оно работает, в частности, когда выполняется параксиальное приближение.

Матрицы простейших оптических систем[ |

ru-wiki.ru

Матричная оптика — Википедия. Что такое Матричная оптика

Матричная оптика — математический аппарат расчета оптических систем различной сложности.

Принцип

Пусть известно направление распространения светового луча перед оптической системой. Пусть y1{\displaystyle y_{1}} — «высота» луча над главной оптической осью системы, v1{\displaystyle v_{1}} — приведенный угол: v1=n×α{\displaystyle v_{1}=n\times \alpha }, где α{\displaystyle \alpha } — угол между направлением распространения луча и главной оптической осью системы, n — показатель преломления среды в данной точке. Тогда соответствующие координаты луча после прохождения оптической системы связаны с исходными матричным уравнением:
[y2v2]=[ABCD]×[y1v1]{\displaystyle {\begin{bmatrix}y_{2}\\v_{2}\end{bmatrix}}={\begin{bmatrix}A&B\\C&D\end{bmatrix}}\times {\begin{bmatrix}y_{1}\\v_{1}\end{bmatrix}}},

где [ABCD]{\displaystyle {\begin{bmatrix}A&B\\C&D\end{bmatrix}}} — матрица оптической системы, также именуемая матрица передачи луча.

Определитель матрицы оптической системы равен отношению показателей преломления на входе и на выходе системы, обычно это отношение равно 1. Матричное преобразование — это приближенное линейное описание системы. Оно работает, в частности, когда выполняется параксиальное приближение.

Матрицы простейших оптических систем

Сферическая преломляющая поверхность

M=[10−Φ11]{\displaystyle M={\begin{bmatrix}1&0\\-\Phi _{1}&1\end{bmatrix}}}, Φ1=n2−n1R{\displaystyle \Phi _{1}={\frac {n_{2}-n_{1}}{R}}}, где n1{\displaystyle n_{1}} и n2{\displaystyle n_{2}} — показатели преломления среды (Подразумевается, что луч переходит из среды с n1{\displaystyle n_{1}} в среду с n2{\displaystyle n_{2}}), R — алгебраический радиус кривизны сферической поверхности (R > 0 для выпуклой поверхности, когда сонаправлены падающий луч и радиус-вектор в центр кривизны поверхности, и R < 0 для вогнутой поверхности).

Сферическое зеркало

M=[10−Φ21]{\displaystyle M={\begin{bmatrix}1&0\\-\Phi _{2}&1\end{bmatrix}}}, Φ2=−2⋅nR{\displaystyle \Phi _{2}=-{\frac {2\cdot n}{R}}}, где n{\displaystyle n} — показатель преломления среды, R — алгебраический радиус кривизны (см. выше).

Трансляция

Трансляцией называется прямолинейное распространение луча между преломлениями/отражениями,например, между двумя линзами.
M=[1T01]{\displaystyle M={\begin{bmatrix}1&T\\0&1\end{bmatrix}}}, T=dn{\displaystyle T={\frac {d}{n}}}, d — длина трансляции, n — показатель преломления.

Применение метода

Итоговая матрица оптической системы есть произведение матриц отдельных простейших элементов, причем в порядке, противоположном порядку этих элементов, т. е. M=Mn×⋅⋅⋅×M2⋅M1{\displaystyle M=M_{n}\times \cdot \cdot \cdot \times M_{2}\cdot M_{1}}, где Mi{\displaystyle M_{i}} — матрица i-того оптического элемента, считая от положения падающего на систему луча.
Оптическая сила оптической системы:
Φ=−C{\displaystyle \Phi =-C}
B=0,y2=A⋅y1{\displaystyle B=0,y_{2}=A\cdot y_{1}} — общее условие формирования изображения в данной точке. В данном случае A есть увеличение системы.

Расчет оптической силы толстой линзы матричным методом

Пусть линза с радиусами кривизны R1,R2{\displaystyle R_{1},R_{2}} (для определенности — двояковыпуклая), толщиной d, из материала с показателем преломления n находится в воздухе. Тогда оптическая система состоит из трех простейших элементов — двух преломляющих поверхностей и трансляции внутри линзы. Имеем: M1=[10−Φ11]{\displaystyle M_{1}={\begin{bmatrix}1&0\\-\Phi _{1}&1\end{bmatrix}}}
M2=[1T01]{\displaystyle M_{2}={\begin{bmatrix}1&T\\0&1\end{bmatrix}}}
M3=[10−Φ21]{\displaystyle M_{3}={\begin{bmatrix}1&0\\-\Phi _{2}&1\end{bmatrix}}}
Матрица всей оптической системы:
M=M3⋅M2⋅M1=[10−Φ21]×[1T01]×[10−Φ11]=[1−TΦ1TTΦ1Φ2−Φ1−Φ21−TΦ2]{\displaystyle M=M_{3}\cdot M_{2}\cdot M_{1}={\begin{bmatrix}1&0\\-\Phi _{2}&1\end{bmatrix}}\times {\begin{bmatrix}1&T\\0&1\end{bmatrix}}\times {\begin{bmatrix}1&0\\-\Phi _{1}&1\end{bmatrix}}={\begin{bmatrix}1-T\Phi _{1}&T\\T\Phi _{1}\Phi _{2}-\Phi _{1}-\Phi _{2}&1-T\Phi _{2}\end{bmatrix}}}
Отсюда оптическая сила толстой линзы:
Φ=−C=Φ1+Φ2−dΦ1Φ2n{\displaystyle \Phi =-C=\Phi _{1}+\Phi _{2}-{\frac {d\Phi _{1}\Phi _{2}}{n}}}
Для тонкой линзы третьим слагаемым можно пренебречь:
Φ=−C=Φ1+Φ2{\displaystyle \Phi =-C=\Phi _{1}+\Phi _{2}}
С учетом Φ1=n−1R1,Φ2=n−1R2{\displaystyle \Phi _{1}={\frac {n-1}{R_{1}}},\Phi _{2}={\frac {n-1}{R_{2}}}}
, получаем известную формулу для оптической силы линзы: Φ=(n−1)⋅(1R1+1R2){\displaystyle \Phi =(n-1)\cdot ({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}})}.

Литература

• Джеррард А., Бёрч Дж. М. Введение в матричную оптику. М. Мир 1978г. 341с.
• Салех Б.Е.А., Тейх М.К. Оптика и фотоника. Принципы и применения. Пер. с англ.: Учебное пособие. В 2 т. Долгопрудный: Интеллект, 2012. — 1544 с. — Раздел 1.4, стр. 50-68.

wiki.sc

Матричная оптика — Карта знаний

• Матричная оптика — математический аппарат расчета оптических систем различной сложности.

Источник: Википедия

Связанные понятия

Асфери́ческими называют линзы, одна или обе поверхности которых не являются сферическими.

Подробнее: Асферическая линза

Элементная база оптического приборостроения Как правило, любой оптический прибор состоит из нескольких отдельных оптических элементов, каждый из которых выполняет свою функцию по преобразованию поля излучения. Исключением являются лишь простейшие оптические приборы типа зеркала или увеличительного стекла, представленные одним единственным элементом.Время индивидуального производства осталось в прошлом. Изделия, входящие в эту базу, в подавляющем числе случаев являются предметами серийного или массового… Параксиа́льное приближе́ние в геометрической оптике — рассмотрение только лучей, идущих под малыми углами к главной оптической оси. Параксиальное приближение применимо во многих оптических приборах и существенно упрощает теоретические расчеты. Оптическая система (англ. optical system) — совокупность оптических элементов (преломляющих, отражающих, дифракционных и т. п.), созданная для преобразования световых пучков (в геометрической оптике), радиоволн (в радиооптике), заряженных частиц (в электронной и ионной оптике). Геометрический фактор (также этендю, от фр. étendue géométrique) — физическая величина, характеризующая то, насколько свет в оптической системе «расширен» по размерам и направлениям. Эта величина соответствует параметру качества пучка (BPP) в физике Гауссовых пучков. Ли́нза (нем. Linse, от лат. lens — чечевица) — деталь из прозрачного однородного материала, имеющая две преломляющие полированные поверхности, например, обе сферические; или одну — плоскую, а другую — сферическую. В настоящее время всё чаще применяются и «асферические линзы», форма поверхности которых отличается от сферы. В качестве материала линз обычно используются оптические материалы, такие как стёкла, оптические стёкла, кристаллы, оптически прозрачные пластмассы и другие материалы. Светово́й луч в геометрической оптике — линия, вдоль которой переносится световая энергия. Менее чётко, но более наглядно, можно назвать световым лучом пучок света малого поперечного размера. Геометри́ческая о́птика — раздел оптики, изучающий законы распространения света в прозрачных средах, отражения света от зеркально-отражающих поверхностей и принципы построения изображений при прохождении света в оптических системах без учёта его волновых свойств. Поляриза́ция волн — характеристика поперечных волн, описывающая поведение вектора колеблющейся величины в плоскости, перпендикулярной направлению распространения волны. Абсолютная оптическая система — оптическая система, формирующая стигматическое изображение трёхмерной области. Для формирования стигматического изображения необходимо, чтобы испущенные каждой точкой оптического объекта лучи после прохождения через оптическую систему все пересекались в одной точке. Следовательно, абсолютная оптическая система не нарушает гомоцентричности проходящих через неё световых пучков. Самим названием подчёркивается, что абсолютные оптические системы нельзя реализовать практически… Электростатическая линза — устройство, предназначенное для формирования пучков электронов, их фокусировки и создания электронно-оптических изображений объектов. Более точное определение: линзой является любое аксиально-симметричное поле. Бетатронные колебания — быстрые поперечные колебания, совершаемые частицей в фокусирующих магнитных полях ускорителя. Бетатронные колебания — основной предмет изучения электронной оптики, раздела физики ускорителей. Дифференциальная интерференционно-контрастная микроскопия (интерференционно-контрастная микроскопия или микроскопия Номарского) — световая оптическая микроскопия, используемая для создания контраста в неокрашенных прозрачных образцах. ДИК-микроскоп позволяет определить оптическую плотность исследуемого объекта, используя интерференцию света, и таким образом увидеть недоступные глазу детали. Относительно сложная оптическая система позволяет создать чёрно-белую картину образца на сером фоне. Это изображение…

Подробнее: Дифференциальный интерференционно-контрастный микроскоп

Дифракционная решётка — оптический прибор, действие которого основано на использовании явления дифракции света. Представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья. Эллипсометрия — высокочувствительный и точный поляризационно-оптический метод исследования поверхностей и границ раздела различных сред (твердых, жидких, газообразных), основанный на изучении изменения состояния поляризации света после взаимодействия его с поверхностью границ раздела этих сред. Число Штреля (англ. Strehl ratio) — величина, характеризующая качество оптического изображения, впервые предложенная Карлом Штрелем и названная в честь него. Используется в ситуациях, когда оптическое разрешение ухудшается из-за аберраций в линзе или из-за искажений при прохождении через турбулентную атмосферу. Имеет значение от 0 до 1, при этом в гипотетической идеальной оптической системе число Штреля равно 1. Внешний вид объектов, двигающихся с релятивистской скоростью, существенно зависит от формы объекта и способа его наблюдения. Можно выделить два основных способа: одновременное фиксирование положения точек поверхности и фотографирование при помощи ортогонального или проективного отображения. Составная преломляющая линза — набор одиночных рентгеновских преломляющих линз, обеспечивающих преломление рентгеновских лучей, которые расположены в линейном массиве для достижения фокусировки рентгеновского излучения в диапазоне энергий 2—100 кэВ. Являются перспективным направлением развития современной рентгеновской оптики. Афока́льная опти́ческая систе́ма, телескопи́ческая опти́ческая систе́ма — оптическая система (фокусное расстояние которой неограниченно большое), преобразующая параллельный световой пучок в параллельный же, но с другим углом наклона оптической оси. Предназначена главным образом для наблюдения удалённых объектов. Аксиконус — специализированный тип линзы, у которой одна из сторон имеет коническую форму. Аксиконус — отправная точка для линии, идущей вдоль оптической оси, или для преобразования луча лазера в кольцо. Он может быть использован для преобразования луча Гаусса в приближение к лучу Бесселя с хорошим сокращением дифракции. Эффекти́вная пло́щадь рассе́яния (ЭПР; в некоторых источниках — эффективная пове́рхность рассеяния, эффективный попере́чник рассеяния, эффективная отража́ющая площадь, ЭОП) в радиолокации — площадь некоторой фиктивной плоской поверхности, расположенной нормально к направлению падающей плоской волны и являющейся идеальным и изотропным переизлучателем, которая, будучи помещена в точку расположения цели, создаёт в месте расположения антенны радиолокационной станции ту же плотность потока мощности, что… Преломле́ние (рефра́кция) — изменение направления луча (волны), возникающее на границе двух сред, через которые этот луч проходит или в одной среде, но с меняющимися свойствами, в которой скорость распространения волны неодинакова. Хроматическая поляризация —явление образования окраски у интерференционной картины, формирующейся в результате последовательного прохождения белого света через поляризатор, двупреломляющую прозрачную среду и анализатор. Открыто французским физиком Араго в 1811 году. Параметры Стокса — это набор величин, описывающих вектор поляризации электромагнитных волн, введенный в физику Дж. Стоксом в 1852 году. Параметры Стокса являют собой альтернативу описанию некогерентного или частично поляризованного излучения в терминах полной интенсивности, степени поляризации и формы эллипса поляризации. Кикучи-линия или линия Кикучи (по имени получившего их впервые японского физика Сэйси Кикути — пара полос, образующихся при электронной дифракции от монокристалла. Это явление можно наблюдать при дифракции отражённых электронов в РЭМ и в просвечивающем электронном микроскопе на достаточно толстой для многократного рассеяния области образца. Полосы служат «дорогами в ориентационном пространстве» для микроскопистов, которые не уверены в том, что они наблюдают. В отличие от дифракционных рефлексов… Сфери́ческая аберра́ция — аберрация оптических систем из-за несовпадения фокусов для лучей света, проходящих на разных расстояниях от оптической оси. Приводит к нарушению гомоцентричности пучков лучей от точечного источника, без нарушения симметрии строения этих пучков (в отличие от комы и астигматизма). Различают сферическую аберрацию третьего, пятого и высшего порядков. Дифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы. Отраже́ние — физический процесс взаимодействия волн или частиц с поверхностью, изменение направления волнового фронта на границе двух сред с разными свойствами, в котором волновой фронт возвращается в среду, из которой он пришёл. Одновременно с отражением волн на границе раздела сред, как правило, происходит преломление волн (за исключением случаев полного внутреннего отражения). Аберра́ция оптической системы — ошибка или погрешность изображения в оптической системе, вызываемая отклонением луча от того направления, по которому он должен был бы идти в идеальной оптической системе. Аберрацию характеризуют различного вида нарушения гомоцентричности в структуре пучков лучей, выходящих из оптической системы. Рентгеновская оптика — отрасль прикладной оптики, изучающая процессы распространения рентгеновских лучей в средах, а также разрабатывающая элементы для рентгеновских приборов. Рентгеновская оптика, в отличие от обычной, рассматривает электромагнитные волны в диапазоне длин волн рентгеновского 10−4 до 100 Å (от 10−14 до 10−8 м) и гамма-излучений Диаграмма направленности (антенны) — графическое представление зависимости коэффициента усиления антенны или коэффициента направленного действия антенны от направления антенны в заданной плоскости. Также термин «диаграмма направленности» применим к другим устройствам, излучающим сигнал различной природы, например акустическим системам. Простра́нство предме́тов (нем. Objektraum, англ. Object space, фр. Espace objet) — совокупность возможных положений точек предметов — вершин световых пучков, входящих в оптическую систему. Термин определяется по ГОСТ как «совокупность точек пространства». Бипри́зма Френе́ля — оптическое устройство для получения пары когерентных световых пучков, предложенное Огюстеном Френелем. Бипризма представляет собой две одинаковых треугольных прямоугольных призмы, с очень малым преломляющим углом, сложенные своими основаниями. На практике бипризму обычно изготавливают из пластинки стекла. Поляриметр (полярископ, — только для наблюдения) — прибор, предназначенный для измерения угла вращения плоскости поляризации, вызванной оптической активностью прозрачных сред, растворов (сахарометрия) и жидкостей. В широком смысле поляриметр — это прибор, измеряющий параметры поляризации частично поляризованного излучения (в этом смысле могут измеряться параметры вектора Стокса, степень поляризации, параметры эллипса поляризации частично поляризованного излучения и т.п.). Ко́матическая аберрация или Ко́ма (от др.-греч. κόμη — волосы) — одна из пяти аберраций Зейделя оптических систем, приводящая к нарушению гомоцентричности широких световых пучков, входящих в систему под углом к оптической оси. Опти́ческий пинце́т (англ. optical tweezers), иногда «лазерный пинцет» или «оптическая ловушка» — оптический инструмент, который позволяет манипулировать микроскопическими объектами с помощью лазерного света (обычно испускаемого лазерным диодом). Он позволяет прикладывать к диэлектрическим объектам силы от фемтоньютонов до наноньютонов и измерять расстояния от нескольких нанометров до микронов. В последние годы оптические пинцеты начали использовать в биофизике для изучения структуры и принципа работы… Опти́ческая си́ла — величина, характеризующая преломляющую способность осесимметричных линз и центрированных оптических систем из таких линз. Сканирующая лазерная поляриметрия — метод измерения толщины слоя нервных волокон сетчатки при тестировании глаукомы. При реализации метода используется эффект поляризованного света. Метод изображений (метод зеркальных отображений) — один из методов математической физики, применяемый для решения краевых задач для уравнения Гельмгольца, уравнения Пуассона, волнового уравнения и некоторых других. Шли́рен-ме́тод (от нем. Schlieren — оптическая неоднородность) — способ обнаружения оптических неоднородностей в прозрачных, преломляющих средах, и выявления дефектов отражающих поверхностей. Наземный лазерный сканер (НЛС) — это съёмочная система, измеряющая с высокой скоростью (от нескольких тысяч до миллиона точек в секунду) расстояния от сканера до поверхности объекта и регистрирующая соответствующие направления (вертикальные и горизонтальные углы) с последующим формированием трёхмерного изображения (скана) в виде облака точек.

Подробнее: Наземное лазерное сканирование

Фотометрия (др.-греч. φῶς, родительный падеж φωτός — свет и μετρέω — измеряю) — общая для всех разделов прикладной оптики научная дисциплина, на основании которой производятся количественные измерения энергетических характеристик поля излучения. Сфера Лоренца — метод вычисления локального поля в микроскопической теории диэлектриков. Позволяет найти диэлектрическую проницаемость материала, если известна дипольная поляризуемость частиц материала. Широкую известность получил после выхода в свет классического труда Хендрика Антона Лоренца «Теория электронов и её применение к явлениям света и теплового излучения». Антенная решётка (АР) — сложная антенна, состоящая из совокупности отдельных антенн (излучающих элементов), расположенных в пространстве особым образом. Антенные решётки применяются для повышения коэффициента направленного действия антенны как системы излучающих элементов по сравнению с одиночным элементом и для получения возможности управления формой диаграммы направленности (в том числе, ориентации в пространстве) с помощью электрических сигналов (электрическое сканирование луча в противовес механическому… Интерферо́метр Рэле́я — однопроходной двулучевой интерферометр, разделяющий свет от источника на два потока, разница фаз между которыми создаётся пропусканием света сквозь две одинаковые кюветы, заполненные разными газами. Впервые был предложен лордом Рэлеем в 1886 году. Использовался для определения показателей преломления газов. Интерферометр — измерительный прибор, действие которого основано на явлении интерференции. Принцип действия интерферометра заключается в следующем: пучок электромагнитного излучения (света, радиоволн и т. п.) с помощью того или иного устройства пространственно разделяется на два или большее количество когерентных пучков. Каждый из пучков проходит различные оптические пути и направляется на экран, создавая интерференционную картину, по которой можно установить разность фаз интерферирующих пучков в… Показа́тель рассе́яния — величина, обратная расстоянию, на котором поток монохроматического излучения, распространяющегося в среде в виде параллельного пучка, уменьшается вследствие рассеяния в среде в некоторое заранее оговоренное число раз. В принципиальном плане степень уменьшения потока излучения в данном определении можно выбирать любой, однако в научно-технической, справочной и нормативной литературе и в целом на практике используются два значения степени уменьшения: одно, равное 10 (десятичный… Разреше́ние — способность оптического прибора воспроизводить изображение близко расположенных объектов. Ковариа́нтный метод — подход в теоретической физике, разработанный Ф. И. Фёдоровым на основе линейной алгебры и прямого тензорного исчисления. Получил распространение в приложении к описанию оптических явлений и, частично, в физике элементарных частиц.

kartaslov.ru

Матричная оптика — Howling Pixel

Матричная оптика — математический аппарат расчета оптических систем различной сложности.

Принцип

Пусть известно направление распространения светового луча перед оптической системой. Пусть y1{\displaystyle y_{1}} — «высота» луча над главной оптической осью системы, v1{\displaystyle v_{1}} — приведенный угол: v1=n×α{\displaystyle v_{1}=n\times \alpha }, где α{\displaystyle \alpha } — угол между направлением распространения луча и главной оптической осью системы, n — показатель преломления среды в данной точке. Тогда соответствующие координаты луча после прохождения оптической системы связаны с исходными матричным уравнением:
[y2v2]=[ABCD]×[y1v1]{\displaystyle {\begin{bmatrix}y_{2}\\v_{2}\end{bmatrix}}={\begin{bmatrix}A&B\\C&D\end{bmatrix}}\times {\begin{bmatrix}y_{1}\\v_{1}\end{bmatrix}}},

где [ABCD]{\displaystyle {\begin{bmatrix}A&B\\C&D\end{bmatrix}}} — матрица оптической системы, также именуемая матрица передачи луча.

Определитель матрицы оптической системы равен отношению показателей преломления на входе и на выходе системы, обычно это отношение равно 1. Матричное преобразование — это приближенное линейное описание системы. Оно работает, в частности, когда выполняется параксиальное приближение.

Матрицы простейших оптических систем

Сферическая преломляющая поверхность

M=[10−Φ11]{\displaystyle M={\begin{bmatrix}1&0\\-\Phi _{1}&1\end{bmatrix}}}, Φ1=n2−n1n2∗R{\displaystyle \Phi _{1}={\frac {n_{2}-n_{1}}{n_{2}*R}}}, где n1{\displaystyle n_{1}} и n2{\displaystyle n_{2}} — показатели преломления среды (Подразумевается, что луч переходит из среды с n1{\displaystyle n_{1}} в среду с n2{\displaystyle n_{2}}), R — алгебраический радиус кривизны сферической поверхности (R > 0 для выпуклой поверхности, когда сонаправлены падающий луч и радиус-вектор в центр кривизны поверхности, и R < 0 для вогнутой поверхности).

Сферическое зеркало

M=[10−Φ21]{\displaystyle M={\begin{bmatrix}1&0\\-\Phi _{2}&1\end{bmatrix}}}, Φ2=−2⋅nR{\displaystyle \Phi _{2}=-{\frac {2\cdot n}{R}}}, где n{\displaystyle n} — показатель преломления среды, R — алгебраический радиус кривизны (см. выше).

Трансляция

Трансляцией называется прямолинейное распространение луча между преломлениями/отражениями,например, между двумя линзами.
M=[1T01]{\displaystyle M={\begin{bmatrix}1&T\\0&1\end{bmatrix}}}, T=dn{\displaystyle T={\frac {d}{n}}}, d — длина трансляции, n — показатель преломления.

Применение метода

Итоговая матрица оптической системы есть произведение матриц отдельных простейших элементов, причем в порядке, противоположном порядку этих элементов, т. е. M=Mn×⋅⋅⋅×M2⋅M1{\displaystyle M=M_{n}\times \cdot \cdot \cdot \times M_{2}\cdot M_{1}}, где Mi{\displaystyle M_{i}} — матрица i-того оптического элемента, считая от положения падающего на систему луча.
Оптическая сила оптической системы:
Φ=−C{\displaystyle \Phi =-C}
B=0,y2=A⋅y1{\displaystyle B=0,y_{2}=A\cdot y_{1}} — общее условие формирования изображения в данной точке. В данном случае A есть увеличение системы.

Расчет оптической силы толстой линзы матричным методом

Пусть линза с радиусами кривизны R1,R2{\displaystyle R_{1},R_{2}} (для определенности — двояковыпуклая), толщиной d, из материала с показателем преломления n находится в воздухе. Тогда оптическая система состоит из трех простейших элементов — двух преломляющих поверхностей и трансляции внутри линзы. Имеем:

M1=[10−Φ11]{\displaystyle M_{1}={\begin{bmatrix}1&0\\-\Phi _{1}&1\end{bmatrix}}}
M2=[1T01]{\displaystyle M_{2}={\begin{bmatrix}1&T\\0&1\end{bmatrix}}}
M3=[10−Φ21]{\displaystyle M_{3}={\begin{bmatrix}1&0\\-\Phi _{2}&1\end{bmatrix}}}
Матрица всей оптической системы:
M=M3⋅M2⋅M1=[10−Φ21]×[1T01]×[10−Φ11]=[1−TΦ1TTΦ1Φ2−Φ1−Φ21−TΦ2]{\displaystyle M=M_{3}\cdot M_{2}\cdot M_{1}={\begin{bmatrix}1&0\\-\Phi _{2}&1\end{bmatrix}}\times {\begin{bmatrix}1&T\\0&1\end{bmatrix}}\times {\begin{bmatrix}1&0\\-\Phi _{1}&1\end{bmatrix}}={\begin{bmatrix}1-T\Phi _{1}&T\\T\Phi _{1}\Phi _{2}-\Phi _{1}-\Phi _{2}&1-T\Phi _{2}\end{bmatrix}}}
Отсюда оптическая сила толстой линзы:
Φ=−C=Φ1+Φ2−dΦ1Φ2n{\displaystyle \Phi =-C=\Phi _{1}+\Phi _{2}-{\frac {d\Phi _{1}\Phi _{2}}{n}}}
Для тонкой линзы третьим слагаемым можно пренебречь:
Φ=−C=Φ1+Φ2{\displaystyle \Phi =-C=\Phi _{1}+\Phi _{2}}
С учетом Φ1=n−1R1,Φ2=n−1R2{\displaystyle \Phi _{1}={\frac {n-1}{R_{1}}},\Phi _{2}={\frac {n-1}{R_{2}}}}
, получаем известную формулу для оптической силы линзы: Φ=(n−1)⋅(1R1+1R2){\displaystyle \Phi =(n-1)\cdot ({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}})}.

Литература

• Джеррард А., Бёрч Дж. М. Введение в матричную оптику. М. Мир 1978г. 341с.
• Салех Б.Е.А., Тейх М.К. Оптика и фотоника. Принципы и применения. Пер. с англ.: Учебное пособие. В 2 т. Долгопрудный: Интеллект, 2012. — 1544 с. — Раздел 1.4, стр. 50-68.

Геометрическая оптика

Геометри́ческая о́птика — раздел оптики, изучающий законы распространения света в прозрачных средах, отражения света от зеркально-отражающих поверхностей и принципы построения изображений при прохождении света в оптических системах без учёта его волновых свойств.

Основное понятие геометрической оптики — это световой луч. При этом подразумевается, что направление потока лучистой энергии (ход светового луча) не зависит от поперечных размеров пучка света.

Законы геометрической оптики являются частным предельным случаем более общих законов волновой оптики, в предельном случае стремления длины световых волн к нулю. Так как свет физически является распространением электромагнитной волны, происходит интерференция, в результате которой ограниченный пучок света распространяется не в каком-то одном направлении, а имеет конечное угловое распределение т. е. наблюдается дифракция. Интерференция и дифракция находятся вне предмета изучения оптических свойств оптических систем средствами геометрической оптики. Однако, в тех случаях, когда характерные поперечные размеры пучков света достаточно велики по сравнению с длиной волны, можно пренебречь дифракционной расходимостью пучка света и считать, что лучи света распространяются по отрезкам прямых, до преломления или отражения.

Геометрическая оптика неполно описывает оптические явления, являясь упрощением более общей волновой оптической теории. Но широко используется, например, при расчёте оптических систем, так как её законы математически более просты по сравнению с обобщающими волновыми законами, что существенно снижает математические трудности при анализе и синтезе оптических систем. Приблизительная аналогия между геометрической и волновой оптиками — как между ньютоновской механикой и общей теории относительности.

Помимо пренебрежения волновыми эффектами в геометрической оптике также пренебрегают квантовыми явлениями. В геометрической оптике скорость распространения света считается бесконечной (поэтому динамическая физическая задача превращается в чисто геометрическую), однако учёт конечной скорости света в рамках геометрической оптики (например, в астрофизических приложениях) не представляет математической трудности. Кроме того, как правило, не рассматриваются эффекты, связанные с влиянием прохождения света через оптические среды, например, изменения показателя преломления среды под воздействием мощного излучения. Эти эффекты, даже формально лежащие в рамках геометрической оптики, относят к нелинейной оптике. В случае, когда интенсивность светового пучка, распространяющегося в данной среде, достаточно мала для того, чтобы можно было пренебречь нелинейными эффектами, геометрическая оптика базируется на общем для всех разделов оптики фундаментальном законе о независимом распространении лучей (принцип суперпозиции).

Согласно этому принципу, лучи света в среде не взаимодействуют. В геометрической оптике нет таких понятий, как амплитуда, частота, фаза и вид поляризации светового излучения, но и в волновой линейной оптике постулируют принцип суперпозиции. Иными словами, и в волновой линейной оптике, и в геометрической оптике принимается, что лучи света и оптические волны не влияют друг на друга и распространяются независимо.

This page is based on a Wikipedia article written by authors (here).
Text is available under the CC BY-SA 3.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

howlingpixel.com