Вискозиметр своими руками из шприца: Как определить вязкость краски по DIN своими руками: таблица значений

Содержание

Как определить вязкость краски по DIN своими руками: таблица значений

Чтобы получить красивый слой краски на поверхности, необходимо чтобы состав был нужной степени вязкости. Но что это такое, и как понять, что состояние краски оптимально и ее будет легко распределить на основании? Об этом подробно будет рассказано в статье.

Вязкость лакокрасочных материалов

Чтобы лучше понять, как получить нужную вязкость, необходимо разбираться в факторах, которые оказывают влияние на данный уровень. Вязкость лакокрасочных материалов может изменяться под действием следующих факторов:

Химические элементы, используемые в составе;
Количество растворителя, введённого в состав;
Температурные показатели воздуха, основания и самого лакокрасочного материала.

Выдерживание краской течения во многом зависимо от температурных показателей. Когда произошло нагревание до +60-70 градусов, то параметр сильно понижается, повышение градусов уже незначительно влияет на материал.

Для того чтобы измерить показатель верно, процесс проводится в определенных условиях.

Чтобы улучшить вязкость, применяется добавка разбавителей. Но важно вводить средство в правильном количестве, иначе он может нарушить свойства состава и привести к полной порче.

Чтобы улучшить вязкость, применяется добавка разбавителей.

Что зависит от вязкости

Зачем вообще проводить измерение уровня вязкости, что зависит от показателя? Выделяется влияние параметра на инструмент, которым потребуется наносить краску на поверхность. Будет ли использоваться валик, кисточки или пульверизатор во многом зависит от качества краски. Также влияние параметра существенно в нижеописанных моментах:

Излишне вязкий состав тяжело распределять по поверхности, слой от этого будет толще, а прочность результата пострадает. Также замедлиться просушка слоя;
Густая консистенция не сможет закрыть все мелкие изъяны, впитаться глубже в основание, это приведет к ухудшению уровня сцепляемости;

Толстый слой ведет к появлению подтеков и некрасивому покрытию;
Недорогие пульверизаторы не могут распределять густые составы.

Неподходящая консистенция краски для краскопульта может привести к потребности его разбора и полного очищения, оставшаяся часть просто пропадет. Слишком жидкий состав не сможет прокрашивать поверхность качественно, придется делать больше слоев, повысится расход и время работы, усилий придется приложить больше.

Излишне вязкий состав тяжело распределять по поверхности, слой от этого будет толще, а прочность результата пострадает.

Как измерить вязкость

Определение вязкости российскими производителями выполняется в секундном виде. А зарубежные марки применяют единицу din. Вязкость краски в din таблица есть, которая помогает проверить, какой уровень должен быть у разных составов – акриловых, водоэмульсионных и других.

Засекается время, и оценивают, как быстро краска проходит через специальное отверстие. Чем быстрее это происходит, тем более жидкий состав.

Вязкость краски в din таблица есть, которая помогает проверить, какой уровень должен быть у разных составов.

Особенности измерения

Разница в название единицы в разных странах, никак не влияет на работу специального прибора, который называется вискозиметр. Измеряется параметр по времени, процесс течения состава занимает секунды. И соответственно, чем быстрее она стекает через отверстие определённого размера, тем консистенция более жидкая.

Измеряется параметр по времени, процесс течения состава занимает секунды.

Методы определения вязкости

Стандартно для замеров используется специальный прибор, о котором упоминалось ранее, вискозиметр. Но если его нет в наличии, то может применяться народный способ, визуальной оценки, он не дает такого же точного результата, но может быть вполне приемлемым.

Если вискозиметра нет в наличии, то может применяться народный способ, визуальной оценки.

Определение вязкости вискозиметром

Чтобы применить прибор, следует изучить правила, как пользоваться вискозиметром для краски. Процесс несложный, включает следующие действия:

В специальную ванну, оборудование наливается вода, она помогает сохранять необходимый температурный режим на +20 градусах;
Сопло на вискозиметре закрывается;
Специальный отсек для лакокрасочного материала заполняется, выбранной краской до острия крючков;
Необходимо установить оборудование верно, для этой цели на нем есть винты, которые позволяют отрегулировать положение, острые части крючков должны ставиться в едва заметном положении и быть на одной плоскости;
Закрывается отсек с краской, в специальную дырочку вставляют термометр, сопло пока не открывают, и ставится вблизи мензурка;

При достижении лакокрасочного материала нужного температурного показателя в +20 градусов, и появлении пузырьков, сопло можно будет открыть и начать считать секунды, завершается счет после набора в емкость состава на уровне 50.

Если работа будет вестись с густыми типами материалов, то применяется шариковый тип вискозиметра. Его принцип измерения предполагает подсчет секунд прохождения шариков по вертикали.

Если работа будет вестись с густыми типами материалов, то применяется шариковый тип вискозиметра.

«Народный метод» измерения вязкости («на глаз»)

Данная методика зависит от опыта мастера, профессионалы могут визуально понять, насколько краска хорошо будет распределяться по поверхности. Краску размешивают с помощью палки из дерева или металла. После вынимают палочку, чтобы посмотреть, как быстро состав будет стекать. И оценивают степень густоты.

Умельцы сделали вискозиметр для краски своими руками, для этого просто нужно взять шприц, и отрезать его до размера в 10 мм, также отрезается половина нижнего конца. Наливается средство, и засекается время стекания.

Вынимают палочку, чтобы посмотреть, как быстро состав будет стекать.

В каких единицах измеряется

На российском рынке принято за единицу измерения вязкости лакокрасочных материалов принимать секунды. Иностранные бренды, например, такие, как Белинка, указывают данный параметр на упаковке в виде DIN.

На российском рынке принято за единицу измерения вязкости лакокрасочных материалов принимать секунды.

Оборудование для вязких материалов

Если материал отличается вязким свойством, то обычно ее наносят с помощью пульверизаторов. Для этой цели подходят разные виды пульверизаторов. Можно выделить следующие варианты:

Безвоздушный тип, в котором насос выталкивает сразу краску, не используя воздуха. Его эффективность использования краски высока, но цена также высокая, поэтому выбирается чаще профессионалами;

Пневматический, который работает с помощью создания давления воздухом. Более доступный тип.

Если материал отличается вязким свойством, то обычно ее наносят с помощью пульверизаторов.

Вязкость водоэмульсионной краски

Вязкость водоэмульсионной краски, если учитывать российскую единицу, то должна составлять в среднем значении минимальное 40, максимально 45 секунд, когда используются ручные способы нанесения. Для пульверизатора показатель будет другим: 20-25 секунд. Вязкость водоэмульсионной краски в din имеет примерно те же значения, лишь меняется обозначение.

Вязкость водоэмульсионной краски должна составлять в среднем значении минимальное 40, максимально 45 секунд.

Особенности определения вязкости краски для краскопульта

Процесс определения уровня для нанесения краски пульверизатором не отличается от измерения для кисточек и валиков. Важно сравнивать, получаемый параметр по таблице в соответствующей инструменту графой. Ведь для пульверизаторов требуется создавать более жидкую консистенцию.

Для пульверизаторов требуется создавать более жидкую консистенцию.

Какие значения считаются оптимальными

Каждый производитель может указывать свой параметр вязкости, который будет необходим. Это значение может быть прописано на этикетке продукта. Либо можно будет узнать его на сайте компании. Есть единая таблица со средними показателями, она также поможет в данном вопросе.

Каждый производитель может указывать свой параметр вязкости, который будет необходим.

Если краска будет разбавлена до нужной вязкости, то получить качественный результат будет проще. Определять его значение легко, и процесс не занимает много времени. Особенно важно учитывать вязкость для работы с пульверизатором.

Видео: Как определить вязкость краски

виды дефектов при покраске автомобиля

Осматривая окончательный результат покраски своего автомобиля, владельцы могут быть сильно разочарованы. Потратив огромное количество средств и времени, они, в конечном счете, могут увидеть возникновения на свежо нанесенном лакокрасочном покрытии, различного рода дефектов. Виной всему — непрофессионализм маляра. Из-за нехватки опыта, при подготовке к покраске, во время нее или после, были допущены грубые ошибки. Составим небольшой перечень факторов возникновения дефектов на лакокрасочных покрытиях.

Хлопья — широко известный дефект, возникающий при смешивании несовместимого с краской растворителя. В результате, окрас сворачивается в так называемые «хлопья», далее является непригодным.
Подтеки — причиной может быть очень жидкий или толстый слой краски. Низкая температура детали, воздуха, неправильное расстояние между распылителем и деталью, неравномерное поглощение лака и др.
Зернистость — источником могут послужить твердые частицы краски, которые не отфильтровали, осевшая на свежую краску пыль. Ошибка маляра в выборе слишком большого расстояния распылителя к детали.
Шагрень — внешне напоминает апельсин. Вызван дефект неправильным подбором разбавителя, разбавитель слишком быстро испаряется или не соблюдены пропорции при разбавлении лака. Распылитель плохо распыляет, выбрано неправильное расстояние до окрашиваемой детали, температура в помещении выше, чем температура детали. Не соблюдение интервалов между напылением слоев, краска распыляется очень обильно.
Отслаивание лака — происходит из-за остатков былой краски или ржавчины. Нижний слой краски не совместим с лаком, не использовалось защитное покрытие.
Лак, завивается — деталь покрыта сильно толстым слоем краски, нижняя часть не просыхает. Покрытие не сохнет из-за низких температур, нанесен толстым слоем или не подходит по типу. На местах где использовалась шпаклевка, могут появляться матовые пятна.
Изменение цвета — может происходить, если маляр не провел испытания с образцом перед сушкой, начинает темнеть. Выбраны не подходящие по качеству компоненты. Может светлеть если нагревательные элементы сушки стоят слишком близко.
Кратеры на поверхности краски — происходят при перегреве растворителя, сушильные элементы стоят сильно близко, не была проведена предварительная сушка детали. Машина стояла в пыльном месте, была применена полироль, в состав которой входят силикаты.
Матовый оттенок — может вызвать влажный воздух. Ярко выражено проявляется с прихотливыми красками синих и красных тонов. Не просушенный воздух в помещении может приводить к появлению кратеров на верхней части детали. Порой появлению погрешностей может способствовать человеческая халатность по отношению к красящему оборудованию (компрессора, сушильной камере или распрыскивателю).
Дефекты, возлагающиеся на производителя — могут послужить различная вязкость краски. Попадание других смесей из плохо очищенной тары. Чаще всего, неисправность оборудования является первопричиной различного рода дефектов.
Изношенность деталей краскопульта: изъяны, в результате которых, забиваются воздушные отверстия. Игла имеет явно выраженные повреждения, нет возможности закрыть сопло краскопульта, в результате краска будет не равномерно распыляться и капать.
В результате, от таких повреждений пленка наносимого материала ложится не равномерно. Появляется матовость, подтеки или шагрени.
Плохая работа компрессора не выдает необходимого давления на выходе краскопульта. Результат — невозможно провести покраску автомобиля.
Нет необходимых условий для покраски автомобиля
Плохая вентиляция помещения чревата своими последствиями, в результате повышенной влажности краска может тускнеть.
Из-за неплотного прилегание воздушного фильтра в камере для сушки, поток воздуха протекает неверно. Существует вероятность попадания пыли на свежеокрашенные детали, которые станут неудовлетворительным результатом.
Стоящие датчики в боксе для сушки тоже могут привести к нарушению покраски. Смотря на показания различных датчиков, к примеру: (манометров, термометров и вискозиметров) можно вовремя предотвратить сбои в работе осушительной камеры.
Немаловажным компонентом для покраски является воздух. Его подачу нужно соответственно обеспечить компрессором, манометром, сушилкой, регулятором давления, отводом конденсата воды и фильтром для масляных выделений.

Дефекты из-за несоблюдения требований указанных в инструкции

Дефекты в виде сморщивания выявляются при не соблюдении предписанной инструкции процесса. Чаще всего такого рода дефекты появляются при смешивании компонентов различных производителей. Например, ошибкой при покраске является использование «нитро» как универсального разбавителя. При не соблюдении материалов производителя могут появиться следующие дефекты: закипание, сморщивание, матовый эффект, шагрень т. п.

Готовим поверхность к покраске

Сначала очищают поверхность детали, которую будут красить. Каждую деталь основательно высушивают. В противном случае вас ждут дефекты в виде кратеров, растекание краски или же появление пузырей.
Составим список рекомендаций по очистке поверхности. Соблюдая которые можно избежать дальнейших появлений дефектов на лакокрасочном покрытии автомобиля.

Нужно убрать следы ржавчины и грязь. Обезжириваем доступными средствами и высушиваем. Дополнительное время уделяем кромкам. К подготовленной детали нельзя прикасаться.
Очищаем деталь до основания.
Температура окружающего пространства должна быть не ниже 18°С.
Обращайте внимание на воздух из компрессора, он должен быть сухой.
В помещении для покраски автомобиля, а также сушки, должны стоять фильтры против пыли, отвода воздуха и пара.
Дважды защищаем детали от коррозии.
Новые слои краски наносим только после высыхания предыдущего.
Выполняем инструкцию к вязкости.

Во избежание дефектов, четко соблюдайте инструкции указанные производителем.
Удачи!

Уральский следопыт | Уральский следопыт

1983 06 июнь

Авторы: Белов Василий, Зигуненко Станислав

читать

Подсказывает жизнь
— Николай Николаевич, посмотрите, что я придумал!..
Н, Н. Гришечко извинился за прерванную беседу и ушел посмотреть, что же там такое сотворил изобретатель десяти лет от роду.
Нет, вы не думайте, что слово «изобретатель» тут надо обязательно брать в кавычки. Ребята из кружка изобретателей и рационализаторов Ворошиловградской областной станции юных техников изобретают серьезные вещи. Доказательство тому — авторские свидетельства, дипломы, которые красуются на стенах. И вот этот инструмент, который лежит сейчас перед нами на столе,— фасонные щипцы. Предназначены они для открывания медицинских флаконов. Тех самых, крышечки которых обязательно придерживаются сверху колпачками из алюминиевой фольги. Начнешь сдирать эту крышечку ножницами или каким другим малопригодным для этого инструментом, не успеешь глазом моргнуть — раз! — уже порезался. А сколько таких флаконов в день приходится открывать, скажем, медицинским сестрам в больнице?..
Вот ребята и пришли на помощь взрослым — сконструировали щипцы, для которых открыть любой флакон с лекарством еще проще, чем Щелкунчику раскусить орех. Фасонные губки плотно охватывают крышку, а специальный выступ-зуб тотчас сдирает фольгу. Получается и быстро, и безопасно.
Женя Хорошевский, Юра Краев и другие ребята сделали несколько таких щипцов для местной больницы, и медики остались ими очень довольны.
И это не единственная разработка кружковцев. Они предложили оригинальное устройство для сбора камней с поля, приспособление для очистки льда с рельсов на железнодорожных путях, маленький приборчик для проверки лампочек в елочной гирлянде и устройство для измерения вязкости жидкости в потоке…
Интересно, а откуда ребята берут темы для своих разработок?. Именно этот вопрос мы и задали вернувшемуся к столу Николаю Николаевичу.
— Как это откуда? — удивился он.— Да поглядите вокруг, таких тем сколько угодно в жизни!
И действительно, все получается именно так. Мама, которая работает медицинской сестрой, подсказала одному из кружковцев необходимость фасонных щипцов. Летом поехали в подшефный колхоз — убедились в необходимости устройства для сбора камней. Были на железнодорожной станции — узнали, что зимой стрелки заносит снегом и их приходится чистить вручную.
Да что говорить! Тему для изобретения можно отыскать даже в обычном школьном учебнике.
Вместе с Н. Н. Гришечко — инженером-конструктором и рационализатором, работающим на Ворошиловградском тепловозостроительном заводе, в работе кружка принимает участие и председатель общественного совета ВОИР Ворошиловградской области, кандидат технических наук А. X. Теплицкий.
И вот однажды, зайдя на одно из занятий кружка, Теплицкий напомнил ребятам историю, которая произошла несколько лет назад. Тогдашние кружковцы Анатолий Кубаш и Сергей Пожаров вместе со своими руководителями усовершенствовали конструкцию всем известного вискозиметра — прибора для измерения вязкости жидкости.
Обычно вязкость жидкости оценивают по скорости падения шарика в стеклянной трубке. Чем медленнее падает шарик, тем, значит, больше вязкость. Время падения засекают с помощью секундомера, а затем ведут вычисления по специальным таблицам. «А что если усовершенствовать эту конструкцию? — задумались ребята.— Неужели так уж обязательно все операции проводить вручную, да еще каждый раз отбирать для оценки вязкости специальную пробу. Нельзя ли вести измерения непосредственно в потоке?..»
Оказалось — можно. Прямую трубку заменила v-образная. Вместо одного шарика стало два — один падал по потоку жидкости, другой — против. Таким образом удалось нейтрализовать скорость самого потока. А система катушек индуктивности позволила засекать время падения каждого шарика автоматически, не прибегая к ручному секундомеру.
Эта разработка кружковцев была признана изобретением, на которое выдано настоящее авторское свидетельство.
— Не хотите ли повторить успех своих старших товарищей? — предложил в заключение своего рассказа А. X. Теплицкий.
Конечно, захотели многие. Но повезло пока что одному Саше Крохмалю. Да и то, как сказать — повезло? Просто Саша оказался очень пытливым и наблюдательным человеком.
Рисунок, который натолкнул его на изобретение, и вы наверняка видели. А то, может, и саму модель в руках не раз держали. Я говорю о модели молекулярного строения вещества, которая есть почти в каждом школьном кабинете физики. Помните, несколько цветных, шариков, соединенных между собой спицами? Вот это та самая модель и есть.
Модель как модель. И мы такую в руках не раз держали. Но вот чтобы усовершенствовать… А Саша усовершенствовал. И помог ему в этом… велосипедный насос!
— Вернее, старый медицинский шприц, который я попросил у бабушки. Она у меня врачом работает,— уточняет Саша.— Хотя и насос на том же принципе работает, но у него зазоры между стенками цилиндра и поршнем велики…
Вот этой самой парой — цилиндр-поршень — Саша и предложил заменить традиционную спицу модели. И все!.. Казалось бы, невелико усовершенствование, но какие значительные выгоды оно принесло! Модель из статической, на которую и посмотреть-то интересно всего лишь раз, стала динамической, способной моделировать некоторые процессы из жизни кристалла.
Вот упругие деформации. Вы чуть растянули шарики, поршень двинулся по цилиндру, а воздушное разрежение его не пускает. Стоит только отпустить руки, и поршень тотчас возвращается на место.
Когда же упругие деформации переваливают некоторый предел, кристалл деформируется, связи в нем нарушаются. И это тоже можно продемонстрировать на модели.
Продолжайте растягивать шарики до тех пор, пока поршень не дойдет до отверстия, специально для этого сделанного в цилиндре. Под поршень тотчас же прорвется наружный воздух, и сопротивления как не бывало — упругие деформации сменились пластическими.
А чтобы можно было вернуть модель в исходное состояние, у дна цилиндра предусмотрено еще одно отверстие, закрытие выпускным клапаном.
Вот, собственно, и все. Просто? Да. Только никто до этого раньше не додумался. А потому авторское свидетельство за изобретение демонстрационной модели кристалла совершенно справедливо получил Саша Крохмаль.
Что же касается его товарищей по кружку, то у них первые изобретения пока еще впереди. Но они не унывают. Жизнь продолжается, и каждый день приносит что-то новое и интересное.

Две лучше, чем одна
Так считает москвич Сергей Шубнов. А речь здесь идет о кабинах портального крана.
По своей конструкции такой кран представляет собой своеобразный мост, перекинутый через грузовую площадку от одной опоры к другой. Под мостом перемещается тележка, на которой закреплен грузоподъемный крюк. А сам кран перемещается на тележках по рельсовым путям.
Вот Сережа и предлагает:
— Чтобы крановщику было удобно работать, давайте снабдим кран двумя кабинами, по одной на каждой стороне. Тогда ему будет сподручнее наблюдать за всем, что делается на грузовой площадке.
А чтобы убедиться в правильности своей идеи, Сергей Шубнов построил действующую модель такого крана. Управляется она дистанционно, с помощью выносного пульта.

Роторно-лонаточный комбайн
Полностью он называется так — роторно-лопаточный комбайн с виброфрезой для уборки картофеля, редиски, свеклы и других подобных культур. А изобрел его Максим Ларкин, который живет в Новосибирском Академгородке и там же занимается в местной станции юных техников.
Хотя Максим горожанин, он знает, насколько трудно бывает убирать урожай колхозникам вручную, рот и предложил новую машину для механизации этой трудоемкой операции. В отличие от ныне существующих машин этот комбайн не пашет, не роет землю, а фрезерует ее. Такой способ намного облегчает работу, а если учесть еще, что фреза при работе еще и вибрирует, становится понятно, почему затраты энергии у нового комбайна будут намного меньше. Ведь не случайно в наши дни виброинструментом пользуются работники самых разных специальностей — шахтеры, бурильщики, граверы, даже хирурги. Ультразвуковой виброинструмент в самый твердый материал входит, как нагретый нож в сливочное масло.

«Цып-цып-цып, мои цыплятки!»
Вячеслав Бозаджи из Молдавии тоже решил заняться проблемами сельского хозяйства. Но он не стал строить действующую модель, как это сделали Максим Ларкин или Сергей Шубнов. Он построил самый настоящий автоматический инкубатор!
Размеры его невелики — такой инкубатор вполне размещается на любом столе. Но в нем есть все, что положено иметь настоящему инкубатору — решетка для яиц, обогреватель и автоматические приборы, строго следящие за поддержанием необходимой температуры и влажности.
Работает «Холужок» — так назвал Вячеслав свой инкубатор — от обычной электросети и может найти себе применение в каждом сельском доме.

В помощь школе
И уж, конечно, ребята не обошли своим вниманием школьные нужды. В Ташкенте было представлено большое количество демонстрационных приборов, которые позволяют сделать школьные уроки интереснее, а проводимые опыты — наглядными и познавательными.
Вот, например, бакинец Олег Безенков нашел способ как сделать наглядными даже уравнения Максвелла! Помните, те самые, которые утверждают, что магнитное поле превращается в электрическое и наоборот?
— Но ведь все электромагнитные колебания, за исключением световых, невидимы,— скажете вы.— О какой же наглядности в данном случае может идти речь?
Что нельзя увидеть, то можно услышать. Ведь работают же электромагнитные волны в обычном радиодинамике? Вот на этой остроумной догадке и построена модель Олега.
Прибор возбуждает электрическое поле — раздается звук одного тона. Как только электрическое поле превратилось в магнитное, меняется и тон звукового сопровождения.

читать

Комментарии:

ВКонтакте (0)

Facebook (X)

Обычные (0)

Учебная работа по физике «Вязкость жидкости»

Конкурс

«Пермский университет – школьникам: физико-математические науки»

16 лет

с. Березовка

МБОУ «Березовская СОШ№2»,

9класс

ФИО участника:

Радостев Тимофей Николаевич

Почтовый адрес:

617570 Пермский край,с. Березовка,ул.Труда,4а кв.18

Название работы:

Горизонты науки

Телефон:

89194654115

e-mail:

[email protected]

Научный руководитель:

Дёмина Галина Ивановна

Телефон:

89082630535

e-mail:

[email protected]

«Горизонты науки»

МБОУ «Берёзовская средняя

общеобразовательная школа №2»,

ученик 9 «в» класса.

Руководитель: Дёмина Г.И.

учитель физики высшей кв. кат.

МОУ «Берёзовская средняя

общеобразовательная школа №2».

с. Березовка 2015г.

Оглавление

Введение…………………………………………………………………………………………………….3

Глава 1. Гидродинамика. Уравнение Бернулли .. ……………………….………6

Глава 2. Ламинарное и турбулентное течение жидкости ..…….………….…..10

Глава 3. Коэффициент вязкости. Закон Ньютона ……. ………………………12

Глава 4. Вязкость крови …………………………….……………………..….…14

Глава 5. Неньютоновская жидкость………………………………………….…16

Глава 6. Метод Стокса для определения коэффициента вязкости…………………………………………………………………………..17

Глава 7.Практическая часть……………………………………………….………20

Определение давления жидкости внутри трубки переменного сечения (экспериментальное подтверждение уравнения Бернулли).
Определение коэффициента вязкости глицерина методом Стокса.

Заключение……………………………………………………………………….25

Список литературы……………………………………………………………….27

Введение

Многим известно имя английского ученого – И.Ньютона. Прежде всего, говорят о Ньютоне как о создателе классической механики. Этот человек открыл закон всемирного тяготения, открыл законы разложения белого света и выдвинул корпускулярную теорию света, открыл закон охлаждения нагретого тела, сконструировал один из первых термометров, впервые построил отражательный телескоп.

Именно Ньютон разработал могучий метод математического исследования природы, что оказало огромное влияние на все последующее развитие физики как науки.

При подготовке сообщения о Ньютоне только в одной книге я встретил информацию о том, что он открыл закон сопротивления движению в вязкой жидкости. Меня заинтересовал этот вопрос, и в своей работе я решил изучить закономерности движения жидкости, закон сопротивления движению в вязкой жидкости, подробнее познакомиться со свойством жидкости – ее вязкостью.

Цель работы: изучение закономерностей движения жидкости.

Задачи:

Найти в различных источниках информации законы движения жидкости, сведения о свойствах жидкостей, в частности ее вязкости;
Изучить особенности ньютоновской и неньютоновской жидкостей;
Исследовать явления, происходящие с неньютоновской жидкостью;
Определить экспериментальным способом вязкость жидкости;
Показать практическое проявление движущихся потоков жидкости;

В книге Ф. М. Дягилева «Из истории физики и жизни ее творцов» рассказывается о жизни и творчестве выдающихся физиков. В ней отмечено, что выдающимся трудом И. Ньютона являются «Математические начала натуральной философии». Во второй части «Начал» (иногда так называют) Ньютон рассмотрел силы сопротивления среды при движении в ней тел, гидро- и аэродинамику, простейшие случаи вихревых движений. Эта информация побудила меня изучить движение жидкостей и закономерности, происходящие в ней.

В учебнике И.К. Кикоина «Физика, учебник для 9 класса» раскрывается суть закона Бернулли. В учебнике Г.Я. Мякишева «Физика. Механика.10кл. учебник для углубленного изучения физики» рассмотрены основы гидродинамики: виды движений в жидкости, течение вязкой жидкости, существование силы сопротивления при движении тел в жидкостях. В справочнике школьника Т.И. Трофимовой :Физика от А до Я кратко, но доступно дается материал по вязкости жидкости: определение вязкости жидкости, формула силы внутреннего трения, зависимость вязкости от температуры.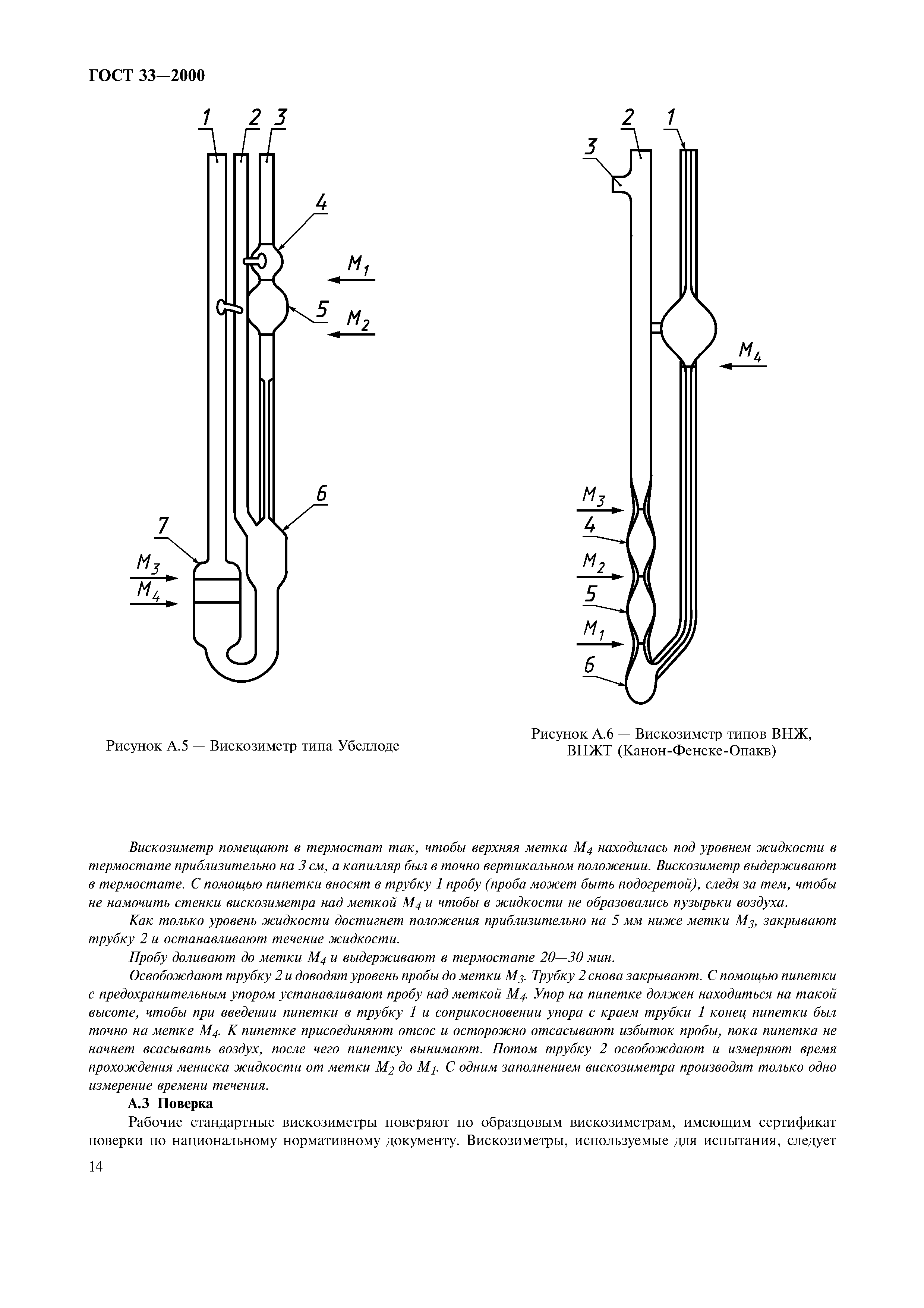

В книге Майорова А.Н. «Физика для любознательных, или о чем не узнаешь на уроке» приведены примеры проявления уравнения Бернулли.

В пособии Г.Е.Кирко «Лабораторные работы» описан метод Стокса для определения коэффициента вязкости.

На сайтах http://www.youtube.com/watch?v=f2XQ97XHjVwhttp://studopedia.ru содержится информация о удивительной жидкости — неньютоновской жидкости.

С движущимися потоками жидкости мы часто встречаемся в технике, быту и в природе. По трубам водопровода течет вода в домах, в машинах подается масло для смазки, по трубам нефтепроводов течет нефть. Кровообращение у человека и животных – это движение крови по трубам – кровеносным сосудам. Даже движение воды в реках можно считать движением жидкости по трубам, если считать русло реки «трубой».

Раздел физики, изучающий движения жидкостей, взаимодействие движущихся жидкостей с твердыми телами называется гидродинамикой.

В общем случае движения жидкости нужно учитывать наличие сил внутреннего трения или вязкости. Вязкость – одно из важнейших явлений, наблюдающихся при движении реальной жидкости. Явления, связанные с вязкостью усложняют исследование движения жидкости. Поэтому полезно вначале отвлечься от усложнений, вносимых ею в картину движения жидкостей и изучить закономерности для идеальной жидкости. Идеальная жидкость — жидкость, вязкостью которой можно пренебречь.

Основным законом гидродинамики является закон (уравнение) Бернулли.

Гидродинамика. Уравнение Бернулли.

Закон (уравнение) Бернулли является следствием закона сохранения энергии для потока идеальной (то есть без внутреннего трения) жидкости:

ρ — плотность жидкости,

v — скорость потока

h — высота, на которой находится рассматриваемый элемент жидкости,

p — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

g — ускорение свободного падения.

Описать движение жидкости трудновато. Хотя гидродинамика основана на трех хорошо знакомых в механике законах сохранения массы, импульса и энергии, их формулировка в данной теме немного сложнее. Например, определение закона сохранения массы обычно выглядит так: масса системы тел остается неизменной. Для жидкости, текущей в трубе, этот закон используется в форме (называемой уравнением неразрывности ):

υS=const

Здесь – υ скорость жидкости, S – площадь сечения трубы, по которой течет жидкость. Сформулировать этот закон можно так: сколько вливается жидкости в трубу, столько должно и выливаться, если условия течения не изменяются. Согласно уравнению неразрывности, скорость жидкости в узких местах трубки больше, чем в широких.

Каково распределение давления в движущейся жидкости? Можно определить его экспериментально. Возьмем трубку переменного сечения с небольшими отверстиями в стенке, в которые вставлены стеклянные открытые сверху измерительные трубки. При стационарном течении (движение жидкости называется стационарным, если во всех точках пространства скорости элементов жидкости не меняются со временем) жидкость в каждой измерительной трубке поднимется до определенной высоты. По высоте столба жидкости в измерительных трубках можно судить о её давлении на стенки горизонтальной трубки. Опыт показывает, что в широких местах трубки, давление больше, чем в узких. Но чем больше сечение трубки, тем меньше скорость течения жидкости. Следовательно, можно сделать вывод:

при стационарном течении жидкости давление больше в тех местах, где меньше скорость течения, и, наоборот, меньше в тех местах, где скорость течения больше.

Зависимость давления идеальной жидкости от скорости ее стационарного течения и перепада высоты была установлена в математической форме Даниилом Бернулли в 1783 году. Уравнение Бернулли выражает закон сохранения энергии и условие неразрывности течения идеальной жидкости.

Уравнение Бернулли просто объясняет множество явлений, происходящих в жидкости.

1) Осенью 1912г. океанский пароход «Олимпик» плыл в открытом море, а почти параллельно ему, на расстоянии 100 метров, проходил с большой скоростью другой корабль, гораздо меньший, броненосный крейсер «Гаук».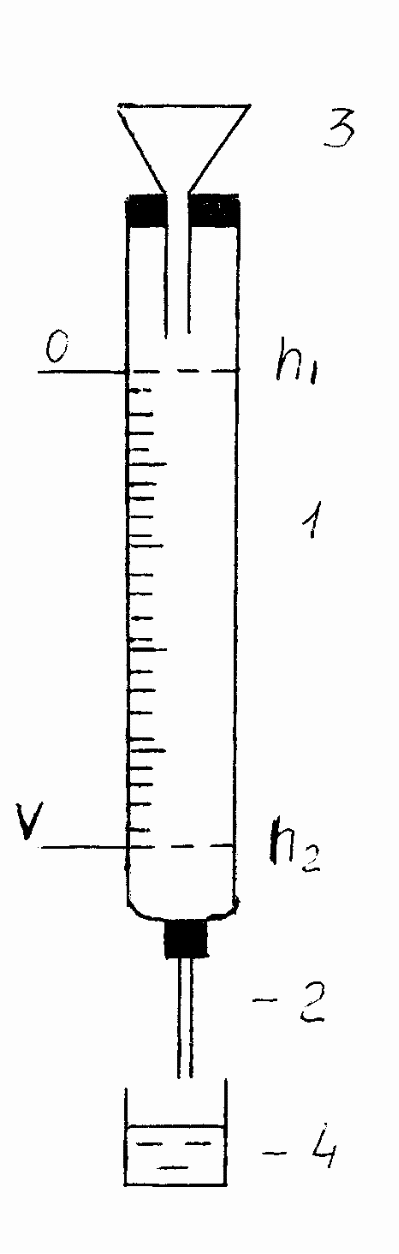 Вдруг произошло нечто неожиданное: меньшее судно стремительно свернуло с пути, словно повинуясь неведомой силе, повернулось носом к большому кораблю и , и не слушаясь руля, двинулось прямо на него. «Гаук» врезался носом в бок «Олимпика». Удар был так силен, что. «Гаук» проделал в борту «Олимпика» большую пробоину. Случай столкновения двух кораблей рассматривался в морском суде. Капитана «Олимпика» обвинили в том, что он не дал команду пропустить броненосец. Не сразу поняли, как можно объяснить происшедшее.

Теперь капитаны морских и речных судов прекрасно знакомы с коварным проявлением уравнения Бернулли. Если два корабля идут параллельным курсом слишком близко один к другому, возникает гидродинамическая сила, толкающая их друг к другу, в результате чего может произойти кораблекрушение. Формула Бернулли позволяет понять, почему возникает эта сила: относительная скорость воды между судами будет больше, чем снаружи, давление воды на корабли в пространстве между ними окажется ниже, чем извне. Перепад давлений по разные стороны кораблей создает силу, толкающую их друг к другу.

2) Закон Бернулли позволяет измерять скорость движения жидкости с помощью манометра – прибора для измерения давления.

3)С помощью уравнения Бернулли можно найти скорость истечения идеальной жидкости из отверстия, расположенного в сосуде на глубине h относительно поверхности жидкости. Если сосуд широкий, а отверстие мало, то скорости жидкости в сосуде малы. Ко всему потоку жидкости в целом можно применить уравнение Бернулли. В верхнем сечении у поверхности жидкости давление p 0 равно атмосферному, а скорость υ0 »0. В нижнем сечении «трубки» — в отверстии давление также равно атмосферному.

4)Ярким примером, где применяется уравнение Бернулли в настоящее время, является «брандспойт». Он устроен так, что его края разного диаметра. Большим диаметром брандспойт цепляется к шлангу по которому подается вода . Она проходит через брандспойт и выходит через отверстие с меньшим диаметром. Получается, проходит через трубку с переменным сечением, где и работает закон Бернулли. За счет этого удалось добиться того, что вода выходит из него с большей скоростью и струя бьет на большие расстояния. Что значительно помогает при тушении пожаров.

По видам движение делится на ламинарное и турбулентное.

Наиболее простым является ламинарное (без завихрений) движение жидкостей. Турбулентное движение наиболее часто встречается, но в реальных жидкостях очень сложно. До сих пор нет полной теории его, хотя проблемы турбулентности изучаются уже более ста лет.

Ламинарное и турбулентное течение жидкости.

Ламинарное (слоистое) – движение жидкости, при котором отдельные слои ее скользят друг относительно друга, не перемешиваясь. Турбулентное (вихревое) – движение жидкости, сопровождающееся перемешиванием ее различных слоев с образованием завихрений. Другими словами: если жидкость находится между двумя металлическими пластинами, то течение жидкости называется ламинарным, когда слой жидкости, контактирующий с подвижной металлической пластиной, имеет ту же скорость, что и эта пластина. Слой жидкости, расположенный ниже, перемещается немного медленнее, и скорость каждого последующего слоя немного меньше, чем предыдущего. При этом каждый слой жидкости скользит по-другому, и разные слои не перемешиваются.

В ламинарном потоке каждая частица жидкости следует по пути своей предыдущей частицы. Скорость течения в любой точке жидкости остается постоянной. Линии тока не пересекаются между собой. Энергия, сообщаемая жидкости для поддержания ее течения, используется, главным образом, на преодоление вязких сил между слоями жидкости.

Другой тип течения называется турбулентным. Турбулентное течение неустойчиво. Послойный характер течения жидкости нарушается. В потоке образуются местные завихрения, частицы перемещаются не только параллельно, но и перпендикулярно оси трубки, непрерывно перемешиваясь. Линии тока становятся искривленными. Скорость частиц, пересекающих конкретную точку жидкости, не является постоянной по направлению и величине: она изменяется со временем. Описание турбулентного потока должно быть статистическим: с точки зрения средних величин. Для турбулентного течения необходима большая энергия, чем для ламинарного, поскольку при турбулентном течении существенно возрастает внутреннее трение между частицами жидкости.

Характер течения будет определяться целым рядом факторов: вязкость жидкости, сечение трубы, скорость течения и плотность жидкости.

На любой малый объем жидкости в потоке действует ускоряющая сила F₁ и сила вязкого трения F₂ . Английский физик Рейнольдс исследовал условия, при которых течение является ламинарным или турбулентным. Переход из ламинарного течения в турбулентное зависит от значения безразмерной величины, называемой числом Рейнольдса. Число Рейнольдса для жидкости, текущей в цилиндрической трубке определяется уравнением: Re = vDρ/η,

где v — средняя скорость потока, D — диаметр трубки, η — вязкость, и ρ — плотность жидкости.

Критическая величина числа Рейнольдса для цилиндрических трубок, при котором ламинарное течение становится турбулентным — 2000 — 2400.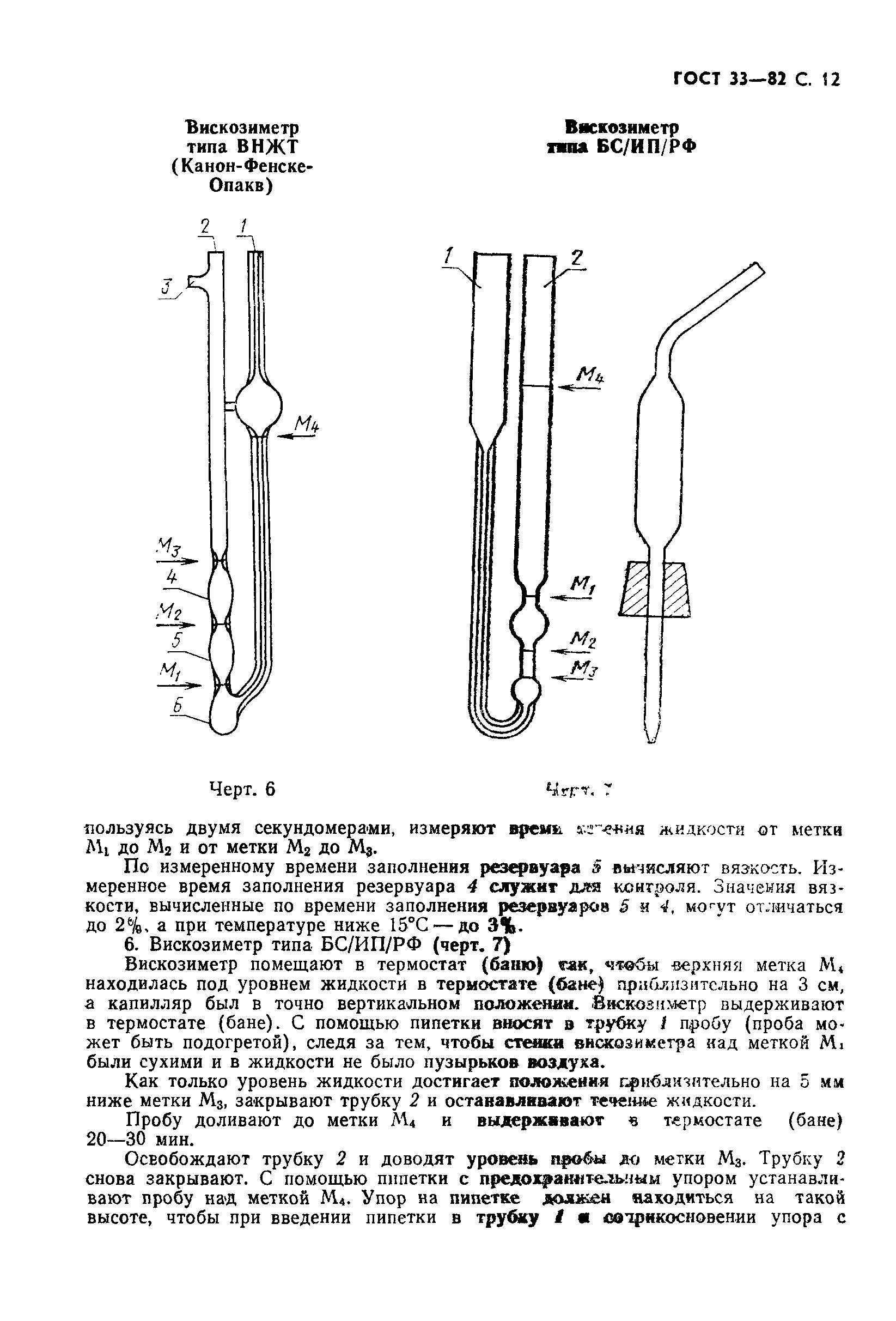

Критическая скорость — скорость жидкости, при превышении которой ламинарное течение переходит в турбулентное. Течение крови в сосудах является ламинарным (за исключением аорты). В аорте наблюдается турбулентное течение крови во время физической работы, которая приводит к существенному увеличению скорости течения крои. Поток крови также может стать турбулентным в артериях при уменьшении площади их поперечного сечения вследствие патологических процессов. Причиной этого феномена является повышение скорости течения крови.

Течение крови в сосудах носит в норме ламинарный характер, небольшая турбулентность наблюдается вблизи клапанов сердца. Турбулентность в крови можно обнаружить по характерным шумам и использовать в диагностике заболеваний.

Если при движении существенным является трение, то вся теория гидродинамики усложняется. При движении жидкости нужно учитывать наличие сил внутреннего трения или вязкости. Вязкость – одно из важнейших явлений, наблюдающихся при движении реальной жидкости. Явления, связанные с вязкостью усложняют исследование движения жидкости.

Коэффициент вязкости. Закон Ньютона.

Вязкость – это одно из явлений переноса, свойство жидкости оказывать сопротивление перемещению одной их части относительно другой.

Всем реальным жидкостям в той или иной степени присуща вязкость, или внутреннее трение. При течении реальной жидкости между ее слоями возникают силы трения. Эти силы получили название сил внутреннего трения или вязкости. Вязкость – это трение между перемещаемыми относительно друг друга слоями жидкости. Силы вязкости (внутреннего трения) направлены по касательной к соприкасающимся слоям жидкости и противодействуют перемещению этих слоев относительно друг друга. Они тормозят слой с большей скоростью и ускоряют медленный слой. Можно указать две основные причины, обусловливающие вязкость:

во-первых, силы взаимодействия между молекулами соприкасающихся слоев, движущихся с различными скоростями;

во-вторых, переход молекул из слоя в слой и связанный с этим перенос импульса.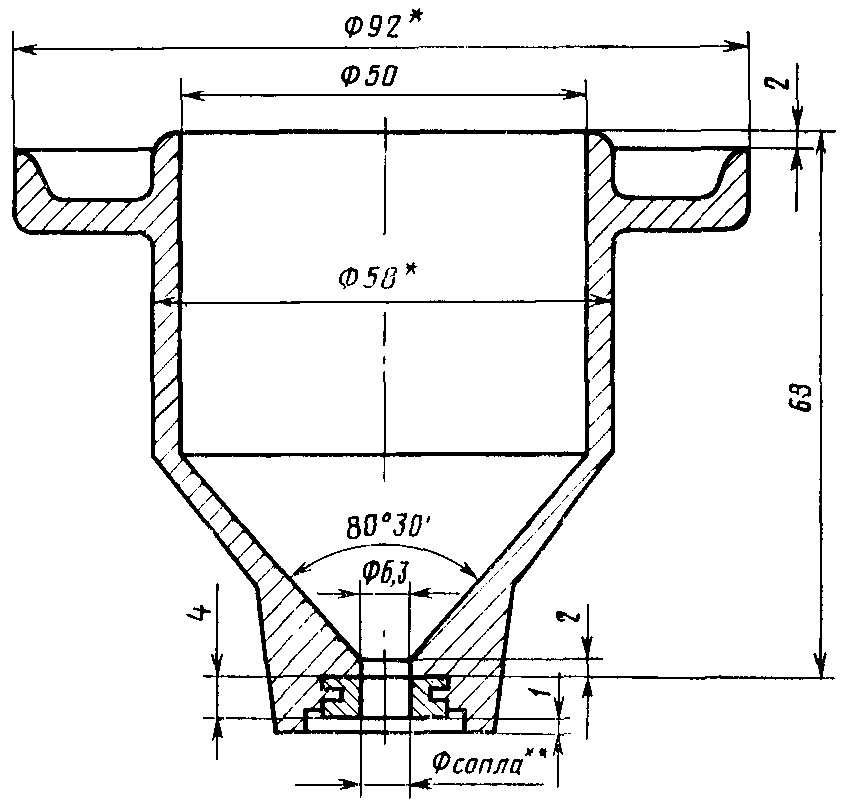

Вследствие этих причин слои взаимодействуют друг с другом, медленный слой ускоряется, быстрый замедляется. В жидкостях ярче выражена первая причина, в газах – вторая.

Ньютон установил, что сила трения между двумя слоями жидкости прямо пропорциональна площади соприкосновения слоев и величине:

— величина, показывающая, как быстро меняется скорость при переходе от слоя к слою.

Эта формула (1)называется формулой Ньютона для вязкого трения. Коэффициент пропорциональности получил название коэффициента вязкости (внутреннего трения).

Жидкости, для которых выполняется формула Ньютона (1), называют ньютоновскими. Для таких жидкостей коэффициент вязкости зависит только от температуры. К ньютоновским жидкостям можно отнести плазму крови.

Для многих реальных жидкостей соотношение (1) строго не выполняется. Такие жидкости называют неньютоновскими. Для них коэффициент вязкости зависит от температуры, давления и ряда других величин. К таким жидкостям относятся жидкости с крупными сложными молекулами, например, цельная кровь, водный раствор крахмала.

В системе СИ единицей измерения коэффициента вязкости является

(паскаль – секунда),

в СГС – системе коэффициент вязкости измеряется в (пуазах), причем

Как отмечено выше, жидкости различают: ньютоновские, неньютоновские. Из биологических к ньютоновским жидкостям относится кроме плазмы крови лимфа.

Закон Ньютона для жидкости применяется в медицине – в лабораториях определяют вязкость крови для выяснения на содержание эритроцитов, общего содержания белка и соотношения его фракций в плазме, а также содержания в крови углекислоты. Повышение вязкости отмечается при сгущении крови и некоторых видах лейкозов (эритремии, миелофиброзах), понижение — при анемиях.

Вязкость крови

Кровь является взвесью клеток крови в жидкости сложного состава, называемой плазмой. Различают красные клетки крови (эритроциты), белые клетки крови (лейкоциты) и тромбоциты. Плазма — водный раствор электролитов, белков, питательных веществ, продуктов метаболизма и т. п. Объем крови в организме составляет почти 7% объема человеческого тела. Эритроциты занимают около 45 % объема крови, а другие клетки крови — менее чем 1%. Относительный объем клеток крови и плазмы определяют с помощью прибора гематокрита. Это же название используют для определения результатов анализа.

Кровь является более плотной и вязкой, чем вода. В среднем относительная вязкость крови составляет почти 4,5 (3,5-5,4). Относительная вязкость плазмы — 2,2 (1,9 — 2,6). Вязкость крови измеряется в лаборатории с помощью специального прибора — медицинского вискозиметра. Кровь является неньютоновской жидкостью. Но при такой скорости течения, которая поддерживается в сосудах кровеносной системы, вязкие свойства крови можно рассматривать, как для ньютоновских жидкостей. А плазма крови – ньютоновская жидкость.

Вязкость крови зависит, главным образом, от концентрации эритроцитов и меньше — от концентрации белков плазмы. Она зависит также от скорости течения крови. Если скорость течения крови уменьшается, эритроциты собираются в специфические скопления, так называемые монетные столбики. Это приводит к повышению вязкости крови. Такой феномен может наблюдаться в мелких кровеносных сосудах, где скорость течения крови небольшая.

Однако существует физиологический механизм, который способствует уменьшению вязкости крови в небольших сосудах, называемый эффектом Фареуса-Линдквиста. Этот эффект объясняется ориентацией эритроцитов вдоль оси сосуда. Эритроциты, формируя цилиндрический осевой ток, скользят по слою окружающей их плазмы крови.

Вязкость крови здорового человека , при патологии колеблется от , что сказывается на скорости оседания эритроцитов. Вязкость венозной крови больше, чем артериальной.

Кроме практического применения вязкости в жидкости меня удивило поведение неньютоновской жидкости.

Неньютоновская жидкость

Можно ли ходить по воде? С точки зрения физики невозможно, но это только в том случае, если речь не идет о неньютоновской жидкости. Что это за жидкость и почему по ней можно ходить, я бы хотел рассказать и объяснить в своей работе.

Ньютоновская жидкость (названная так в честь Исаака Ньютона) — вязкая, подчиняющаяся в своём течении закону вязкого трения Ньютона, жидкость. Неньютоновская жидкость — это особенная, чрезвычайно непонятная и удивительная субстанция. Загадочность такой жидкости заключается в том, что при сильном воздействии на нее, она сопротивляется словно твердое тело, в то же время, при медленном – приобретает жидкие свойства. В отличие от однородной ньютоновской, она имеет неоднородную структуру и состоит из крупных молекул. Ньютоновские и неньютоновские жидкости в последнее время вызывают активный интерес не только ученых, но и простых людей. Это связано с тем, что неньютоновская жидкость легко изготавливается своими руками и подходит для домашних опытов

В своей НИЛ я решил провести опыт с неньютоновской жидкостью, и для этого я:

смешал крахмал (250 гр.) и воду (100гр.) в глубокой тарелочке, для того чтобы увидеть удивительные свойства неньютоновской жидкости
Перемешал ингредиенты до образования однородной массы.
После этого из полученной жидкости я попытался скатать маленький шарик. Тут я заметил, что в том случае, если катать шарик очень быстро, то он будет тверже и прочнее. Если прекратить скатывать такой шарик, то он растечется по руке.
Если аккуратно опустить палец в неньютоновскую жидкость, то он без сопротивления войдет во внутрь нее, т.е. она ведет себя как жидкость; но если резко ударить кулаком по ее поверхности, то он встретит твердый отпор.

Это все объясняется тем, что частицы крахмала набухают в воде и между ними формируется физические контакты в виде хаотических сплетенных групп молекул. Эти прочные связи называются зацеплениями. При резком воздействии прочные связи не дают молекулам сдвинуться с места, и система реагирует на внешние воздействия, как упругая пружина. При медленном же воздействии молекулы успевают растянуться и распутаться, сетка рвется и молекулы равномерно расходятся. Если в опыте взять более большой объем этой жидкости и пробежаться по ней человеку, то он теоретически не утонет и продолжит движение по ней, как по твердому телу.

Итак, я могу сделать такое умозаключение, что по поверхности жидкости можно не только ходить, но и даже танцевать. Главное помнить, что неньютоновская жидкость- твердая только тогда, когда есть движение. Стоит остановиться, сразу утонешь. Итак, по жидкости ходить возможно!

Наша кровь — это тоже типичная неньютоновская жидкость. Она представляет собой суспензию эритроцитов, лейкоцитов и других элементов в плазме. А это значит, что вязкость в различных участках сосудистой системы может изменяться.

Сила жидкого трения (сила сопротивления) возникает и при движении твердого тела в жидкости. Благодаря тому, что сила сопротивления растет с увеличением скорости, любое тело в вязкой среде при действии на него какой-либо постоянной силы, например силы тяжести, в конце концов, начинает двигаться равномерно. Такое движение было предложено использовать для определения коэффициента вязкости.

Метод Стокса для определения коэффициента вязкости

Английским физиком и математиком Стоксом было установлено, что сила вязкого трения Fс, действующая в жидкости на движущееся тело, при небольших скоростях прямо пропорциональна скорости, т. е.

где r — коэффициент сопротивления, зависящий от размеров и формы тела, а также от вязкости среды, в которой оно движется.

Для твёрдого тела шарообразной формы радиуса R, движущегося в жидкости с коэффициентом вязкости, коэффициент сопротивления

r = 6.

Тогда по закону Стокса для модуля силы сопротивления, действующей на шарообразное тело, можно записать выражение

Fc=6

Метод Стокса позволяет определить вязкость жидкости.

На шар B массой m, объёмом V, падающий в жидкости с коэффициентом вязкости , действуют три силы: сила тяжести выталкивающая сила (сила Архимеда) и сила сопротивления (рис.1).

Сила тяжести рассчитывается по формуле

Fт= mg=V·

Рис.1

где плотность шара, g – ускорение свободного падения.

Силу Архимеда можно рассчитать, как

здесь m_ж – масса жидкости, вытесненной шаром, плотность этой жидкости. Сила сопротивления Fc вычисляется по формуле (22). Так как сила и постоянны, а сила возрастает с увеличением скорости движения шара, то с некоторого момента времени эти три силы могут уравновесить друг друга. Движение шара станет равномерным. В векторной форме закон движения шара запишется в виде

, или через модули сил этот закон можно записать таким образом: F_т= Fа+ Fс.

Подставив в последнее уравнение выражения для сил и получим

откуда после соответствующих преобразований получается выражение

или, учитывая, что где D- диаметр шара, последнюю формулу можно записать в виде

Практическая часть

Экспериментальное подтверждение уравнения Бернулли.

Для определения давления жидкости внутри трубки переменного сечения я решил использовать медицинские шприцы различной вместимости. Чтобы узнать давление в каждом из участков конструкции я врезал вертикально вверх трубки с небольшим диаметром, в роли которых использовал тоже шприцы. Когда жидкость протекала по моей конструкции, во врезанные трубки тоже попадала вода. И уже наглядно было видно, как изменяется давление в зависимости от диаметра трубки, по которой течет жидкость. В горизонтальном шприце с самым большим сечением столбик воды в вертикальной трубке поднимался на большую высоту, что означает – давление здесь больше. В узких местах трубы высота столбика воды меньше, чем в широких, следовательно скорость движения воды больше.

2. Определение коэффициента вязкости методом Стокса.

Приборы и принадлежности: мензурка, дробинки, микрометр, секундомер, линейка, термометр, резинки (кольцевые метки).

Цель работы: определение вязкости жидкости и характера ее изменения при увеличении температуры.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Измерить расстояние l между кольцевыми метками на цилиндре с исследуемой жидкостью (верхняя метка соответствует положению шара, при котором скорость его становится постоянной).

2. Микрометром измерить диаметры D пяти шаров (дробинок), данные занести в таблицу.

3. Для каждого шара определить время падения ti и скорость падения Vi= l/t между метками. Результаты занести в таблицу.

4. Рассчитать коэффициент вязкости жидкости по движению каждого из шаров. Для этого формулу перепишем в виде

, где к -постоянная в условиях опыта величина

Значение занести в таблицу, вычислить среднее арифметическое значение коэффициента вязкости :

Поскольку коэффициент вязкости зависит от температуры, то эксперимент по его определению проводил при различной температуре: в учебной аудитории, на холоде и в бане.

Выполнение работы.

Определение вязкости при комнатной температуре.

Определил температуру в комнате термометром. Результат t=22⁰C;
Для каждого шара определил время падения ti и скорость падения Vi между метками. Результаты записал в таблицу;
Далее нашел величину k по формуле. Плотности тела и исследуемой жидкости я узнал в табличном справочнике, где плотность дроби 6300 кг/м³, а плотность глицерина 1260 кг/м³.В итоге k=2744. Затем уже рассчитал коэффициент вязкости жидкости по движению каждого из шаров также по формуле. Результаты вычислений вы также можете увидеть в таблице ниже.

Таблица результатов измерений и вычислений при t=22⁰С

опыта

D_i, м

t_i, с

V_i, м/c

Ŋ_i, 10^-3Па·с

0,004

0,28

1568

0,004

2,96

0,29

1513

0,004

2,89

0,294

1493

0,004

3,12

0,27

1626

0,004

2,92

0,291

1508

Также, в конце своего опыта я рассчитал среднее арифметическое значение коэффициента вязкости при t=22⁰С. ŋ_ср = 1568+1513+1493+1626+1508/5= 1541 10^-3Па·с
Затем я сравнил результат эксперимента со значением из табличного справочника. В справочном материале я нашел, что коэффициент вязкости глицерина при 20⁰С равен 1480 •10^-3Па·с. Результат в ходе эксперимента мною был получен 1541• 10^-3Па·с, но у меня температура была чуть больше, значит можно заявить, что коэффициенты очень близки по значению.

Определение вязкости на холоде.

Определил температуру на улице термометром. Результат t=0⁰C;
Для каждого шара определил время падения ti и скорость падения Vi между метками. Результаты можно увидеть в таблице;
Далее найдем величину k по формуле. Плотности тела и исследуемой жидкости я узнал в табличном справочнике, где плотность дроби 6300 кг/м³, а плотность глицерина 1260 кг/м³.В итоге k=2744. Затем уже рассчитал коэффициент вязкости жидкости по движению каждого из шаров также по формуле. Результаты вычислений вы также можете увидеть в таблице ниже.

Таблица результатов измерений и вычислений при t=0⁰c

опыта

D_i, м

t_i, с

V_i, м/c

Ŋ_i, 10^-3Па·с

0,004

0,0369

11901

0,004

22,92

0,037

11862

0,004

23,5

0,036

12195

0,004

22,81

0,0372

11802

0,004

23,2

0,0366

11996

Также, в конце своего опыта я рассчитал среднее арифметическое значение коэффициента вязкости при t=0⁰С. ŋ_ср = 11901+11862+12195+11802+11996/5= 11951 10^-3Па·с
Затем я решил сравнить свой результат со значением из табличного справочника. В справочном материале я нашел, что коэффициент вязкости глицерина при 0⁰С = 12100 10^-3Па·с, мой же результат равен 11951 10^-3Па·с. Отсюда следует, что результаты близки по значению. Поэтому опыт проделан правильно.

Определение вязкости в бане

Определил температуру в бане термометром. Результат t=60⁰C;
Для каждого шара определил время падения ti и скорость падения Vi между метками. Результаты можно увидеть в таблице;
Далее нашел величину k по формуле. Плотности тела и исследуемой жидкости я узнал в табличном справочнике, где плотность дроби 6300 кг/м³, а плотность глицерина 1260 кг/м³.В итоге k=2744. Затем уже рассчитал коэффициент вязкости жидкости по движению каждого из шаров также по формуле. Результаты вычислений вы также можете увидеть в таблице ниже.

Таблица результатов измерений и вычислений при t=60⁰c

опыта

D_i, м

t_i, с

V_i, м/c

Ŋ_i, 10^-3Па·с

0,004

1,94

0,438

100

0,004

2,2

0,386

113

0,004

0,425

103

0,004

1,87

0,45

0,004

2,13

0,39

112

Также, в конце своего опыта я рассчитал среднее арифметическое значение коэффициента вязкости при t=0⁰С. ŋ_ср = 100+113+103+97+112/5= 105 10^-3Па·с
Затем я решил сравнить свой результат со значением из табличного справочника. В справочном материале я нашел, что коэффициент вязкости глицерина при 60⁰С = 102 10^-3Па·с, мой же результат равен 105 10^-3Па·с. Отсюда следует, что результаты близки по значению. Поэтому опыт проделан правильно.

Коэффициент вязкости жидкости сильно зависит от температуры помещения, где проводится опыт.

Вывод: Чем больше температура жидкости , тем меньше коэффициент ее вязкости и наоборот.

Заключение

Изучение движения жидкостей имеет важное значение для практического применения. Движение жидкости подчиняется закону (уравнению) Бернулли. Уравнение Бернулли связывает давление внутри жидкости с площадью поперечного сечения потока жидкости и скорость движения жидкости. Формула Бернулли позволяет понять, почему возникает гидродинамическая сила и позволяет измерить скорость движения жидких тел. Уравнение Бернулли позволяет понять сущность многих явлений. Например, почему есть вероятность сталкивания двух барж, кораблей, проплывающих близко друг к другу.

Течение жидкостей может быть ламинарным и турбулентным.

Если при движении существенным является трение, то вся теория гидродинамики усложняется. Поэтому при движении жидкости необходимо учитывать наличие сил внутреннего трения или вязкости. Из-за вязкости давление в жидкости уменьшается вдоль потока даже в горизонтально расположенной трубе постоянного сечения. Вязкость возникает, потому что силы взаимодействия между соприкасающимися слоями движутся с различными скоростями и переход молекул из слоя в слой связан с переносом импульса.

Сила жидкого трения (сила сопротивления) возникает и при движении твердого тела в жидкости. Благодаря тому, что сила сопротивления растет с увеличением скорости, любое тело в вязкой среде при действии на него какой-либо постоянной силы, например силы тяжести, в конце концов начинает двигаться равномерно. Это учитывается в методе Стокса для определения коэффициента вязкости жидкостей.

С помощью метода Стокса я измерил вязкость глицерина.

Вязкость жидкости зависит от ее температуры. Чем больше температура жидкости, тем меньше коэффициент ее вязкости, и наоборот.

Выполняя работу, я узнал, какие жидкости являются ньютоновскими, какие неньютоновскими.

Ньютоновские жидкости имеют широкое применение в практике и имеют немаловажное значение, неньютоновские же жидкости используются в основном ради забавы и для интересных опытов.

Знания этого раздела применяются в медицине – в лабораториях определяют вязкость крови для выяснения на содержание эритроцитов, общего содержания белка и соотношения его фракций в плазме, а также содержания в крови углекислоты. Повышение вязкости отмечается при сгущении крови и некоторых видах лейкозов (эритремии, миелофиброзах), понижение — при анемиях.

Выполняя исследовательскую работу, я понял, что выбрал именно ту тему, которая мне интересна. И выполнял ее с увлечением. Я расширил свой кругозор, и теперь могу своим сверстникам рассказать о законе сопротивления движению в вязкой жидкости Ньютона, который в школьной программе основной школы не изучается.

Я выполнил задачи, которые ставил перед собой.

Применения знаний этого раздела в различных областях современной науки и техники, биологии и медицины являются, безусловно, актуальными.

Список литературы

И.К. Кикоин «Физика – учебник для 9 класса»: Просвещение, 1990.
Г.Я. Мякишев «Физика. Механика, учебник для 10 класса» – М.: Дрофа, 2013.
Майоров А.Н. «Физика для любознательных, или о чем не узнаешь на уроке»: Академия, К^о, 1999.
Г.Е.Кирко Лабораторные работы
Т.И. Трофимова. Физика от А до Я. – 2-е изд.,-М.:Дрофа,2007.-299с.
Ф.М. Дягилев. Из истории физики и жизни ее творцов: книга для учащихся. – М.:Просвещение,1986. -255с.

Интернет — ресурсы

Смазка и смазочные материалы электрокаров

Категория:

Электрокары

Публикация:

Смазка и смазочные материалы электрокаров

Читать далее:

Смазка и смазочные материалы электрокаров

Своевременная и качественная смазка узлов электрокаров и автопогрузчиков обеспечивает их безотказную работу и долговечность.

Смазочные материалы применяются в соответствии с инструкциями заводов-изготовителей.

Перед смазкой следует тщательно очистить масленки, крышки, пробки и т. п. от грязи во избежание ее попадания в механизмы.

Рекламные предложения на основе ваших интересов:

Смазочные материалы, применяемые для смазки электрокаров и автопогрузчиков, делятся на минеральные масла и консистентные (густые) смазки.

‘ Масла при нормальной температуре (20 °С) представляют собою жидкости с различной степенью текучести и относятся к жидким смазкам.

Консистентные смазки при той же температуре находятся в полутвердом состоянии. Они изготовлены из минеральных масел, загущенных мылами или твердыми углеводородами — парафином, церезином, петролатумом.

В зависимости от состава мыла консистентные смазки разделяются па кальциевые, натриевые, смешанные кальциево-натриевые и др. Смазки, загущенные твердыми углеводородами, называются углеводородными.

Кальциевые консистентные смазки содержат в своем составе некоторое количество свободной и связанной воды и не растворяются.

При нагреве до 55—60 °С эти смазки разлагаются на масло и мыло, но после охлаждения не восстанавливают свои смазочные свойства.

Натриевые; смазки обладают более высокой температурой плавления, застывая после расплавления, они восстанавливают свойства и могут опять применяться. В воде эти смазки легко растворяются и образуют эмульсию, которая легко смывается с поверхности металла.

Кальциево-натриевые смазки применяют при повышенной температуре и небольшой влажности.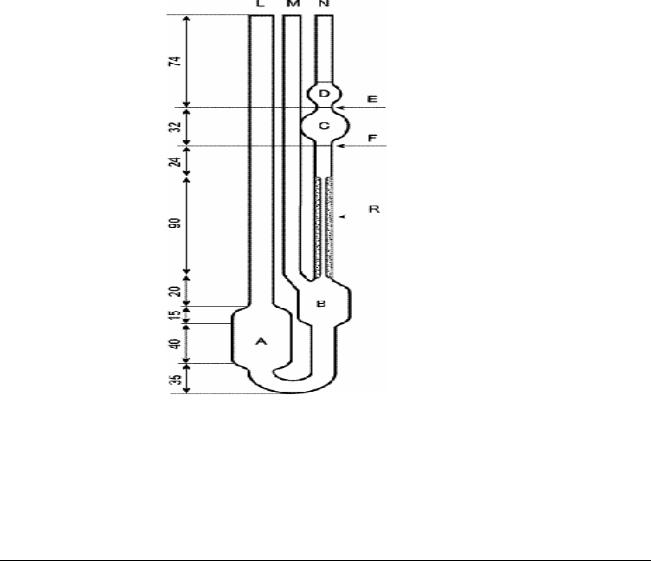 морские и смазки различного назначения.

Консистентные смазки условно обозначаются начальными буквами слов, указывающих свойства смазок или их назначение: У — универсальная; И — индустриальная; В — водостойкая; М — морозостойкая; К — канатная; Н — низкоплавкая; С — сред-неплавкая; Т — тугоплавкая.

Масла и смазки в зависимости от сорта и марки отличаются Друг от друга своими физико-химическими свойствами, которые устанавливаются и гарантируются Государственными общесоюзными стандартами (ГОСТ). Важнейшие свойства масел и смазок приводятся ниже.

Основными характеристиками масел являются их вязкость и температура вспышки. Вязкостью называется внутреннее трение, возникающее между молекулами жидкости при относительном перемещении их под действием внешней силы. Различают вязкость динамическую, кинематическую и условную.

Динамическую и кинематическую вязкость определяют капиллярными вискозиметрами.

Условная вязкость по ГОСТ 6258—52 определяется отношением времени истечения из вискозиметра типа ВУ испытываемого масла в количестве 200 мл (см3) к времени истечения такого же количества дистиллированной воды при температуре 20 °С.

Условная вязкость выражается в градусах ВУ50 или ВУ100 , где индекс 50 или 100 обозначает температуру масла при испытании.

Вязкость масла изменяется в зависимости от температуры. При повышении температуры вязкость уменьшается, при понижении — увеличивается.

В стандартах вязкостно-температурная характеристика масла дается числовой величиной, получаемой от деления числовых значений кинематической вязкости при температурах 50 и 100 °С.

Температурой вспышки масла называют температуру, при которой пары масла, нагретого в установленных стандартом условиях, образуют с окружающим воздухом смесь, вспыхивающую при поднесении к ней пламени. Эта температура определяет способность масла к испарению и характеризует.его огнеопасность. Само масло при определении температуры вспышки еще не загорается.

Температура, при которой не только вспыхивают масляные пары, но загорается само масло и горит не менее 5 сек., называется температурой воспламенения масла. Температура застывания масла характеризует потерю его текучести при низкой температуре, когда масло после наклонения стандартной пробирки под углом 45° остается неподвижным в течение 1 мин. Наиболее высокую температуру застывания (+17 °С) имеет масло цилиндровое 38, а самую низкую (—60 °С) — масло приборное МВП.

Кислотное число выражает количество миллиграммов едкого калия, требующееся для нейтрализации 1 г масла, и характеризует содержание в маслах органических кислот, присутствие которых в количествах выше 0,35% может вызвать коррозию металла, соприкасающегося с таким маслом. В масле не должно быть воды, и масло считается безводным, если в нем воды меньше 0,025%.

Механические примеси, находящиеся в масле во взвешенном состоянии, вызывают повышенный износ машин и засорение маслопроводов. Стандартами допускается наличие механических примесей в масле в количестве, не превышающем 0,007%.

Консистентные смазки характеризуются температурой капле-падения, при которой происходит падение первой капли смазки, нагреваемой в определенных условиях в особом приборе.

Рис. 76. Пресс-масленки:
а — запрессованная; б — без переходного штуцера; в — с переходным штуцером.

Рис. 77. Шприцы для консистентной смазки.

Чем выше температура каплепадения смазки, тем выше и допустимая температура ее работы. Наиболее высокую температуру каплепадения (200 °С) имеет смазка НК-50. Пенетрация характеризует степень густоты смазки, ее плотность и определяется пенетрометром по глубине погружения в смазку стандартного конуса при температуре 25 °С в течение 5 сек. Чем мягче смазка, тем глубже в нее погружается конус. По числу пенетрации можно примерно судить о пригодности смазки для выбранного способа ее подачи через масленки и трубы.

Для кальциевых смазок обязательной составной частью является вода в количестве не выше 3%, для натриевых — не выше 0,5%, в предохранительных смазках воды не должно быть. Свободная вода, выделяющаяся в виде капель, не допускается. Подача смазочного материала к узлам электрокаров и автопогрузчиков производится заливкой масла из масленки, например, в картер дифференциала, или с помощью шприцев в пресс-масленки.

Пресс-масленки состоят из стального шарика и пружины, вставленных в корпус. Поступающая в масленку смазка отжимает шарик и проходит к смазываемому узлу. При прекращении подачи смазки пружина выталкивает шарик, и он закрывает отверстие в масленке.

Пресс-масленки могут быть запрессованы в корпус детали машины (рис. 76, а) или ввинчены (рис. 76, б и в). Консистентная смазка нагнетается в пресс-масленку ручным шприцем, наконечник которого своими планками (рис. 77) плотно охватывает шаровую или коническую головку масленки.

Шприцы выпускаются двух типов — с рабочим объемом 200 см3 с передачей усилия руки через рукоятку (рис. 77, а) и на 120 см3 с передачей усилия через корпус (рис. 77, б). Шприцы обеспечивают давление до 250 кГ/см2 и подачу не менее 0,35 г смазки за каждый полный ход плунжера. При нажатии на рукоятку или корпус трубка входит в нижнюю часть корпуса, а находящаяся в ней смазка плунжером выдавливается в масленку.

По окончании заправки пружина разжимается и возвращает трубку в исходное положение. Новая порция смазки поступает в полость трубки через отверстия при очередном нажатии на рукоятку или корпус шприца.

Рекламные предложения:

Читать далее: Эксплуатация и ремонт электрооборудования электрокаров

Категория: — Электрокары

Главная → Справочник → Статьи → Форум

Что такое вязкость? Почему это важно для описания жидкостей?

Вязкость определяется как сопротивление потоку!

Вязкость часто называют толщиной жидкости. Вы можете представить себе воду (низкая вязкость) и мед (высокая вязкость). Однако это определение может сбивать с толку, когда мы смотрим на жидкости с разной плотностью.

На молекулярном уровне вязкость — это результат взаимодействия между различными молекулами жидкости.Это также можно понимать как трение между молекулами жидкости. Как и в случае трения между движущимися твердыми телами, вязкость будет определять энергию, необходимую для движения жидкости.

Как это измерить?

Вязкость

можно измерить с помощью различных методов, от методов «сделай сам» до вискозиметров, доступных на рынке. (Посмотрите наш веб-семинар о различных типах вязкости!)

DIY Метод измерения вязкости:

Вы можете думать о разных жидкостях, которым нужно разное время, например, чтобы вылить их из чашки.Вода выльется из стакана за доли секунды и за столь же короткое время примет форму принимающей емкости. С другой стороны, жидкости с высокой вязкостью, такой как мед, потребуется несколько минут, чтобы вылиться, а поверхность раздела между медом и воздухом займет столько же времени, чтобы осесть. Вы могли заметить, что я говорил о времени, пытаясь установить, какая из этих двух жидкостей более вязкая. Это то, что мы называем измерением кинематической вязкости или скорости потока жидкости при заданной силе, приложенной к ней.В этом примере приложенная сила — это сила тяжести. (Говоря о еде, что находится в меню вязкости? Узнайте больше о вязкости пищи!)

Вернемся к теме, еще один способ подумать об этом — использовать поршневую или шприцевую установку. Представьте, что внутри шприца находится жидкость (вода) очень низкой вязкости. Вероятно, вы сможете вытолкнуть жидкость пальцами. С другой стороны, если у вас внутри шприца мед, вам лучше иметь довольно прочный шприц и какую-нибудь механическую систему, которая поможет вам приложить достаточное усилие.Вы также могли заметить, что в этом случае я прилагаю и измеряю силу, чтобы жидкость текла. Если я фиксирую время, которое я хочу использовать для впрыска (или скорость нагнетания), и измеряю силу или напряжение, это то, что мы будем называть измерением динамической вязкости.

Количество методов и типов вискозиметров, используемых для измерения вязкости, довольно велико, и история вискозиметрии восходит к давней истории. В целом мы можем сузить круг вариантов, проанализировав их базовые принципы.Описанные выше измерения вязкости часто разделяют на кинематическую или динамическую. В то время как относительная вязкость может дать вам общее число, инструменты, которые могут измерять динамическую вязкость или абсолютную вязкость, были усовершенствованы и доказали, что они обеспечивают более надежные и точные измерения. Это связано с тем, что вместо значений, сравнивающих жидкости друг с другом, дается абсолютная вязкость. Вискозиметры RheoSense, основанные на технологии VROC ^®, обеспечивают динамические или абсолютные измерения вязкости, которые являются абсолютно надежным инструментом для вашей работы!

Хотите получить дополнительную информацию о том, как вискозиметр может помочь в вашей работе?

Если вы хотите узнать больше о вязкости, ознакомьтесь с нашей серией НАЗАД К ОСНОВАМ о вязкости:

Точное измерение вязкости

, 1 апреля 2015 г.35, № 7)

Оценка возможности инъекций на критическом этапе деятельности по разработке биопроцессов

Фармацевтические компании все больше внимания уделяют разработке терапевтических препаратов с высокой концентрацией белка, которые позволяют пациентам лечить себя в домашних условиях путем самостоятельной инъекции. Однако составление терапевтических белков сопряжено со многими проблемами.

Составы с высокими концентрациями белка имеют проблемы с присущей вязкостью. Такой состав требует высоких усилий впрыска, которые затрудняют инъекцию.Терапевтически многообещающий лекарственный препарат-кандидат может быть отклонен из-за высокой вязкости или потребовать разработки альтернативного метода доставки.

Кроме того, основные усилия направлены на элегантный молекулярный синтез кандидатов в лекарственные средства с высокой эффективностью, и известно, что незначительные изменения в структуре также могут оказывать заметное влияние на вязкость.

Например, вариации в небольших, но важных областях, определяющих комплементарность (CDR) терапевтических антител, могут влиять на вязкость составов антител, вызывая поразительные зависящие от концентрации эффекты на вязкость. Рисунок 1 ясно показывает, что поведение вязкости моноклональных антител (mAb) с небольшими вариациями может резко отличаться в зависимости от концентрации.

Если вязкость терапевтического белка-кандидата превышает 30-50 мПа · с (сП) при его дозовой концентрации, чаще всего он будет исключен из процесса разработки. Следовательно, очень важно измерять вязкость на ранних стадиях разработки лекарств. Но это создает дополнительную проблему.

На этих ранних стадиях обычно доступны лишь небольшие количества лекарств-кандидатов; поэтому приборы для измерения вязкости должны точно измерять небольшие объемы пробы. RheoSense производит вискозиметр с прямоугольной щелью, VROC ^® (вискозиметр / реометр на кристалле), который измеряет вязкость по перепаду давления испытательной жидкости, протекающей через стеклянную прямоугольную щель с контролируемой скоростью сдвига.

Этот метод широко известен в науке, а технология VROC теперь является общественным стандартом в США.S. Pharmacopeia. Преимущество конструкции VROC заключается в том, что она может точно измерять образцы размером до 50 микролитров.

Рис. 1. Вязкость mAb-h быстро увеличивается с повышением концентрации, и mAb-h, таким образом, будет наименее подходящим кандидатом в качестве инъекционного препарата. (Изменено из Yadav et al., 2010, J Pharm Sci 99: 4812-29.)

Интерфейс воздух / раствор

Хотя вязкость белковых растворов измеряли с помощью различных вискозиметров или реометров, другая проблема, присущая точным измерениям вязкости белковых растворов, недавно прояснилась в серии научных отчетов.

Подробные эксперименты показали, что традиционные вискозиметры и реометры, для которых требуется граница раздела воздух / раствор, дают ошибочные измерения высокой вязкости. Белки представляют собой амфифильные молекулы, которые в водных растворах имеют тенденцию перемещаться к границе раздела воздух / жидкость, чтобы минимизировать потенциальную энергию, как показано на Рис. 2A . Накопленные молекулы белка на границе раздела образуют вязкоупругую пленку, которая влияет на кажущуюся вязкость раствора.

Рисунок 2B показывает, что вязкость, измеренная с помощью конического и пластинчатого реометра (схема показана на Рисунок 2A ), ошибочно дает результаты измерений высокой вязкости образцов, подвергнутых низкой скорости сдвига, потому что он оценивает межфазный слой белка, а не сам раствор белка. .Кроме того, значения вязкости, определенные при низких скоростях сдвига, ошибочно оказываются зависимыми от скорости сдвига.

Однако есть несколько вискозиметров, которые не имеют границы раздела воздух / жидкость, в том числе стеклянные капиллярные вискозиметры и щелевые вискозиметры. Рисунок 2B также показывает вязкость тех же образцов, измеренную с помощью щелевого вискозиметра m -VROC с замкнутой системой (схематически показано на Рисунок 2C ).

Рис. 2. (A) Схема конического и пластинчатого реометра с раствором белка, подвергающимся воздействию воздуха, и молекулы белка, накапливающиеся на границе раздела воздух / жидкость.(B) Различные концентрации белковых растворов, измеренные с помощью конического и пластинчатого реометра, показывают ошибочно высокие значения вязкости (? [Па · с]), которые зависят от скорости сдвига ([с-1]) при низких скоростях сдвига, тогда как измеренные те же концентрации с вискозиметром VROC показывает вязкость, не зависящую от скорости сдвига. (C) Схема проточного канала щелевого вискозиметра, показывающая, что образец не подвергается воздействию воздуха, где Q — скорость потока, а P1 и P2 — местные давления, измеренные соответствующими датчиками давления.(2A и 2B модифицированы из Sharma et al., 2011, Soft Matter 7, 5150-5160.)

Скорость сдвига

До сих пор мы описали проблемы измерения вязкости белков, которые являются кандидатами для инъекционных составов. Однако наиболее важной переменной для точной оценки возможности инъекции является вязкость раствора белка, измеренная при скорости сдвига внутри иглы во время инъекции.

Скорость сдвига (_a) и падение давления (DP) внутри иглы и цилиндра шприца можно точно оценить, используя соответственно формулу.1 и уравнение Хагена-Пуазейля (уравнение 2), где Q — скорость нагнетания, R — радиус, l — длина и η — вязкость. Уравнение Хагена-Пуазейля описывает поток через круглые трубки, такие как игла и цилиндр шприца, как показано на рис. 3 .

Рис. 3. Схема предварительно заполненного шприца. F — сила, необходимая для толкания поршня; Fv — сила сопротивления, вызванная давлением P1, действующим на поршень.

Сила впрыска (F) равна силе давления, приложенной к поршню (Fv), и силе трения между цилиндром и поршнем.Давление, вызванное внутренним сопротивлением жидкости потоку, которое представляет собой вязкость, представляет собой совокупную сумму падений давления в цилиндре вдоль зоны сжатия от цилиндра к игле и игле.

Отношение падения давления в игле к перепаду давления в цилиндре оценивается по формуле. 2 составляет 300 000 к 1 для типичного предварительно заполненного шприца из-за заметных различий между радиусом иглы и радиусом цилиндра. Высокое соотношение предполагает, что падение давления в игле является основным фактором сопротивления нагнетанию высоковязкой жидкости.Таким образом, очень важно оценить динамику потока в игле.

Чтобы понять динамику в игле, скорость сдвига в игле для типичных скоростей закачки должна быть оценена с помощью уравнения. 1. Для игл 26 и 27 калибра со скоростью впрыска от 0,06 мл / с до 0,2 мл / с скорость сдвига находится в диапазоне от 50 000 с ^-1 до 200 000 с ^-1. Для точной оценки падения давления очень важно измерить вязкость раствора при скорости сдвига в игле, поскольку вязкость при низких скоростях сдвига может не иметь значения.

Хотя многие белковые растворы демонстрируют ньютоновское поведение, недавние исследования показали, что могут быть неньютоновские концентрированные белковые растворы с вязкостью, зависящей от скорости сдвига. Эти составы будут иметь вязкость при высоких скоростях сдвига, которые отличаются от их вязкости при низких скоростях сдвига, доступных для большинства вискозиметров.

Вискозиметр m -VROC, однако, позволяет измерять вязкость при высоких скоростях сдвига, не вызывая нестабильности потока, с которой сталкиваются другие приборы, поскольку небольшая глубина канала потока обеспечивает стабильный и ламинарный поток.Вязкость неньютоновского состава, которая может уменьшаться при высоких скоростях сдвига, превышающих 1000000 с. ^-1, может быть измерена с помощью вискозиметра м -VROC. После измерения вязкости при скорости сдвига в игле усилие впрыска можно оценить с помощью следующего уравнения:

(где b обозначает цилиндр, а n обозначает иглу. Для большинства инъекций с использованием маленькой иглы вклад трения поршня незначителен.)

Терапевтические белковые составы, которые являются кандидатами для инъекционных препаратов, имеют повышенную вязкость, что затрудняет инъекцию. Только небольшие образцы могут быть доступны для оценки на ранних этапах разработки. Белки-кандидаты могут проявлять неньютоновское поведение и образовывать вязкоупругие пленки на границах раздела жидкость / воздух. Щелевой вискозиметр м -VROC с замкнутой системой может учитывать эти проблемные особенности и обеспечивать измерения вязкости при высоких скоростях сдвига в игле.

Сонги Пэк, Ph.Д. ([email protected]), президент и генеральный директор RheoSense.

Шприцевые насосы «сделай сам» по сравнению с коммерческими шприцевыми насосами

Сравнение шприцевых насосов «сделай сам»

В этом кратком обзоре мы проанализируем возможность создания вашего шприцевого насоса, используя методы «сделай сам», доступные в литературе. Также мы рассмотрим факты и возможности этих устройств; мы покажем плюсы и минусы их изготовления. Наконец, профессиональные шприцевые насосы отличаются надежностью, и в следующих разделах будут представлены функции, которые делают их наилучшим вариантом.

Что такое шприцевой насос своими руками?

Изготовление самодельного шприцевого насоса — это самодельное лабораторное устройство, которое позволяет перемещать шприц через микрошаговый двигатель и контроллер с платами Arduino или Raspberry. Разработать собственное — непростая задача, потому что это сложное электромеханическое устройство. Однако можно создать и изготовить шприцевой насос с помощью технологии 3D-печати. Кроме того, контроллеры (Arduino и Raspberry) работают через интерфейсы Python.Удерживающие устройства могут стоить всего 5% от стоимости коммерческого шприцевого насоса. Тем не менее, время и практика проб и ошибок имеют решающее значение для получения воспроизводимого устройства. Кроме того, будущее микрофлюидики потребует опыта пользователя.

Сделай сам по сравнению с коммерческим шприцевым насосом

Принимая во внимание один из лучших шприцевых насосов «сделай сам», о котором сообщалось, — Nema 17, цена вполне доступна — 100 долларов США. Однако скорость потока в шприце этого типа составляет 2 штуки.1 мл / и линейное усилие как 200 Н с точностью 5%, воспроизводимостью 2,1% — лучшие результаты, полученные с помощью этого недорогого шприцевого насоса. Если мы сравним эти характеристики со шприцевым насосом Chemyx Fusion Touch 4000, мы обнаружим, что с точностью 0,35% и воспроизводимостью 0,05% шприцевые насосы Chemyx в 10 раз точнее и в 40 раз воспроизводимостью ². Кроме того, разрешение шага составляет 16 нанометров. Если пользователь хочет добиться микрожидкостного контроля с помощью устройства DIY, цена может вырасти до 720 евро за счет внедрения системы контроля давления ¹ ⁠.

Выводы

Заманчиво сэкономить на устройствах DIY, и для небольших приложений с более низкими требованиями это может быть хорошей идеей. Тем не менее, Chemyx предлагает лучшие шприцевые насосы, оптимизированные для своих ценных клиентов, благодаря возможности обеспечивать наиболее надежный и контролируемый поток независимо от вязкости или более низкой скорости потока. Такие применения не могут быть достигнуты с помощью шприцевых насосов DIY, в этом отношении, если пользователь хочет работать с новыми разработками, вышеупомянутые шприцевые насосы Chemyx являются лучшим выбором по сравнению с неоптимизированными шприцевыми насосами DIY.

Ссылки

Frank, P., Haefner, S., Elstner, M., Richter, A., 2016. Полностью программируемый, недорогой, самостоятельный источник давления для общего использования в микрофлюидная лаборатория. Inventions 1, 13. https://doi.org/10.3390/inventions1020013
Wijnen, B., Hunt, E.J., Anzalone, G.C., Pearce, J.M., 2014. Библиотека шприцевых насосов с открытым исходным кодом. PLoS One 9, 1–8. https://doi.org/10.1371/journal.pone.0107216

Почему я не могу получить надежные измерения вязкости моей тиксотропной жидкости с помощью чашки Zahn? — Часть III

В части II этой серии мы продолжили обсуждение вязкости, затронув тему тиксотропии.Определив это, мы можем вернуться, чтобы собрать все воедино и показать, как разные методы измерения дают разные результаты и как наш выбор измерения может на самом деле работать против нас.

Процесс измерения чашки

Основной процесс измерения чашек прост. Чашка полностью погружена в жидкость и вытягивается прямо вверх и наружу. Время, необходимое для стекания жидкости из чашки, определяет вязкость в «чашке-секундах».

Выглядит достаточно просто, правда? Но, как мы отмечали в Части I этой серии статей, с этим простым процессом связано множество проблем.

Когда мне начать отсчет времени? Когда верхняя часть чашки разбивает поверхность? Когда дно чашки очищает поверхность?

А когда мне остановиться? Когда поток впервые прерывается? Когда он рассыпается на капельки? Когда чашка пуста?

И, если стакан не поднимается прямо вверх, это влияет на поток через отверстие, перенаправляя давление на отверстие к стенке стакана.Итак, насколько прям прям?

Это восток, чтобы понять, почему разные операторы получают разные показания.

Итак, давайте посмотрим, что на самом деле происходит за кулисами…

Физика за измерениями чашки

Когда чаша вынимается из жидкости, она наполняется. Объем жидкости в чашке оказывает давление на жидкость в отверстии под действием силы тяжести. Учитывая наше обсуждение в Части I этой серии, это основное определение кинематической вязкости.Существует также вес атмосферы, давящей на поверхность жидкости, но он постоянен для любого данного места (в основном из-за высоты) и разнообразия чашек (объем, диаметр, размер отверстия и т. Д.), Поэтому мы можем игнорировать это в нашем обсуждении.

Когда сила тяжести тянет жидкость вниз, она «выталкивается» через отверстие. В результате в жидкость вносится некоторый сдвиг. Но эта «сила» определяется объемом в чашке — и он уменьшается со временем, а это означает, что сила, действующая на жидкость, проходящую через отверстие, также уменьшается с течением времени.В результате сдвиг в жидкости также уменьшается.

Следующий действительно важный вопрос: «Достаточно ли силы / сдвига для полного истончения материала при сдвиге?» Ссылаясь на Рисунок 2 в Части II этой серии, это означает, что мы переместим его через Первый Ньютоновский диапазон, через переходный диапазон (в середине) и во Второй Ньютоновский диапазон, достаточно далеко, чтобы достичь стабильной вязкости. Если вы думаете об объеме жидкости в чашке, размере отверстия, времени, необходимом для прохождения жидкости через это отверстие, и думаете, что маловероятно, что мы выйдем из этого Первого Ньютоновского диапазона, не говоря уже о том, чтобы добраться до Второго Ньютоновского хребта, вы до сих пор довольно хорошо понимаете нашу дискуссию!

Итак, что, если сдвиг действительно пройдет через Первый Ньютоновский диапазон, только чтобы упасть где-то в середине переходного диапазона? Если вы сказали, что результаты измерений будут нестабильными и ненадежными из-за взаимодействия между сдвигом и вязкостью, вы будете правы.И это еще одна причина того, что результаты измерения чашек различаются — абсолютно не по вине оператора.

Почему измерения на моем стакане не совпадают с моим автоматическим вискозиметром

Это общий вопрос, который задают практически всем производителям вискозиметров (нет, мы не одиноки — и да, мы говорим!) Но после этого обсуждения, вероятно, будет легче понять, что автоматические вискозиметры измеряют вязкость, измеряя необходимое усилие. чтобы ввести в жидкость сдвиг — во многом так же, как Ньютон изначально определил вязкость.Механическому вискозиметру намного легче ввести сдвиг в жидкость, чем гравитационному.

Еще один интересный факт заключается в том, что большинство вискозиметров калибруются с помощью ньютоновских жидкостей — калибровочных стандартов, разработанных так, чтобы их характеристики (читай: вязкость) были очень последовательными и предсказуемыми по своим характеристикам (читай: вязкости) как при сдвиге, так и при температуре. Если вы измеряете ньютоновскую жидкость и механическим вискозиметром, и чашкой, измерения будут очень близкими, потому что сдвиг не играет роли. Но неньютоновские жидкости — это совсем другая история.

Когда измерение вязкости бесполезно?

Учитывая известное влияние вязкости на результаты наших процессов дозирования жидкости, это может показаться глупым вопросом. Но с практической точки зрения многие измерения вязкости, которые мы проводим, бесполезны.

Итак, когда — это , измерение вязкости бесполезно?

Когда вязкость жидкости измеряется в условиях, которые не совпадают или даже отдаленно похожи на те, с которыми жидкость будет сталкиваться в нашем процессе! И учитывая наше обсуждение ньютоновских и неньютоновских жидкостей и влияния сдвига — как на наши измерения, так и на результаты нашего процесса, довольно легко сделать вывод, что измерение в чашке редко воспроизводит современные условия процесса.

Тогда почему измерения в чашках?

К настоящему времени вы, вероятно, вернулись к тому, с чего мы начали, и спрашиваете себя: «Если все это правда, почему все зависит от измерения чашек для управления своим процессом?»

И это справедливый вопрос.

Измерения в чашках используются уже давно — намного дольше, чем для сложных жидкостей, которые большинство из нас сегодня использует в своих процессах. И по сравнению со сложными измерительными системами чашки дешевы.А на снятие показаний в чашке уходит не больше минуты или двух, поэтому измерения обходятся дешево.

Это подводит нас к вековому правилу: «Вы получаете то, за что платите!»

Дело в том, что нам нужно определить измерение, которое точно предсказывает, как наша жидкость будет работать в нашем процессе . Реализуй это. И придерживайтесь этого.

¹ — Графики любезно предоставлены Sofraser

Кинематический вискозиметр: SVM :: Anton-Paar.com

D341 2001, 3001, 4001

D396 2001, 3001, 4001

D975 2001, 3001, 4001

D1250 3001, 4001

D1655 3001

D2161 2001, 3001, 4001

D2270 3001, 4001

D2501 3001, 4001

D2502 2001, 3001, 4001

D2603 2001, 3001, 3001 Холодные свойства, 4001

D2880 2001, 3001, 4001

D3238 3001

D3238 4001

D3699 2001, 3001, 3001 Холодные свойства, 4001

D4052 3001, 4001

D4054 3001

D4174 2001, 3001, 4001

D4378 2001, 3001, 3001 Холодные свойства, 4001

D5002 3001, 4001

D5275 2001, 3001, 3001 Холодные свойства, 4001

D5372 2001, 3001, 4001

D5621 2001, 3001, 3001 Холодные свойства, 4001

D6074 2001, 3001, 4001

D6080 2001, 3001, 3001 Холодные свойства, 4001

D6158 2001, 3001, 3001 Холодные свойства, 4001

D6278 2001, 3001, 3001 Холодные свойства, 4001

D6287 2001, 3001, 3001 Холодные свойства, 4001

D6448 2001, 3001, 4001

D6666 2001, 3001, 3001 Холодные свойства, 4001

D6710 2001, 3001, 4001

D6751 2001, 3001, 3001 Холодные свойства, 4001

D6823 2001, 3001, 4001

D7042 2001, 3001, 4001

D7109 2001, 3001, 3001 Холодные свойства, 4001

D7152 2001, 3001, 4001

D7155 2001, 3001, 4001

D7223 3001

D7467 2001, 3001, 3001 Холодные свойства, 4001

D7566 3001

D7665 2001, 3001, 4001

D7666 2001, 3001, 4001

D7720 2001, 3001, 4001

D7752 2001, 3001, 4001

D7826 3001

D7863 2001, 3001, 4001

D7973 2001, 3001, 3001 Холодные свойства, 4001

D8029 2001, 3001, 3001 Холодные свойства, 4001

D8046 2001, 3001, 4001

D8128 2001, 3001, 4001

D8147 3001

D8181 2001, 3001, 4001

D8185 2001, 3001, 4001

F3208 2001, 3001, 4001

F3337 2001, 3001, 4001

12.4: вязкость и ламинарный поток; Закон Пуазейля

Цели обучения

К концу этого раздела вы сможете:

Определите ламинарный поток и турбулентный поток.
Объясните, что такое вязкость.
Рассчитайте расход и сопротивление по закону Пуазейля.
Объясните, как давление падает из-за сопротивления.

Ламинарный поток и вязкость

Когда вы наливаете себе стакан сока, жидкость течет свободно и быстро.Но когда вы поливаете блины сиропом, эта жидкость медленно течет и прилипает к кувшину. Разница заключается в трении жидкости как внутри самой жидкости, так и между жидкостью и окружающей средой. Мы называем это свойство жидкости вязкостью . Сок имеет низкую вязкость, тогда как сироп имеет высокую вязкость. В предыдущих разделах мы рассматривали идеальные жидкости с небольшой вязкостью или без нее. В этом разделе мы исследуем, какие факторы, включая вязкость, влияют на скорость потока жидкости.

Точное определение вязкости основано на ламинарном или нетурбулентном потоке. Прежде чем мы сможем определить вязкость, нам нужно определить ламинарный поток и турбулентный поток. На рисунке показаны оба типа потока. Ламинарный поток характеризуется плавным течением жидкости слоями, которые не смешиваются. Турбулентный поток или турбулентность характеризуется вихрями и завихрениями, которые смешивают слои жидкости вместе.

Рисунок \ (\ PageIndex {1} \): Дым плавно поднимается на некоторое время, а затем начинает образовывать завихрения и вихри.Плавный поток называется ламинарным потоком, тогда как завихрения и водовороты типичны для турбулентного потока. Если вы посмотрите на дым (стараясь не дышать на него), вы заметите, что при плавном течении он поднимается быстрее, чем после того, как он становится турбулентным, что означает, что турбулентность оказывает большее сопротивление потоку. (кредит: Creativity103)

На рисунке схематически показано, чем отличаются ламинарный и турбулентный потоки. Слои текут без перемешивания, когда поток ламинарный. Когда есть турбулентность, слои перемешиваются, и есть значительные скорости в направлениях, отличных от общего направления потока.Линии, показанные на многих иллюстрациях, представляют собой пути, по которым проходят небольшие объемы жидкости. Они называются линиями обтекания . Линии тока плавные и непрерывные, когда поток является ламинарным, но разделяются и перемешиваются, когда поток является турбулентным. У турбулентности есть две основные причины. Во-первых, любое препятствие или острый угол, например в кране, создает турбулентность, сообщая скорости, перпендикулярные потоку. Во-вторых, высокие скорости вызывают турбулентность. Сопротивление как между соседними слоями жидкости, так и между жидкостью и окружающей средой образует завихрения и водовороты, если скорость достаточно велика.В оставшейся части этого раздела мы сконцентрируемся на ламинарном потоке, оставив некоторые аспекты турбулентности для последующих разделов.

Рисунок \ (\ PageIndex {2} \): (a) Ламинарное течение происходит слоями без перемешивания. Обратите внимание, что вязкость вызывает сопротивление между слоями, а также с неподвижной поверхностью. (b) Препятствие в судне вызывает турбулентность. Турбулентный поток перемешивает жидкость. Здесь больше взаимодействия, больше нагрева и больше сопротивления, чем в ламинарном потоке.

Установление связей: эксперимент на вынос: спуститься к реке

Попробуйте одновременно бросить две палки в текущую реку: одну у края реки, а другую — у середины.Какой из них путешествует быстрее? Почему?

На рисунке показано, как измеряется вязкость жидкости. Между двумя параллельными пластинами находится определенная жидкость. Нижняя пластина фиксируется, а верхняя пластина перемещается вправо, увлекая за собой жидкость. Слой (или пластинка) жидкости, контактирующий с любой пластиной, не перемещается относительно пластины, поэтому верхний слой перемещается, в то время как нижний слой остается в покое. Каждый последующий слой сверху вниз оказывает силу на слой под ним, пытаясь утащить его, создавая непрерывное изменение скорости от до 0, как показано.Необходимо следить за тем, чтобы поток был ламинарным; то есть слои не смешиваются. Движение на рисунке похоже на непрерывное режущее движение. Жидкости имеют нулевую прочность на сдвиг, но скорость , с которой они сдвигаются, связана с теми же геометрическими факторами \ (A \) и \ (L \), что и деформация сдвига для твердых тел.

Рисунок \ (\ PageIndex {3} \): График показывает ламинарный поток жидкости между двумя пластинами области \ (A \). Нижняя пластина закреплена. Когда верхняя пластина сдвигается вправо, она увлекает за собой жидкость.

Сила \ (F \) требуется, чтобы верхняя пластина на рисунке двигалась с постоянной скоростью \ (v \), и эксперименты показали, что эта сила зависит от четырех факторов. Во-первых, \ (F \) прямо пропорционально \ (v \) (до тех пор, пока скорость не станет настолько высокой, что возникает турбулентность — тогда требуется гораздо большая сила, и она имеет более сложную зависимость от \ (v \)). Во-вторых, \ (F \) пропорционален площади \ (A \) пластины. Это соотношение кажется разумным, поскольку \ (A \) прямо пропорционально количеству перемещаемой жидкости.В-третьих, \ (F \) обратно пропорционально расстоянию между пластинами \ (L \). Это соотношение также разумно, \ (L \) подобен плечу рычага, и чем больше плечо рычага, тем меньше силы требуется. В-четвертых, \ (F \) прямо пропорционален коэффициенту вязкости , \ (\ eta \). Чем больше вязкость, тем больше требуется сила. Эти зависимости объединены в уравнение

\ [F = \ eta \ dfrac {\ nu A} {L}, \]

, который дает нам рабочее определение вязкости жидкости \ (\ eta \).2) s \, или \, Pa \ cdot s \), в таблице приведены коэффициенты вязкости для различных жидкостей.

Вязкость варьируется от одной жидкости к другой на несколько порядков. Как и следовало ожидать, вязкость газов намного меньше вязкости жидкостей, и эта вязкость часто зависит от температуры. Вязкость крови можно уменьшить, употребляя аспирин, что позволяет ему легче циркулировать по телу. (При длительном применении в низких дозах аспирин может помочь предотвратить сердечные приступы и снизить риск свертывания крови.)

Ламинарный поток, ограниченный трубками — закон Пуазейля

Что вызывает поток? Ответ, что неудивительно, — разница в давлении. Фактически, существует очень простая взаимосвязь между горизонтальным потоком и давлением. Расход \ (Q \) находится в направлении от высокого давления к низкому. Чем больше перепад давления между двумя точками, тем больше расход. Это отношение может быть указано как

\ [Q = \ dfrac {P_2 — P_1} {R}, \]

, где \ (P_1 \) и \ (P_2 \) — давление в двух точках, например, на любом конце трубы, а \ (R \) — сопротивление потоку.Сопротивление \ (R \) включает все, кроме давления, которое влияет на скорость потока. Например, для длинной трубки \ (R \) больше, чем для короткой. Чем больше вязкость жидкости, тем больше значение \ (R \). Турбулентность сильно увеличивает \ (R \), тогда как увеличение диаметра трубы уменьшает \ (R \).

Если вязкость равна нулю, жидкость не имеет трения и сопротивление потоку также равно нулю. Сравнивая поток без трения в трубе с вязким потоком, как показано на рисунке, мы видим, что для вязкой жидкости скорость максимальна в середине потока из-за сопротивления на границах.4}. \]

Это уравнение называется законом Пуазейля для сопротивления в честь французского ученого Ж. Л. Пуазейля (1799–1869), который вывел его в попытке понять течение крови, часто турбулентной жидкости.

Рисунок \ (\ PageIndex {4} \): (a) Если поток жидкости в трубке имеет незначительное сопротивление, скорость по всей трубке одинакова. (b) Когда вязкая жидкость течет через трубку, ее скорость на стенках равна нулю, постоянно возрастая до максимума в центре трубки. (c) Форма пламени горелки Бунзена обусловлена профилем скорости в трубе.(кредит: Джейсон Вудхед)

Давайте исследуем выражение Пуазейля для \ (R \), чтобы увидеть, имеет ли оно хороший интуитивный смысл. Мы видим, что сопротивление прямо пропорционально вязкости жидкости \ (\ eta \) и длине \ (l \) трубки. 4} {8 \ eta l}.{0,25} r_1 \) уменьшение радиуса артерии на 16%.

Обсуждение

Это уменьшение радиуса на удивление мало для данной ситуации. Для восстановления кровотока, несмотря на это увеличение, потребуется увеличение разницы давлений \ ((P_2 — P_1) \) в два раза с последующей нагрузкой на сердце.

\ (\ PageIndex {1} \)
Жидкость	Температура (ºC)	Вязкость (мПа⋅с)
*Газы*
Воздух	0	0.0171
	20	0,0181
	40	0,0190
	100	0,0218
Аммиак	20	0,00974
Двуокись углерода	20	0.0147
Гелий	20	0,0196
Водород	0	0,0090
Меркурий	20	0,0450
Кислород	20	0,0203
Пар	100	0.0130
*Жидкости*
Вода	0	1,792
	20	1,002
	37	0,6947
	40	0.653
	100	0,282
Цельная кровь ¹	20	3,015
	37	2,084
Плазма крови ²	20	1,810
	37	1.257
Этиловый спирт	20	1,20
Метанол	20	0,584
Масло (тяжелая машина)	20	660
Масло (моторное, SAE 10)	30	200
Масло (оливковое)	20	138
Глицерин	20	1500
Мед	20	2000–10000
Кленовый сироп	20	2000–3000
Молоко	20	3.0
Масло (кукуруза)	20	65

Система кровообращения дает множество примеров действующего закона Пуазейля — кровоток регулируется изменениями размера сосудов и кровяного давления. Кровеносные сосуды не жесткие, а эластичные. Регулировка кровотока в основном осуществляется путем изменения размера сосудов, поскольку сопротивление очень чувствительно к радиусу. Во время интенсивных упражнений кровеносные сосуды выборочно расширяются до важных мышц и органов, и повышается кровяное давление.4 = 0,81 \) от первоначального значения. Уменьшение расхода на 19% вызвано уменьшением радиуса на 5%. Организм может компенсировать это повышением кровяного давления на 19%, но это представляет опасность для сердца и любых сосудов с ослабленными стенками. Другой пример — автомобильное моторное масло. Если у вас есть автомобиль с манометром масла, вы можете заметить, что давление масла высокое, когда двигатель холодный. Вязкость моторного масла в холодном состоянии выше, чем в теплом, поэтому давление должно быть выше, чтобы перекачивать такое же количество холодного масла.2 \]

Обсуждение

Это давление может быть обеспечено с помощью баллона для внутривенного вливания с поверхностью физиологического раствора на 1,61 м над входом в иглу (это оставлено вам для решения в Задачах и упражнениях этой главы), при условии, что перепад давления в игле пренебрежимо мал. трубка, ведущая к игле.

Поток и сопротивление как причины падений давления

Возможно, вы заметили, что давление воды в вашем доме может быть ниже обычного в жаркие летние дни, когда больше используется.Это падение давления происходит в водопроводе еще до того, как оно достигнет вашего дома. Давайте рассмотрим поток через водопровод, как показано на рисунке \ (\ PageIndex {6} \). Мы можем понять, почему давление \ (P_1 \) в доме падает во время интенсивного использования, переставив

\ [Q = \ dfrac {P_2 — P_1} {R} \] до

\ [P_2 — P_1 = RQ, \]

, где в данном случае \ (P_2 \) — давление на водопроводной станции, а \ (R \) — сопротивление водопровода. Во время интенсивного использования расход \ (Q \) велик.Это означает, что \ (P_2 — P_1 = RQ \) справедливо как для ламинарных, так и для турбулентных течений.

Рисунок \ (\ PageIndex {6} \): во время интенсивного использования в водопроводе наблюдается значительный перепад давления, и \ (P_1 \), подаваемый пользователям, значительно меньше, чем \ (P_2 \), создаваемый в воде. работает. Если расход очень мал, перепад давления незначителен, и \ (P_2 — P_1. \)

Мы можем использовать \ (P_2 — P_1 = RQ \) для анализа перепадов давления, возникающих в более сложных системах, в которых радиус трубы не везде одинаково.Сопротивление будет намного выше в узких местах, таких как закупорка коронарной артерии. Для данного расхода \ (Q \) перепад давления будет наибольшим там, где труба наиболее узкая. Так водопроводные краны управляют потоком. Кроме того, \ (R \) значительно увеличивается из-за турбулентности, а сужение, которое создает турбулентность, значительно снижает давление ниже по потоку. Зубной налет в артерии снижает давление и, следовательно, поток, как за счет сопротивления, так и за счет создаваемой турбулентности.

Рисунок \ (\ PageIndex {7} \) представляет собой схему кровеносной системы человека, показывающую среднее артериальное давление в ее основных частях для взрослого человека в состоянии покоя.Давление, создаваемое двумя насосами сердца, правым и левым желудочками, снижается за счет сопротивления кровеносных сосудов, когда кровь течет через них. Левый желудочек увеличивает артериальное давление, что приводит к току крови через все части тела, кроме легких. Правый желудочек получает кровь с более низким давлением из двух основных вен и перекачивает ее через легкие для газообмена с атмосферными газами — удаления углекислого газа из крови и пополнения запасов кислорода.Схематически показан только один крупный орган с типичным разветвлением артерий на все более мелкие сосуды, самые маленькие из которых — капилляры, и воссоединение мелких вен с более крупными. Подобное разветвление происходит во множестве органов тела, и система кровообращения обладает значительной гибкостью в регулировании потока к этим органам за счет расширения и сужения артерий, ведущих к ним, и капилляров внутри них. Чувствительность потока к радиусу трубки делает эту гибкость возможной в большом диапазоне скоростей потока.

Рисунок \ (\ PageIndex {7} \): Схема кровеносной системы. Перепад давления создается двумя насосами в сердце и уменьшается за счет сопротивления сосудов. Разветвление сосудов в капилляры позволяет крови достигать отдельных клеток и обмениваться с ними веществами, такими как кислород и продукты жизнедеятельности. Система обладает впечатляющей способностью регулировать поток к отдельным органам, в основном за счет изменения диаметра сосудов.

Каждое разветвление более крупных сосудов на более мелкие увеличивает общую площадь поперечного сечения трубок, по которым течет кровь.2 \) Таким образом, сопротивление разветвлений уменьшается, так что давление полностью не теряется. Более того, поскольку \ (Q = A \ overline {v} \) и \ (A \) увеличивается из-за разветвления, средняя скорость крови в меньших сосудах уменьшается. Скорость крови в аорте \ ((диаметр = 1 \, см) \) составляет около 25 см / с, в то время как в капиллярах (\ (20 \, \ мкм \) в диаметре) скорость составляет около 1 мм / с. Эта пониженная скорость позволяет крови обмениваться веществами с клетками капилляров и, в частности, альвеол.4} {8 \ eta l}. \]

Падение давления, вызванное потоком и сопротивлением, определяется как \ [P_2 — P_1 = RQ. \]

Сноски

1 Отношения вязкости крови к воде почти постоянны между 0 ° C и 37 °

2. См. Примечание о цельной крови.

Глоссарий

ламинарный: Тип потока жидкости, в котором слои не смешиваются

турбулентность: Поток жидкости, в котором слои смешиваются вместе посредством завихрений и завихрений

вязкость: трение в жидкости, определяемое как трение между слоями

Закон Пуазейля для сопротивления: сопротивление ламинарному течению несжимаемой жидкости в трубке: R = 8 ηl / πr ⁴

Закон Пуазейля: скорость ламинарного течения несжимаемой жидкости в трубке: Q = ( P ₂ — P ₁) πr ⁴/8 ηl

Авторы и указание авторства

Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрикс (Государственный университет Нью-Йорка, колледж в Освего) с авторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет).Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

Смазка / силиконизация игл для уменьшения трения от инъекционных игл

Иглы для подкожных инъекций часто могут иметь высокое поверхностное трение из-за процесса их изготовления. Иглы имеют такую форму, чтобы свести к минимуму усилие, необходимое для прокалывания и проникновения в кожу (или другой субстрат). Однако трение о металлическую поверхность иглы может усложнить задачу.В результате требуется большее усилие как во время самого прокола (сила проникновения), так и при протаскивании иглы через кожу (сила сопротивления). Это может привести к большему повреждению кожи, чем необходимо, и меньшему комфорту для пациента.

Чтобы уменьшить трение между металлом иглы и кожей, можно использовать тонкий слой силикона для покрытия кончика иглы, добавляя смазку для иглы, которая значительно снижает трение.

Какой силикон используется для силиконизации?

Для этой цели можно использовать несколько типов силикона:

Силиконовая жидкость — это неотвержденный силикон PDMS, который может иметь разную вязкость (т.е.е. длина цепи силиконовых полимеров) и поэтому дают разные результаты.
Силиконовая жидкость также может быть диспергирована или эмульгирована в растворителе, чтобы сделать ее более управляемой. Это, например, случай использования силикона с очень высокой молекулярной массой. Обычно его вязкость слишком высока для работы.
Также можно использовать отверждающие силиконы. Эти типы силиконов часто являются аминофункциональными, и силиконовые полимеры в конечном итоге сшиваются, чтобы, как мы надеемся, создать более прочное покрытие, которое имеет более высокую адгезию к металлу.Также можно использовать силиконовый эластомер с низким коэффициентом трения.

Адгезия

Помимо максимального снижения трения при проникновении через кожу, также может иметь значение, чтобы силиконизация касалась его адгезии к игле для нескольких проникновений подряд. Например, игла для наложения швов должна оставаться комфортной в течение нескольких или многих стежков, в то время как другие типы игл предназначены только для одноразового использования. Даже с помощью обычной иглы, используемой для образцов крови или капельниц, может потребоваться несколько попыток найти вену.

В исследовании, проведенном Nusil ( Покрытие игл для уменьшения силы проникновения и сопротивления игл, 2012 ), силы игл с различными типами покрытий были испытаны для нескольких проколов иглой подряд. Исследование показало, что все виды силиконизации дают улучшение по сравнению с иглой без покрытия. Продукты, которые лучше всего сохраняли свой смазывающий эффект, представляли собой неотверждающуюся силиконовую дисперсию с очень высокой молекулярной массой. Считается, что причина его успеха связана с запутыванием длинных полимерных цепей вокруг кончика иглы в сочетании с межмолекулярными силами, действующими на металл.Эти свойства позволяют ему превзойти даже затвердевающие силиконы.

Медицинское разрешение на смазку игл

При выборе силикона для покрытия игл следует учитывать то обстоятельство, что силикон будет контактировать с пациентом и фактически будет имплантирован человеку на короткое время. Следовательно, для этой цели важно, чтобы силикон был одобрен с медицинской точки зрения. Сертификация ISO-10993 для краткосрочной имплантации является подходящим требованием.

продуктов Nusil к рассмотрению:

Лучшие результаты согласно исследованию: MED-4162

Отверждение: MED10-6670, MED-4159, MED10-4161

Неотверждаемая силиконовая жидкость: Nusil MED-361

Техника дозирования для смазки игл

Чаще всего силикон, используемый для силиконизации, разбавляют каким-либо растворителем для достижения вязкости, подходящей для погружения.Когда со временем растворитель испаряется, становится важным постоянно отслеживать вязкость и при необходимости добавлять больше. Это связано с тем, что вязкость напрямую влияет на толщину покрытия.

Более новый и сложный метод силиконизации игл заключается в использовании небольшого струйного клапана, основанного на пьезотехнологии, для нанесения на иглу желаемого количества силиконовой дисперсии.

Игла вставляется в камеру для нанесения покрытия, куда дозируется контролируемое количество силикона.В то же время импульс воздуха превращает его в туман. Таким образом, туман будет очень тонко покрывать иглу вокруг иглы. Избыток силиконового тумана будет удален из камеры.

Большим преимуществом этой системы является то, что силиконовая дисперсия полностью инкапсулируется перед ее переносом в камеру для нанесения покрытия. Это означает, что нет необходимости постоянно проверять вязкость и добавлять больше.

Еще одно интересное преимущество использования этого метода дозирования заключается в том, что струйная система может обрабатывать и более вязкие материалы.Это снижает количество растворителя, необходимого в процессе, что имеет как экологические, так и финансовые преимущества.

EFD Nordson, например, разработала дозирующую систему для этого типа применения:

Как определить вязкость краски по DIN своими руками: таблица значений

Вязкость лакокрасочных материалов

Что зависит от вязкости

Как измерить вязкость

Особенности измерения

Методы определения вязкости

Определение вязкости вискозиметром

«Народный метод» измерения вязкости («на глаз»)

В каких единицах измеряется

Оборудование для вязких материалов

Вязкость водоэмульсионной краски

Особенности определения вязкости краски для краскопульта

Какие значения считаются оптимальными

Видео: Как определить вязкость краски

виды дефектов при покраске автомобиля

Дефекты из-за несоблюдения требований указанных в инструкции

Готовим поверхность к покраске

Уральский следопыт | Уральский следопыт

1983 06 июнь

Учебная работа по физике «Вязкость жидкости»

Смазка и смазочные материалы электрокаров

Рекламные предложения на основе ваших интересов:

Рекламные предложения:

Главная → Справочник → Статьи → Форум

Что такое вязкость? Почему это важно для описания жидкостей?

Вязкость определяется как сопротивление потоку!

Как это измерить?

Точное измерение вязкости

Шприцевые насосы «сделай сам» по сравнению с коммерческими шприцевыми насосами

Сравнение шприцевых насосов «сделай сам»

Что такое шприцевой насос своими руками?

Сделай сам по сравнению с коммерческим шприцевым насосом

Выводы

Ссылки

Почему я не могу получить надежные измерения вязкости моей тиксотропной жидкости с помощью чашки Zahn? — Часть III

Кинематический вискозиметр: SVM :: Anton-Paar.com

12.4: вязкость и ламинарный поток; Закон Пуазейля

Ламинарный поток и вязкость

Ламинарный поток, ограниченный трубками — закон Пуазейля

Поток и сопротивление как причины падений давления

Сноски

Глоссарий

Авторы и указание авторства

Смазка / силиконизация игл для уменьшения трения от инъекционных игл

Какой силикон используется для силиконизации?

Адгезия

Медицинское разрешение на смазку игл

Техника дозирования для смазки игл

Добавить комментарий Отменить ответ