Как правильно объезжать препятствия на дороге? — Рамблер/авто
С каждым годом, ПДД вырастают всё в большее «яблоко раздора» между водителями и сотрудниками дорожной полиции. Многие пункты правил дорожного движения носят двоякий смысл, а другие и вовсе «не налезают на голову». Именно таким является правило объезда препятствия на дороге, ведь данная тема собирает вокруг себя огромное количество спорных ситуаций.
Что такое объезд препятствия?Как объезжать препятствия под предписывающие знаки?»Объезд препятствия справа»»Объезд препятствия слева»»Объезд препятствия справа или слева»Правила объездаМожно ли выезжать пересекать прерывистую для объезда?Разрешено ли пересекать сплошную?Пересечение двойной сплошной
Что такое объезд препятствия?
Прежде чем поговорит про объезд, необходимо определить, что такое препятствие на дороге и какое понятие даётся ему в ПДД. Итак, препятствие — это неподвижный объект, оказавшийся на полосе движения транспортных средств, который не даёт продвигаться далее по данной полосе. Под определение понятия «препятствие» не попадают заторы, а также другие транспортные средства, которое остановилось на полосе.
Под определение понятия «препятствие» не попадают заторы, а также другие транспортные средства, которое остановилось на полосе.
В то же время, «объездом» называют маневр, выполняемый водителем, с целью преодоления некоего препятствия, появившегося на пути движения транспортного средства. Тем не менее, в ПДД вы не найдёте чёткой дефиниции данного понятия. Давайте разъясним путаницу, часто возникающую в головах автомобилистов относительно того, что обгон и объезд – это разные понятия в ПДД. Если, например, на дороге проводятся ремонтные работы и она отчасти заблокирована, то проезд препятствия с одной из сторон относится к объезду. Но если впереди вас медленно едет большая фура, например, и вы её объезжаете, то это уже считается обгоном. Нельзя путать эти два понятия!
Важно! Неправильно совершённый обгон повлечёт за собой больший штраф, чем неправильный объезд.
Как объезжать препятствия под предписывающие знаки?
Пожалуй, утопия для водителей – это дорога, лишённая перекрёстков, пешеходных переходов, сужений и других препятствий для нормального и расслабленного движения в заданном направлении. Но в реальности, часто всё идёт не так, как хотелось бы. Ко всему прочему, на проезжей части могут образовываться и различные препятствия, а для регулировки движения на таких участках устанавливаются следующие предписывающие знаки.
Но в реальности, часто всё идёт не так, как хотелось бы. Ко всему прочему, на проезжей части могут образовываться и различные препятствия, а для регулировки движения на таких участках устанавливаются следующие предписывающие знаки.
Интересно! Двигаясь в условиях тумана, все встречаемые на пути объекты, кажутся водителю большими, чем они есть на самом деле.
«Объезд препятствия справа»
Дорожный знак 4.2.1 «Объезд препятствия справа» устанавливается с целью чёткого указания траектории, по которой следует объезжать объект, мешающий дальнейшему нормальному движению автомобиле. В данном случае, разрешается это делать только по правой стороне от него. Объезд слева недопустим. Знак действует только в зоне расположения упомянутого объекта, а после объезда препятствия, действия этого дорожного знака прекращается.
«Объезд препятствия слева»
Знак 4.2.2 требует объезжать препятствие только с левой стороны, несмотря на то, что его можно объехать и справа. По правилам дорожного движения, водитель обязан объезжать преграду только слева.
Часто, этот знак можно встретить на автомобилях коммунальных служб, дорожно-ремонтных организаций и других предприятий, проводящих дорожные ремонтные работы.
Случается и так, что знак 4.2.2 может противоречить требованиям сплошной горизонтальной линии разметки. В этой ситуации, водители должны помнить о приоритете и ориентироваться, в первую очередь. на то, куда указывает знак. Поэтому можно вполне законно пересекать разметку, чтобы объехать препятствие. Далее можно возвращаться на свою полосу.
Важно! Знак, как он есть, не даёт приоритета автомобилю, выполняющему объезд препятствия, поскольку преимущество имеет встречный транспорт.
«Объезд препятствия справа или слева»
«Объезд препятствия справа или слева» (знак 4.2.3) является наиболее популярным регулировочным средством на время проведения ремонтных работ посреди проезжей части и при необходимости объезда разного рода ограждений и конструкций.
Если выбирать траекторию движения логично, то водителю необходимо больше придерживаться правой стороны, чтобы не выезжать на встречную полосу. Если же выполнять манёвр влево, тогда нужно двигаться от неё на максимально возможном расстоянии.
Если же выполнять манёвр влево, тогда нужно двигаться от неё на максимально возможном расстоянии.
Это основы безопасности движения по полосам проезжей части. Однако водитель сам решает с какой стороны ему проще преодолеть преграду, но, в любом случае, безопасность должна быть превыше всего.
Знаете ли Вы? У индийских коров, имеющих статус священного животного, есть преимущество перед любым транспортным средством, зафиксированом в ПДД.
Правила объезда
Различные ситуации, связанные с объездом препятствий, являются очень проблемной правовой коллизией не только в Украине, но и в административных законодательствах других стран. Сотни водителей, только в столице, ежедневно встречают перед собой преграды в виде сломанного грузового автомобиля, машины с включенными аварийными огнями, глубокой ямы на дороге и других преград, которыебез выезда на полосу встречного движения, физически не получается объехать.
Можно ли выезжать пересекать прерывистую для объезда?
«Прерывистая линия» разметки 1. 5 – это наиболее любимая водителями часть дороги. Одинарной пунктирной линией разделяются участки движения на многополосных дорогах. Эту разметку можно пересекать с разных сторон, но только если такие маневры не противоречат действующим правилам дорожного движения. Например, нельзя объезжать выбоины, выезжая на другую полосу с активным движением. Можно снизить скорость и постараться аккуратно их проехать.
5 – это наиболее любимая водителями часть дороги. Одинарной пунктирной линией разделяются участки движения на многополосных дорогах. Эту разметку можно пересекать с разных сторон, но только если такие маневры не противоречат действующим правилам дорожного движения. Например, нельзя объезжать выбоины, выезжая на другую полосу с активным движением. Можно снизить скорость и постараться аккуратно их проехать.
Разрешено ли пересекать сплошную?
Без обоснованных причин, «сплошную» линию 1.1 пересекать запрещено. Исключение составляют места стоянки, парковочные площадки и край проезжей части, граничащий с обочиной. В таких случаях её можно пересекать.
Также, исключением являются неподвижные препятствия, которые своими габаритами вынуждают водителей пересекать «сплошную», объезжая их. Кроме того, разрешается совершать обгон одиночного транспортного средства с выездом на встречную полосу, если оно движется со скоростью меньшей 30 км/ч.
Спорной ситуацией является объезд автобуса по встречной полосе. По определению он не является препятствием, так что пересечение «сплошной» для его объезда на остановке, грозит штрафными санкциями. Хотя есть, конечно, один момент, когда вы можете смело оспорить свой штраф. Если между остановившимся автобусом и линией разметки 1.1 недостаточно места для проезда автомобиля, тогда его можно расценивать, как препятствие и выезжать на полосу встречного движения для объезда.
По определению он не является препятствием, так что пересечение «сплошной» для его объезда на остановке, грозит штрафными санкциями. Хотя есть, конечно, один момент, когда вы можете смело оспорить свой штраф. Если между остановившимся автобусом и линией разметки 1.1 недостаточно места для проезда автомобиля, тогда его можно расценивать, как препятствие и выезжать на полосу встречного движения для объезда.
Пересечение двойной сплошной
Излюбленное правонарушение работников дорожной полиции – пересечение «двойной сплошной». Если водитель не осведомлён в юридическом плане, тогда его легко могут лишить прав, составив соответствующий протокол. Ни для кого не секрет, что это делается только ради собственной выгоды. Но здесь можно обойтись и штрафом, а порой и вообще ничего не нарушить.
Например, на полосе вашего движения произошло ДТП. Можно ли совершить объезд аварии через двойную сплошную? Если нет физической возможности объехать препятствие справа (а автомобиль, попавший в ДТП, является препятствием), тогда при пересечении двойной сплошной, вас не имеют права привлекать к ответственности, особенно, если на месте аварии выставлен временный дорожный знак «Предварительный указатель перестроения на другую проезжую часть».
Интересный факт! Долговечность дорожной разметки проверяется количеством наездов шин, которое она выдерживает до полного истирания. Наиболее долговечная разметка наносится специальными полиуретановыми лентами. Она может выдержать до восьми миллионов наездов, в то время как обычная краска, только пятьсот тысяч.
ТЕХНИКА ВЫПОЛНЕНИЯ ОБЪЕЗДА | ОТДЕЛ ГИБДД УМВД РОССИИ ПО ГОРОДУ БРЯНСКУ
При движении на своем пути водители объезжают на дорогах автомобили и предметы, стоящие у тротуара. Приходится объезжать пешеходов и другие движущиеся объекты, а также выбоины, рытвины, кирпичи, ящики, камни и т. д. Неожиданные помехи, возникающие при объезде, требуют от водителя точности оценки обстановки, умения правильно прогнозировать развитие ситуации.
Объезд отличается от обгона тем, что объезжаемые объекты либо не двигаются, либо имеют очень небольшую скорость движения. Этот факт приводит к специфическому развитию ситуации, которая иногда бывает значительно сложнее, чем при движении на высоких скоростях. Малая скорость часто обманывает водителя.
Малая скорость часто обманывает водителя.
Одной из главных причин совершения ДТП при объезде является ошибка в оценке расстояния до автомобилей и скорости их движения, которая приводит к тому, что водитель совершает объезд, не успевает своевременно освободить полосу встречного движения,
Широко распространенной причиной происшествия при объезде является неправильный выбор траектории объезда движущегося объекта (направления объезда, интервала, дистанции до объекта). Наиболее типичной ошибкой является объезд пешехода спереди, с высокой скоростью и движением с малым интервалом.

Рекомендации. Объезжать даже частично стоящие на проезжей части автомобили и громоздкие (объемные) предметы следует с большой осторожностью и вниманием. Только убедившись в полной безопасности (даже для движения со скоростью 1—2 км/ч), можно совершать маневры объезда.
При объезде автомобилей и других объектов в местах, где вероятно появление пешеходов (магазины, кинотеатры, учреждения и т. д.), следует внимательно оценивать обстановку справа и слева, максимально увеличивать интервал и снижать скорость до безопасной. Следует проявлять повышенную осторожность при объезде в районе произвольных пешеходных переходов.
Объезжать стоящий автомобиль с выездом на полосу встречного движения можно, если расстояние до встречного автомобиля, двигающегося примерно с равной или меньшей скоростью, в 2,5-3 раза больше скорости движения автомобиля.
При объезде помех автомобилю — объектов, находящихся на проезжей части, с выездом на полосу встречного движения, оставляйте запас расстояния, чтобы завершить маневр до приближающегося транспортного средства не менее чем за 50—30 м при движении в населенном пункте.

При объезде стоящего автомобиля водителю следует включить указатель левого поворота заблаговременно до начала маневра и обязательно убедиться, что за это время не возникало помех движению, для чего необходимо оценить обстановку сзади автомобиля и перед выполнением маневра продублировать наблюдение.
Объезд транспортного средства, водитель которого подал сигнал поворота налево и приступил к выполнению маневра, производится с правой стороны.
При объезде стоящего автомобиля в первую очередь вы должны убедиться, будет ли он стоять или может начать движение и приблизиться к вам. Далее вы должны определить, не скрывается ли за ним другой участник движения: пешеход, велосипедист и т. д. — тот, кто может неожиданно появиться перед вами из-за стоящего автомобиля. В зависимости от этих двух обстоятельств вы должны сохранять меньший, или больший интервал — расстояние до стоящего автомобиля. Расстояние должно обеспечивать безопасность и быть таким, чтобы не произошло столкновение при неожиданном для вас открывании дверей этого автомобиля.
 Неприятность не угрожает вам, если в кабине нет людей. Если перед вами остановился автомобиль, вы можете с полной уверенностью предположить, что водитель откроет дверь. Он забыл или не знает, что, прежде чем открыть дверь, необходимо убедиться, что это не опасно и не создает помех для других участников’ движения.
Неприятность не угрожает вам, если в кабине нет людей. Если перед вами остановился автомобиль, вы можете с полной уверенностью предположить, что водитель откроет дверь. Он забыл или не знает, что, прежде чем открыть дверь, необходимо убедиться, что это не опасно и не создает помех для других участников’ движения.Следует также учитывать появление из-за стоящего автомобиля пешехода или, еще хуже для вас, он появится из-за промежутка между двумя стоящими автомобилями, которые вы должны объехать. Пешеходы не знают, что ПДД запрещают им это делать, поэтому вы всегда должны быть готовы подать предупредительный сигнал миганием света, чтобы на вас обратили внимание, а если ситуация будет усугубляться, то быть готовым подать звуковой сигнал и даже остановиться.
Это обусловлено тем, что при объезде пешехода сзади он будет отдаляться от траектории движения вашего автомобиля.
 При объезде же его спереди он приближается к вашей траектории и может возникнуть опасность, что ему захочется ускорить шаг или даже перебежать дорогу перед вами, что может привести к наезду на него
При объезде же его спереди он приближается к вашей траектории и может возникнуть опасность, что ему захочется ускорить шаг или даже перебежать дорогу перед вами, что может привести к наезду на негоНе пугайте пешеходов звуковым сигналом — это может усугубить обстановку на дороге. Постарайтесь войти с ним в зрительный контакт. Поэтому снижайте скорость и как можно дальше от него постарайтесь совершить этот маневр. Особенно трудно предсказуемо поведение пожилых пешеходов, пьяных и детей. По отношению к ним проявляйте особую осторожность. Если на проезжую часть выкатился мяч, ждите появления ребенка на проезжей части. Если ребенок стоит на обочине или тротуаре, он может в любой момент начать перебегать дорогу, не обращая внимания на ваш автомобиль. Пожилой человек уже забыл обязанности пешеходов, чувство бдительности у него притупилось.
Чем больше признаков, характеризующих объект объезда, вы сможете обнаружить и проанализировать, тем безопаснее будет ваш маневр.
Постоянно с помощью несложных упражнений прямо в пути вырабатывайте в себе навыки, которые могут вам пригодиться при безопасном объезде.
 упражнения для безопасного объезда:
упражнения для безопасного объезда:• двигаясь по дороге, вы увидели впереди стоящий автомобиль. Определите на глаз, сколько до него метров, затем проверьте свою оценку по счетчику;
• приближаясь к стоящему транспортному средству, особенно крупногабаритному, учитесь держать под контролем передний свес транспортного средства. Если под ним показались ноги, то приготовьтесь дать звуковой сигнал, применить экстренное торможение или совершить объезд. Если ног не видно, можно смелее объезжать стоящее транспортное средство.
Если перед вашим автомобилем неожиданно посередине проезжей части остановилось другое транспортное средство, вы, не задумываясь, должны остановить свой автомобиль. Для этого вы должны тренироваться в определении на транспортном средстве стоп-сигналов. К сожалению, они размещаются на всех транспортных средствах в разных местах, не дублируются, имеют малые размеры, загрязнены, некоторые водители их затемняют, что снижает безопасность на дорогах.
 При загорании «стопов» на впереди идущем транспортном средстве — сигнал вам: надо тормозить. Объезжать остановившееся транспортное средство с ходу ни в коем случае нельзя, перед ним могут быть пешеходы, животные, выпавший груз из других транспортных средств, иное препятствие. Объезжать это транспортное средство можно только после того, как вы убедитесь в безопасной обстановке перед ним.
При загорании «стопов» на впереди идущем транспортном средстве — сигнал вам: надо тормозить. Объезжать остановившееся транспортное средство с ходу ни в коем случае нельзя, перед ним могут быть пешеходы, животные, выпавший груз из других транспортных средств, иное препятствие. Объезжать это транспортное средство можно только после того, как вы убедитесь в безопасной обстановке перед ним.При появлении на вашем пути препятствия на узкой двухполосной дороге, прежде чем совершать объезд, вы должны подать предупредительный сигнал указателем поворота и уступить дорогу встречным транспортным средствам.
Для тренировки глазомера и возможности объезда на пути препятствия, до подъезда к этому препятствию встречного транспортного средства, поможет следующее упражнение: если вам навстречу движется транспортное средство, определите заранее, в какой точке дороги произойдет ваша встреча, а затем оцените, успели ли вы объехать стоящее до этой точки транспортное средство или нет.

Правила дорожного движения определяют: когда на пути вашего автомобиля препятствие, то вы пользуетесь преимуществом в движении, и встречные транспортные средства обязаны вам уступить дорогу в двух случаях:
• при движении на подъем при наличии знака 1.14. «Крутой подъем» вы пользуетесь преимуществом при объезде препятствия на подъеме;
• если перед препятствием есть знак 2.7. «преимущество перед встречным движением», вы также объезжаете это препятствие; пользуясь своим преимуществом.
Но в этих ситуациях, прежде чем начать маневр, убедитесь, что вам уступают дорогу. Потом труднее будет вам разбираться, кто имел преимущество.
Если вы двигаетесь по многополосной дороге в одном направлении и на вашем пути препятствие, вы обязаны уступить дорогу попутным транспортным средствам, на пути которых нет препятствия, как при объезде препятствия слева, так и при объезде препятствия справа.
Дорожный знак 4.2.2 «Объезд препятствия слева»
Думается, никто из водителей не станет спорить с тем, что объезжать возникшую на проезжей части помеху (препятствие, начало разделительной полосы, островок безопасности, направляющие островки, тумбы и прочие объекты) целесообразно именно с правой стороны, то есть по «своим» полосам.
Однако бывают случаи, когда сделать это не представляется возможным, и объезд слева является единственно приемлемым вариантом.
В подобных обстоятельствах должен выставляться дорожный знак 4.2.2 «Объезд препятствия слева».
Требования знака элементарны: водителю предписывается объезжать препятствие исключительно с левой стороны. И даже, несмотря на то, что осуществить объезд справа тоже физически возможно, ПДД четко прописывают действия водителя — только слева.
Достаточно часто знак «Объезд препятствия слева» можно встретить на автомобилях, принадлежащих коммунальным службам, предприятиям благоустройства, дорожно-ремонтным службам, которые выполняют сезонные работы по уборке дорожной территории, проводят мероприятия по ремонту дорожного полотна и пр.
Нередки случаи, когда требование знака «Объезд препятствия слева» вступает в противоречие с требованиями сплошной линии горизонтальной разметки.
В данной ситуации водитель должен помнить, что в своих действиях он должен ориентироваться на указания знака. Следовательно, ему разрешается пересечь разметку, но исключительно в целях объезда препятствия и с последующим немедленным возвращениям на ранее занимаемую полосу.
Следовательно, ему разрешается пересечь разметку, но исключительно в целях объезда препятствия и с последующим немедленным возвращениям на ранее занимаемую полосу.
И последнее. Водителю важно помнить, что в «чистом виде» знак «Объезд препятствия слева» не предоставляет приоритета транспортному средству, выполняющему объезд. Преимущество имеют транспортные средства, движущиеся во встречном направлении.
Если данная информация была для вас полезна, напишите, пожалуйста, об этом в комментариях. Если возникнут вопросы, пишите, обязательно постараемся вам помочь.
Пдд онлайн от команды autoass!
Содержание статьи:
- знак объезд препятствия слева
- дорожный знак объезд препятствия
- Знак 4 2 2
- 4 2 2 дорожный знак
Знак 4.2.1 Объезд препятствия справа
Знак 4.2.1 помогает водителям, когда на дорожном участке возникают различные препятствия. Предписывающий знак разрешает водителю ТС объезд справа.
Предписывающий знак разрешает водителю ТС объезд справа.
Представленный знак устанавливается, если на участке идут ремонтные работы. Он также говорит о начале разделительной полосы и обозначает островок безопасности. Предписывающий знак указывает четкую траекторию для объезда, за счет чего водителю проще объехать объект, мешающий привычному движению.
Зона действия предписывающего знака – месторасположение объекта, который затрудняет движение. Действие дорожного знака заканчивается после объезда препятствия. Знак 4.2.1 представляет собой синий круглый щит с белой окантовкой, на котором схематично изображена белая стрела.
Типоразмеры дорожных знаков
Типоразмер – это набор геометрических параметров дорожных знаков в зависимости от области их применения. Типоразмеры изображений знаков стандартной формы в зависимости от условий применения должны выбираться в соответствии с таблицей:
ГОСТ 32945-2014
| Типоразмер знака | Условия применения знаков |
| 1 | Автомобильные дороги с расчетной скоростью движения до 60 км/ч включительно (без усовершенствованного покрытия) |
| 2 | Автомобильные дороги с расчетной скоростью движения более 60 км/ч до 100 км/ч включительно (с усовершенствованного покрытия) |
| 3 | Автомобильные дороги с расчетной скоростью движения 120 км/ч и двумя полосами движения |
| 4 | Автомобильные дороги с расчетной скоростью движения 120 км/ч и более и четырьмя и более полосами движения |
| 5 | Места производства работ на автомобильных дорогах с расчетной скоростью движения 140 км/ч и более |
ГОСТ Р 52290-2004
| Типоразмер знака | Вне населенных пунктов | В населенных пунктах |
| I | Дороги с одной полосой | Дороги местного значения |
| II | Дороги с двумя и тремя полосами | Магистральные дороги |
| III | Дороги с четырьмя и более полосами и автомагистрали | Скоростные дороги |
| IV |
Ремонтные работы на автомагистралях, опасные участки на других дорогах при обосновании целесообразности применения.
|
|
Дорожный знак Объезд препятствия слева 4.2.2 в Ростове-на-Дону
Компания «Промышленная точка» реализует дорожные знаки для автомобильных дорог. Наша продукция предназначена для организации потоков движения и обеспечения безопасности на автомобильных дорогах и прилегающих к ним территориях. Мы реализуем знаки изготовленные по Государственному стандарту России 52290-2004. Также при необходимости можем изготовить любой знак по Вашему чертежу.
Характеристики знаков.
При производстве знаков используется оцинкованная основа, выполненная с двойной отбортовкой по краям. Используется высоко устойчивая к выгоранию пленку, что обеспечивает срок службы знак более 5 лет. При необходимости вы можете приобрести все необходимы крепления («скоба» и «коромысло») а так же столбы на которые крепятся основания знаков.
Вы можете приобрести следующие группы дорожных знаков:
Для покупки товара в нашем интернет-магазине выберите понравившийся товар и добавьте его в корзину. Далее перейдите в Корзину и нажмите на «Оформить заказ» или «Быстрый заказ».
Далее перейдите в Корзину и нажмите на «Оформить заказ» или «Быстрый заказ».
Когда оформляете быстрый заказ, напишите ФИО, телефон и e-mail. Вам перезвонит менеджер и уточнит условия заказа. По результатам разговора вам придет подтверждение оформления товара на почту или через СМС. Теперь останется только ждать доставки и радоваться новой покупке.
Оформление заказа в стандартном режиме выглядит следующим образом. Заполняете полностью форму по последовательным этапам: адрес, способ доставки, оплаты, данные о себе. Советуем в комментарии к заказу написать информацию, которая поможет курьеру вас найти. Нажмите кнопку «Оформить заказ».
Оплачивайте покупки удобным способом. В интернет-магазине доступно 3 варианта оплаты:
- Наличные при самовывозе или доставке курьером.
 Специалист свяжется с вами в день доставки, чтобы уточнить время и заранее подготовить сдачу с любой купюры. Вы подписываете товаросопроводительные документы, вносите денежные средства, получаете товар и чек.
Специалист свяжется с вами в день доставки, чтобы уточнить время и заранее подготовить сдачу с любой купюры. Вы подписываете товаросопроводительные документы, вносите денежные средства, получаете товар и чек. - Безналичный расчет при самовывозе или оформлении в интернет-магазине: карты Visa и MasterCard. Чтобы оплатить покупку, система перенаправит вас на сервер системы ASSIST. Здесь нужно ввести номер карты, срок действия и имя держателя.
- Электронные системы при онлайн-заказе: PayPal, WebMoney и Яндекс.Деньги. Для совершения покупки система перенаправит вас на страницу платежного сервиса. Здесь необходимо заполнить форму по инструкции.
Экономьте время на получении заказа. В интернет-магазине доступно 4 варианта доставки:
- Курьерская доставка в Ростове-на-Дону работает с 9.
 00 до 19.00. Когда товар поступит на склад в Ростове-на-Дону, курьерская служба свяжется для уточнения деталей. Специалист предложит выбрать удобное время доставки и уточнит адрес. Осмотрите упаковку на целостность и соответствие указанной комплектации.
00 до 19.00. Когда товар поступит на склад в Ростове-на-Дону, курьерская служба свяжется для уточнения деталей. Специалист предложит выбрать удобное время доставки и уточнит адрес. Осмотрите упаковку на целостность и соответствие указанной комплектации. - Самовывоз из магазина в Ростове-на-Дону. Список торговых точек для выбора появится в корзине. Когда заказ поступит на склад, вам придет уведомление. Для получения заказа обратитесь к сотруднику в кассовой зоне и назовите номер.
- Постамат. Когда заказ поступит на точку в Ростове-на-Дону, на ваш телефон или e-mail придет уникальный код. Заказ нужно оплатить в терминале постамата. Срок хранения — 3 дня.
- Почтовая доставка через почту России. Когда заказ придет в отделение в Ростове-на-Дону, на ваш адрес придет извещение о посылке. Перед оплатой вы можете оценить состояние коробки: вес, целостность. Вскрывать коробку самостоятельно вы можете только после оплаты заказа. Один заказ может содержать не больше 10 позиций и его стоимость не должна превышать 100 000 р.

обл Ростовская, г Ростов-на-Дону, ул Шаумяна, дом 47, корп. В
Пн-Пт 10.00-19.00 Сб 10.00-15.00 Вс выходной
обл Ростовская, г Ростов-на-Дону, ул Мильчакова, дом 45
ежедневно 10.00-21.00
обл Ростовская, г Ростов-на-Дону, ул Зорге, дом 39
Пн-Пт 10.00-20.00 Сб,Вс 10.00-18.00
обл Ростовская, г Ростов-на-Дону, ул Таганрогская, дом 132/3
ежедневно 10. 00-20.00
00-20.00
обл Ростовская, г Ростов-на-Дону, пр-кт 40-летия Победы, дом 332Б
Пн-Пт 09.00-18.00 Сб 13.00-19.00 Вс выходной
обл Ростовская, г Ростов-на-Дону, ул Мечникова, дом 31
ежедневно 09.00-20.00
обл Ростовская, г Ростов-на-Дону, ул 35-я Линия, дом 83/75
ежедневно 10.00-21.00
обл Ростовская, г Ростов-на-Дону, ул Казахская, дом 121
Пн-Пт 10.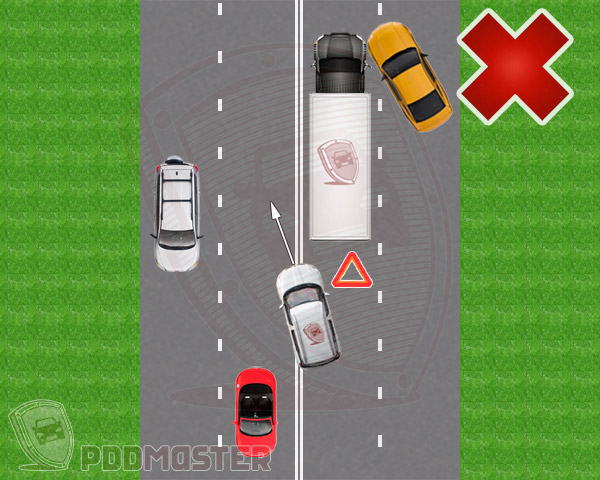 00-21.00 Сб,Вс 10.00-18.00
00-21.00 Сб,Вс 10.00-18.00
обл Ростовская, г Ростов-на-Дону, пр-кт Буденновский, влад. 93А/220
ежедневно 09.00-21.00
обл Ростовская, г Ростов-на-Дону, ул Ткачева, дом 22
ежедневно 09.00-21.00
Подробнее о вариантах доставкиДорожный знак 4.
 2.2 «Объезд препятствия слева»
2.2 «Объезд препятствия слева»Любое препятствие, будь то островок безопасности, начало разделительной полосы, дорожная тумба или какой-либо другой объект, водители обычно стараются объехать справа, то есть, по своей полосе движения. Однако бывают обстоятельства, когда объезд справа является невозможным, и тогда единственным способом преодоления препятствия является его объезд с левой стороны.
В подобных ситуациях на дороге устанавливается предписывающий дорожный знак 4.2.2 «Объезд препятствия слева».
Как и другие знаки данной категории, знак 4.2.2 имеет круглую форму и синий цвет с белой окантовкой. На знаке изображена белая стрелка, указывающая сверху вниз, справа налево.
Предписание данного знака совершенно понятно: препятствие разрешается объезжать только слева. И даже если имеется возможность объехать его справа, делать этого не следует.
Нередко знаком «Объезд слева» оборудуются машины, которые принадлежат коммунальным предприятиям и другим службам, обеспечивающим благоустройство улиц, проводящим уборочные или ремонтные работы или осуществляющим полив зелёных насаждений. В данном случае требование знака может ступать в противоречие с дорожной разметкой: сплошной одинарной или двойной горизонтальной полосой. В подобных ситуациях водители обязаны руководствоваться именно указаниями знака, а не разметки. То есть, они в целях объезда имеют право пересечь сплошную полосу, однако сразу же по завершению манёвра вернуться на полосу, занимаемую ранее.
В данном случае требование знака может ступать в противоречие с дорожной разметкой: сплошной одинарной или двойной горизонтальной полосой. В подобных ситуациях водители обязаны руководствоваться именно указаниями знака, а не разметки. То есть, они в целях объезда имеют право пересечь сплошную полосу, однако сразу же по завершению манёвра вернуться на полосу, занимаемую ранее.
Водители должны понимать и то, что знак 4.2.2 «Объезд препятствия слева» не предоставляет им преимущества, которое в данном случае находится на стороне транспортных средств, движущихся во встречном направлении.
Читайте также:
– Дорожный знак 4.2.3 «Объезд препятствия справа или слева»
– Дорожный знак 4.3 «Круговое движение»
– Дорожный знак 4.4.1 «Велосипедная дорожка или полоса для велосипедистов»
границ | Следование по пути, обнаружение препятствий и уклонение от препятствий для подводных роботов-змей
1. Введение
За миллионы лет эволюции морские змеи, угри и рыбы развили высокоэффективное движение для движения и передвижения. Эти существа способны быстро менять направление и очень эффективно (Lighthill, 1970, 1975). Многие из них обладают превосходными способностями к ускорению, одновременно имея возможность выходить в замкнутые пространства, используя свои гибкие тела.За последние десятилетия дистанционно управляемые транспортные средства (ROV) широко использовались для подводных инспекций, технического обслуживания и ремонта в нефтегазовой отрасли (Christ and Wernli, 2013). Эти транспортные средства полагаются на то, что ими управляет высококвалифицированный человек. Чтобы сделать такие операции более безопасными и более рентабельными, растет интерес к разработке интервенционных АНПА (I-AUV) (Ridao et al., 2014), подводных роботов-змей (USR) (Mclsaac and Ostrowski, 1999; McIsaac, Ostrowski, 2002; Такаяма, Хиросе, 2002; Wilbur et al., 2002; Креспи и др., 2005; Ямада и др., 2005; Креспи и Эйспеерт, 2006; Ли и др., 2011; Стефанини и др., 2012; Liljebäck et al., 2014; Kelasidi et al., 2016a, b) и подводных роботов-змей с подруливающими устройствами (Sverdrup-Thygeson et al.
Эти существа способны быстро менять направление и очень эффективно (Lighthill, 1970, 1975). Многие из них обладают превосходными способностями к ускорению, одновременно имея возможность выходить в замкнутые пространства, используя свои гибкие тела.За последние десятилетия дистанционно управляемые транспортные средства (ROV) широко использовались для подводных инспекций, технического обслуживания и ремонта в нефтегазовой отрасли (Christ and Wernli, 2013). Эти транспортные средства полагаются на то, что ими управляет высококвалифицированный человек. Чтобы сделать такие операции более безопасными и более рентабельными, растет интерес к разработке интервенционных АНПА (I-AUV) (Ridao et al., 2014), подводных роботов-змей (USR) (Mclsaac and Ostrowski, 1999; McIsaac, Ostrowski, 2002; Такаяма, Хиросе, 2002; Wilbur et al., 2002; Креспи и др., 2005; Ямада и др., 2005; Креспи и Эйспеерт, 2006; Ли и др., 2011; Стефанини и др., 2012; Liljebäck et al., 2014; Kelasidi et al., 2016a, b) и подводных роботов-змей с подруливающими устройствами (Sverdrup-Thygeson et al. , 2016a, b) как шаг к повышению автономности, ловкости и точности для задач подводных манипуляций. Подробные обсуждения различных подводных робототехнических систем, таких как ROV, AUV и биоиндуцированные роботизированные системы, можно найти в Kelasidi et al. (2016a) и Kelasidi et al.(2017b).
, 2016a, b) как шаг к повышению автономности, ловкости и точности для задач подводных манипуляций. Подробные обсуждения различных подводных робототехнических систем, таких как ROV, AUV и биоиндуцированные роботизированные системы, можно найти в Kelasidi et al. (2016a) и Kelasidi et al.(2017b).
Вдохновленный биологическими плавающими существами, новая концепция био-вдохновленных мультисочлененных роботизированных систем была проиллюстрирована на Рисунке 1, который сочетает в себе свойства водных животных с современными решениями морских технологий. В отличие от обычных подводных роботов, USR — это тонкий робот с высокой степенью избыточности, который может продвигаться вперед, используя волнообразные движения тела в сочетании с хвостовым, спинным и грудным плавниками и / или с кормовыми гребными винтами и туннельными подруливающими устройствами вдоль тела.Это обеспечивает значительную гибкость и увеличивает маневренность робота для подводных применений, как показано на рисунке 1 (Kelasidi et al. , 2015; Sverdrup-Thygeson et al., 2016b). Модульная конструкция робота делает его пригодным для различных применений, просто соединяя различные модули в различных комбинациях для создания различных типов транспортных средств. Как показано на Рисунке 1, роботизированная система представляет собой маневренную роботизированную руку, которая может управлять инструментами и выполнять легкие задачи вмешательства.Кроме того, с помощью крыльев или двигателей он может перемещаться на большие расстояния аналогично исследовательскому АПА, а его гибкий и тонкий корпус обеспечивает возможность доступа и работы в ограниченных областях подводных сооружений. Модульная конструкция робота делает его применимым для различных приложений в зависимости от требований задачи. Например, чисто биологическое решение без использования пропеллеров может быть рассмотрено для приложений, где требуется ограниченный акустический шум, тогда как оснащение робота подруливающими устройствами может обеспечить улучшенную маневренность для задач проверки и вмешательства.
, 2015; Sverdrup-Thygeson et al., 2016b). Модульная конструкция робота делает его пригодным для различных применений, просто соединяя различные модули в различных комбинациях для создания различных типов транспортных средств. Как показано на Рисунке 1, роботизированная система представляет собой маневренную роботизированную руку, которая может управлять инструментами и выполнять легкие задачи вмешательства.Кроме того, с помощью крыльев или двигателей он может перемещаться на большие расстояния аналогично исследовательскому АПА, а его гибкий и тонкий корпус обеспечивает возможность доступа и работы в ограниченных областях подводных сооружений. Модульная конструкция робота делает его применимым для различных приложений в зависимости от требований задачи. Например, чисто биологическое решение без использования пропеллеров может быть рассмотрено для приложений, где требуется ограниченный акустический шум, тогда как оснащение робота подруливающими устройствами может обеспечить улучшенную маневренность для задач проверки и вмешательства. Использование USR для таких подводных операций ставит несколько интересных исследовательских задач. На рисунке 2 показан первый USR, оснащенный двигателями в хвостовом модуле, разработанный в Норвежском университете науки и технологий (NTNU) (Liljebäck et al., 2014; Kelasidi et al., 2016b). Эта роботизированная платформа, использующая подруливающие устройства только в хвостовом модуле, может считаться частным случаем общей концепции, показанной на рисунке 1, и является шагом к разработке следующего поколения USR с дополнительными эффекторами.Модульный робот-змея Мамба (Liljebäck et al., 2014) может быть оснащен подруливающими устройствами при работе под водой (Kelasidi et al., 2016b). Мамба с двигателями — это новый тип змееподобного робота, который сочетает в себе волнообразное движение, вызванное биологическими методами, с использованием двигателей, и является испытательной платформой, рассматриваемой для всех экспериментальных результатов, представленных в этой статье.
Использование USR для таких подводных операций ставит несколько интересных исследовательских задач. На рисунке 2 показан первый USR, оснащенный двигателями в хвостовом модуле, разработанный в Норвежском университете науки и технологий (NTNU) (Liljebäck et al., 2014; Kelasidi et al., 2016b). Эта роботизированная платформа, использующая подруливающие устройства только в хвостовом модуле, может считаться частным случаем общей концепции, показанной на рисунке 1, и является шагом к разработке следующего поколения USR с дополнительными эффекторами.Модульный робот-змея Мамба (Liljebäck et al., 2014) может быть оснащен подруливающими устройствами при работе под водой (Kelasidi et al., 2016b). Мамба с двигателями — это новый тип змееподобного робота, который сочетает в себе волнообразное движение, вызванное биологическими методами, с использованием двигателей, и является испытательной платформой, рассматриваемой для всех экспериментальных результатов, представленных в этой статье.
Рисунок 1 . Подводные роботы-змеи очень гибкие, способны быстро менять направление и могут получать доступ к небольшим и замкнутым пространствам.Они могут выполнять задачи вмешательства и эффективную транспортировку для миссий на большие расстояния. В сочетании с дополнительными исполнительными механизмами, такими как подруливающие устройства или хвостовые стабилизаторы, эти роботы очень универсальны и могут применяться для множества подводных операций. (A) Концепт представляет собой био-вдохновленные подводные роботы-змеи с дополнительными эффекторами. (B) Новое поколение диагностических и ремонтных машин для подводного применения.
Подводные роботы-змеи очень гибкие, способны быстро менять направление и могут получать доступ к небольшим и замкнутым пространствам.Они могут выполнять задачи вмешательства и эффективную транспортировку для миссий на большие расстояния. В сочетании с дополнительными исполнительными механизмами, такими как подруливающие устройства или хвостовые стабилизаторы, эти роботы очень универсальны и могут применяться для множества подводных операций. (A) Концепт представляет собой био-вдохновленные подводные роботы-змеи с дополнительными эффекторами. (B) Новое поколение диагностических и ремонтных машин для подводного применения.
Рисунок 2 .Различные конфигурации подводного робота-змеи Мамба.
Обход препятствий — важная задача для многих робототехнических систем. Для систем с фиксированным основанием робот должен избегать самоуничтожения, а также любых объектов, которые могут находиться в его рабочем пространстве. Для роботов с плавающей базой, таких как USR или надводный корабль, основная задача — избегать стационарных и динамических препятствий, таких как острова / трубопроводы / другие конструкции и другие корабли или системы плавучих баз. Существует несколько алгоритмов планирования пути для расчета безопасного пути для избежания препятствий, таких как A ⋆ , RRT и HBug (Hernandez et al., 2015). Однако эти методы глобального планирования пути не подходят для неизвестных и динамичных сред и должны быть дополнены локальной системой наведения, которая позволяет мобильной роботизированной системе избегать небольших, непредвиденных и динамических препятствий при следовании по глобальному пути. Было предложено множество таких локальных подходов как для общего, так и для морского случая, таких как потенциальные поля (Khatib, 1985), динамическое окно (Fox et al., 1997; Loe, 2008), скоростные препятствия van den Berg et al. .(2011); Kuwata et al. (2014) и Tangent / WedgeBug Laubach and Burdick (1999).
Для роботов с плавающей базой, таких как USR или надводный корабль, основная задача — избегать стационарных и динамических препятствий, таких как острова / трубопроводы / другие конструкции и другие корабли или системы плавучих баз. Существует несколько алгоритмов планирования пути для расчета безопасного пути для избежания препятствий, таких как A ⋆ , RRT и HBug (Hernandez et al., 2015). Однако эти методы глобального планирования пути не подходят для неизвестных и динамичных сред и должны быть дополнены локальной системой наведения, которая позволяет мобильной роботизированной системе избегать небольших, непредвиденных и динамических препятствий при следовании по глобальному пути. Было предложено множество таких локальных подходов как для общего, так и для морского случая, таких как потенциальные поля (Khatib, 1985), динамическое окно (Fox et al., 1997; Loe, 2008), скоростные препятствия van den Berg et al. .(2011); Kuwata et al. (2014) и Tangent / WedgeBug Laubach and Burdick (1999). Однако у этих подходов есть несколько недостатков. Потенциальные поля могут страдать от колебательного поведения и сходимости к локальным минимумам (Корен и Боренштейн, 1991), а метод динамического окна может быть трудоемким в вычислительном отношении. Подход с использованием скоростных препятствий (VO) обладает хорошими математическими качествами и прост в вычислительном отношении, но его нелегко реализовать. Однако основным недостатком этих методов является тот факт, что неочевидно, как сочетать эти методы предотвращения столкновений с существующими, обычно используемыми методами наведения для следования по пути, такими как прямая видимость (LOS) (Fossen, 2011).Алгоритм Wedgebug применяется к марсоходам и предполагает, что марсоход моделируется как точечный робот в двухмерной двоичной среде (т. Е. Каждая точка в окружающей среде либо содержится в непроходимом препятствии, либо находится в свободном пространстве) и что границы препятствия блокируются. ощущение, а также движение. В подходе, предложенном в этой статье, границы препятствий могут быть виртуальными, что предотвращает переход в идентифицированные небезопасные зоны без физических препятствий на пути.
Однако у этих подходов есть несколько недостатков. Потенциальные поля могут страдать от колебательного поведения и сходимости к локальным минимумам (Корен и Боренштейн, 1991), а метод динамического окна может быть трудоемким в вычислительном отношении. Подход с использованием скоростных препятствий (VO) обладает хорошими математическими качествами и прост в вычислительном отношении, но его нелегко реализовать. Однако основным недостатком этих методов является тот факт, что неочевидно, как сочетать эти методы предотвращения столкновений с существующими, обычно используемыми методами наведения для следования по пути, такими как прямая видимость (LOS) (Fossen, 2011).Алгоритм Wedgebug применяется к марсоходам и предполагает, что марсоход моделируется как точечный робот в двухмерной двоичной среде (т. Е. Каждая точка в окружающей среде либо содержится в непроходимом препятствии, либо находится в свободном пространстве) и что границы препятствия блокируются. ощущение, а также движение. В подходе, предложенном в этой статье, границы препятствий могут быть виртуальными, что предотвращает переход в идентифицированные небезопасные зоны без физических препятствий на пути.
В морской навигации существует несколько методов уклонения от препятствий, каждый из которых требует некоторой информации о самом препятствии, т.е.е., положение, размер и / или скорость. Для обнаружения подводных препятствий можно использовать датчики, такие как гидролокаторы и камеры (Nicholson, Healey, 2008; Ridao et al., 2014; Mallios et al., 2016). Из-за свойств распространения света под водой часто применяются методы навигации, основанные на акустике. Системы обзора уменьшают дальность, но также уменьшают пространство и стоимость, а также увеличивают разрешение (Bonin-Font et al., 2008). Часто системы технического зрения основаны на двух камерах, то есть стереозрении. С такой настройкой можно использовать сопоставление и геометрическую триангуляцию для расчета трехмерного положения обнаруженных объектов (Goldberg et al., 2002). USR Mamba оснащена одиночной камерой в головном модуле. Однако для обхода препятствий по-прежнему требуется определение глубины, то есть расстояния между датчиком обзора и препятствием. Чтобы добиться этого с помощью монокулярного зрения, нужно полагаться на предположения относительно геометрии сцены и движения транспортного средства (Bhatti, 2008; Lei et al., 2013). В этой статье мы разработали алгоритм компьютерного зрения для обнаружения потенциальных препятствий на пути USR с помощью единственной камеры, прикрепленной к головному модулю робота, и отражающих маркеров на препятствиях.Площадь маркеров известна априори и может использоваться для расчета трехмерного расстояния на основе соответствующей области на изображении, аналогично Bousaid et al. (2016). Различные геометрические формы (например, треугольник, квадрат и круг). Это можно использовать для классификации различных типов препятствий. Форма определяется путем анализа кривизны формы и подсчета количества выступов.
Чтобы добиться этого с помощью монокулярного зрения, нужно полагаться на предположения относительно геометрии сцены и движения транспортного средства (Bhatti, 2008; Lei et al., 2013). В этой статье мы разработали алгоритм компьютерного зрения для обнаружения потенциальных препятствий на пути USR с помощью единственной камеры, прикрепленной к головному модулю робота, и отражающих маркеров на препятствиях.Площадь маркеров известна априори и может использоваться для расчета трехмерного расстояния на основе соответствующей области на изображении, аналогично Bousaid et al. (2016). Различные геометрические формы (например, треугольник, квадрат и круг). Это можно использовать для классификации различных типов препятствий. Форма определяется путем анализа кривизны формы и подсчета количества выступов.
В этой статье мы проводим эксперименты, чтобы исследовать как отслеживание пути, так и проблему управления обходом препятствий с использованием USR Mamba с подруливающими устройствами (Kelasidi et al. , 2016б). Цель экспериментов — обнаружить потенциальные препятствия на пути и спроектировать движение USR, чтобы гарантировать, что робот может сходиться и следовать по заранее заданному контрольному пути, избегая обнаруженных препятствий.
, 2016б). Цель экспериментов — обнаружить потенциальные препятствия на пути и спроектировать движение USR, чтобы гарантировать, что робот может сходиться и следовать по заранее заданному контрольному пути, избегая обнаруженных препятствий.
In Kelasidi et al. (2016b), предлагается, чтобы для обеспечения эффективной транспортировки, USR с подруливающими устройствами в хвостовом модуле в основном использовал подруливающие устройства для передвижения, в то время как многосочлененный корпус должен использоваться для управления направлением. Руководствуясь этими результатами, мы предлагаем стратегию управления перемещением USR с общей целью исследования его способности следовать заданной опорной траектории.В нескольких предыдущих работах рассмотрены схемы управления перемещением USR без подруливающих устройств. Сравнение этих подходов представлено в Kelasidi et al. (2017b) и Kelasidi et al. (2016a). Кроме того, в Sans-Muntadas et al. Описан подход к стыковке для толкаемых USR с использованием углов сочленения для управления направлением робота.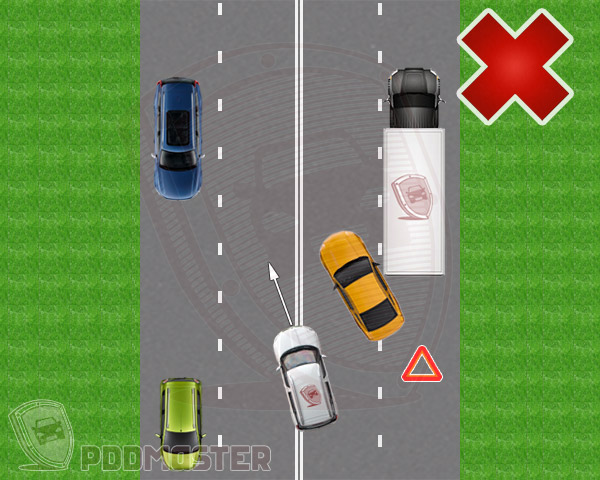 (2017).
(2017).
В этом документе представлена стратегия управления следования по траектории, позволяющая заставить USR двигаться по желаемой опорной траектории. Кроме того, разработанная схема обнаружения препятствий была успешно применена и объединена с методом предотвращения столкновений на основе набора (Moe, Pettersen, 2016; Kohl et al., 2017). Такой подход обеспечивает обход препятствий, когда это необходимо, и следование пути в противном случае.
Концепция управления траекторией и предотвращение препятствий для USR без подруливающих устройств была исследована в Kohl et al. (2017). Здесь и направление, и толчок достигаются за счет волнообразного движения суставов. В данной статье эти методы адаптированы к USR с подруливающими устройствами. Кроме того, представлена стратегия обнаружения препятствий, совмещенная с методами следования по пути и обхода препятствий.Предлагаемая стратегия наведения и управления, а также стратегия обнаружения и уклонения от препятствий проверены экспериментально для USR с подруливающими устройствами. Насколько известно авторам, экспериментальные результаты, касающиеся обнаружения и уклонения от препятствий, не были представлены в предыдущей литературе для USR с опорой.
Насколько известно авторам, экспериментальные результаты, касающиеся обнаружения и уклонения от препятствий, не были представлены в предыдущей литературе для USR с опорой.
Этот документ организован следующим образом: Раздел 2 представляет экспериментальную установку, а также методы наведения и контроля для следования по траектории и обхода препятствий, а также алгоритм обнаружения препятствий.В разделе 3 представлены и обсуждаются экспериментальные результаты. Выводы приведены в разделе 4.
2. Система настройки и управления
В этом разделе мы даем краткое описание надводного USR Mamba и экспериментальной установки. Кроме того, мы обсуждаем и представляем, как подход к наведению и управлению, предложенный ранее для USR без подруливающих устройств, адаптирован к экспериментам с управляемой Mamba. Наконец, представлены метод обнаружения препятствий, принятый в этой статье, и подход к обходу препятствий на основе набора, предложенный для толкаемых USR.
2.
 1. Экспериментальная установка
1. Экспериментальная установка Подводный робот-змея с подруливающими устройствами в хвостовом модуле по имени Мамба (рис. 2), по сути, представляет собой самоходную роботизированную руку с тонким и гибким корпусом, способную выполнять задачи проверки в ограниченном пространстве, недоступном для обычных подводных аппаратов. Мамба имеет модульную конструкцию и может работать на небольшой глубине. Для получения дополнительной информации о роботе см. Kelasidi et al. (2016а, б). Обратите внимание, что для управляемого робота важно знать амплитуду приложенных сил подруливающего устройства как функцию конкретного управляющего воздействия.Первоначальные эксперименты были выполнены для получения необходимого отображения от входов двигателя u c к усилиям двигателя F t для USR, и результаты доказывают, что зависимость является довольно линейной (Kelasidi et al. ., 2016б). Другая чисто биологическая конфигурация подводного робота-змеи Мамба с пассивным хвостовым плавником, прикрепленным к хвостовому модулю робота (рис. 2), может быть выгодна по сравнению с конфигурацией с подруливающими устройствами, поскольку она не производит значительного акустического шума.Более того, конфигурация плавников не будет беспокоить окружающую среду так сильно, как двигатели, что очень актуально для таких приложений, как археологическое исследование затонувших кораблей и неинвазивный мониторинг морской флоры и фауны. Сравнительное исследование робота с хвостовым плавником и без него было представлено в Kelasidi et al. (2017a). В частности, было показано, что прикрепив пассивный хвостовой плавник, можно вдвое увеличить скорость движения вперед. Это значительное увеличение скорости требует относительно небольшого увеличения энергопотребления и достигается при минимальном увеличении сложности механической конструкции.
2), может быть выгодна по сравнению с конфигурацией с подруливающими устройствами, поскольку она не производит значительного акустического шума.Более того, конфигурация плавников не будет беспокоить окружающую среду так сильно, как двигатели, что очень актуально для таких приложений, как археологическое исследование затонувших кораблей и неинвазивный мониторинг морской флоры и фауны. Сравнительное исследование робота с хвостовым плавником и без него было представлено в Kelasidi et al. (2017a). В частности, было показано, что прикрепив пассивный хвостовой плавник, можно вдвое увеличить скорость движения вперед. Это значительное увеличение скорости требует относительно небольшого увеличения энергопотребления и достигается при минимальном увеличении сложности механической конструкции.
Робот, рассматриваемый в данном исследовании, состоит из 18 шарниров, установленных с относительной ориентацией 90 градусов попеременно для достижения как рыскания, так и тангажа (Liljebäck et al., 2014). Во время экспериментов использовалась внешняя оболочка, чтобы создать дополнительный водный барьер, а также сделать внешнюю поверхность робота более гладкой. Схема экспериментальной установки показана на рисунке 3.
Во время экспериментов использовалась внешняя оболочка, чтобы создать дополнительный водный барьер, а также сделать внешнюю поверхность робота более гладкой. Схема экспериментальной установки показана на рисунке 3.
Рисунок 3 . Экспериментальная установка для исследования пути следования за контролем и обнаружения препятствий и уклонения от препятствий с помощью подводного робота-змеи Мамба.
Эксперименты, проведенные в бассейне Лаборатории морской кибернетики (MC-lab), Тронхейм, Норвегия (MCl, 2018). Котловина имеет глубину 1,5 м, площадь поверхности 40 м × 6,45 м. Шесть подводных камер Qualisys (QUA, 2018) использовались для отслеживания и регистрации положения и ориентации θ робота с использованием конструкции с отражающими маркерами, прикрепленными к головному или хвостовому модулю. Центр масс (CM) p x , p y затем вычисляется с использованием кинематических уравнений робота (Kelasidi et al. , 2016а). Как показано на Рисунке 3, полученные измерения были использованы для исследования различных проблем управления подводным роботом-змеей Мамба. Во время этих экспериментов углы сочленений, ответственные за вертикальное (тангажное) движение, были установлены на ноль градусов для достижения чисто горизонтального движения. Все алгоритмы были реализованы на внешнем компьютере с использованием Labview, а необходимые сигналы отправлялись / принимались на / от робота через соединение CAN-шины через трос. На рисунке 3 показаны три различных тематических исследования для USR с подруливающими устройствами: (1) Исследования эффективности передвижения Kelasidi et al.(2016b), (2) Следование по траектории USR с подруливающими устройствами и (3) Стратегия переключения между режимами следования по траектории и режимами обнаружения препятствий и избегания препятствий, разработанная и экспериментально подтвержденная в этой статье. В следующих разделах каждая часть тематических исследований, показанных на Рисунке 3, будет рассмотрена более подробно.
, 2016а). Как показано на Рисунке 3, полученные измерения были использованы для исследования различных проблем управления подводным роботом-змеей Мамба. Во время этих экспериментов углы сочленений, ответственные за вертикальное (тангажное) движение, были установлены на ноль градусов для достижения чисто горизонтального движения. Все алгоритмы были реализованы на внешнем компьютере с использованием Labview, а необходимые сигналы отправлялись / принимались на / от робота через соединение CAN-шины через трос. На рисунке 3 показаны три различных тематических исследования для USR с подруливающими устройствами: (1) Исследования эффективности передвижения Kelasidi et al.(2016b), (2) Следование по траектории USR с подруливающими устройствами и (3) Стратегия переключения между режимами следования по траектории и режимами обнаружения препятствий и избегания препятствий, разработанная и экспериментально подтвержденная в этой статье. В следующих разделах каждая часть тематических исследований, показанных на Рисунке 3, будет рассмотрена более подробно.
2.2. Управление и контроль
Система наведения и управления USR показана на рисунке 3, а определение математических символов описано в таблице 1.Система наведения предоставляет ссылку θ или для ориентации USR, которой контроллер пытается следовать, управляя соединениями USR. Подруливающие устройства управляются входом u c , и каждое соединение следует за выходом контроллера направления ϕ 0 согласно (1). Предлагаемая стратегия управления предполагает, что суставы робота используются для управления направлением, в то время как движение робота осуществляется только подруливающими устройствами.Это независимая система, в которой значения управляющего входа uc отвечают за управление поступательной скоростью робота, а контроллер направления (1) отвечает за поворот робота.
Таблица 1 . Определение математических терминов.
Уклонение от препятствий по своей природе является функцией безопасности, которую следует активировать при необходимости и иначе не влиять на поведение системы. В этом документе режимом работы по умолчанию является следование по прямой линии, хотя эта цель может быть легко заменена другим режимом работы, который будет объединен с предлагаемым методом обхода препятствий.Для получения дополнительной информации см. Раздел 2.3 и Moe and Pettersen (2016). Чтобы создать систему наведения со следованием по пути и режимом уклонения от препятствий, мы используем закон наведения от Kohl et al. (2017), который подходит как для следования по прямой, так и для круговой траектории. Последний применяется для объезда препятствий на пути.
В этом документе режимом работы по умолчанию является следование по прямой линии, хотя эта цель может быть легко заменена другим режимом работы, который будет объединен с предлагаемым методом обхода препятствий.Для получения дополнительной информации см. Раздел 2.3 и Moe and Pettersen (2016). Чтобы создать систему наведения со следованием по пути и режимом уклонения от препятствий, мы используем закон наведения от Kohl et al. (2017), который подходит как для следования по прямой, так и для круговой траектории. Последний применяется для объезда препятствий на пути.
Препятствия можно избежать за счет того, что USR всегда поддерживает определенное безопасное расстояние между собой и препятствием. Таким образом, в нашей системе наведения для уклонения от препятствий мы предлагаем окружить препятствие, центральное положение которого определяется как P o = [ P ox , P oy] T , с виртуальным окружность радиуса R s . Центр окружности закреплен в центре препятствия, а радиус выбран достаточно большим, чтобы, если USR находится снаружи или на R s , столкновения не произойдет. Следовательно, R s упоминается как безопасный радиус, и формализованная цель управления объездом препятствия состоит в том, чтобы гарантировать, что USR всегда находится снаружи или на R s .
Центр окружности закреплен в центре препятствия, а радиус выбран достаточно большим, чтобы, если USR находится снаружи или на R s , столкновения не произойдет. Следовательно, R s упоминается как безопасный радиус, и формализованная цель управления объездом препятствия состоит в том, чтобы гарантировать, что USR всегда находится снаружи или на R s .
В предыдущей литературе изучалось множество различных подходов к управлению по траектории для USR без подруливающих устройств (McIsaac and Ostrowski, 2003; Lapierre and Jouvencel, 2005; Alamir et al., 2007; Kelasidi et al., 2016a, 2017b). Вводное обсуждение, сравнивающее различные подходы к управлению, изученные для подводных плавательных роботов, можно найти в (Kelasidi et al., 2016a, 2017b). В этой статье мы представляем экспериментальные результаты для подводного робота-змеи Мамба с подруливающими устройствами в хвостовом модуле с использованием подхода управления по траектории, описанного ниже.
Подход к управлению состоит из пути следования закону наведения, отвечающего за создание эталонной ориентации θ ref, pf , контроллера курса, отвечающего за то, чтобы фактическая ориентация θ отслеживала эталонную ориентацию, и управляющего входа u c к двигателям, ответственным за продвижение робота вперед.Эталонная ориентация θ ref, pf робота рассчитывается с использованием закона наведения, представленного в (1), который для следования по прямой линии сводится к хорошо известному закону наведения LOS. Подход LOS основан на понятии, ведущем рассматриваемое транспортное средство по желаемому пути, а другое — на пути. Последнее сводится к нулю, когда транспортное средство движется по заданному пути, и обычно используется как для морских транспортных средств (Børhaug, Pettersen, 2006; Breivik and Fossen, 2008), так и для USR (Kelasidi et al., 2016а, 2017б).
В этом документе опорный путь совмещен с мировой осью x . Следовательно, положение y USR p y определяется как ошибка пересечения пути для следования по пути. Ориентация робота была измерена с помощью системы позиционирования подводной камеры, как показано на рисунке 3, путем прикрепления отражающих маркеров к хвостовому модулю робота. Контроллер направления (2) используется для создания смещения угла сочленения ϕ 0 , которое отправляется роботу через CAN.
Существует несколько возможных определений ориентации USR (Kelasidi et al., 2016a; Kohl et al., 2016). В этой статье ориентация θ робота определяется как ориентация угла головы θ: = θ N . В экспериментальной установке положение и ориентация USR измеряются с помощью системы подводного позиционирования в лаборатории (см. Рисунок 3). Эталонная ориентация определяется следующим руководящим законом (Kohl et al., 2017):
θref = arctan (μyμx), μ (p) = — dhpT‖dhp‖2 (ktranh (p)) + ν [0110] dhpTkalong‖dhp‖, ν = {- 1, круг против часовой стрелки + 1, круг по часовой стрелке (1)Здесь h ( p ) — это функция стоимости, которая неявно определяет опорный путь, dhpT = ∇h (p) — вектор, нормальный для наборов уровней h , k tran — поперечное усиление, а k вдоль — продольное усиление.Этот опорный угол обозначается как θ ref, pf и используется как опорный для отслеживания пути (см. Рисунок 3).
Поскольку dhpT = ∇h (p) перпендикулярно наборам уровней h (·), закон управления (1) может быть интуитивно описан следующим образом. Эталонная скорость μ ( p ) состоит из двух компонентов: первая компонента перпендикулярна наборам уровней h (·) и уменьшает расстояние от центра масс до кривой γ = h −1 (0).Вторая составляющая касается наборов уровней h (·) и регулирует скорость центра масс на кривой γ = h −1 (0). Выбор ν позволяет нам выбрать направление, в котором робот должен двигаться вокруг препятствия.
Аналогично, угол θ ref, oa , полученный из (1) с использованием hoa (p) = (px-pox) 2+ (py-poy) 2-Rs2, используется в качестве эталона для уклонения от препятствий. В этом случае параметр ν управляет направлением движения USR и выбирается таким образом, чтобы USR обходил препятствие, отклоняясь как можно меньше от опорной прямой.Обратите внимание, что для этой схемы наведения достаточно знать положение препятствия относительно USR. Однако в этой статье мы вычислили положение препятствий в мире, потому что препятствия обнаруживаются относительно кадра камеры (прикрепленного к головному звену USR), тогда как положение USR указывается как CM.
При применении к прямой линии закон наведения (1) гарантирует, что USR сходится к опорному пути. Однако для круговой траектории закон наведения (1) гарантирует, что робот приближается к траектории и после этого остается рядом с ней с постоянным смещением за пределами радиуса R s .
Замечание 1 . Обратите внимание, что смещение можно сделать небольшим, увеличив k tran , или полностью исключить, добавив интегральное действие к закону наведения. Однако в этой статье мы намеренно выбираем довольно маленький k tran и, таким образом, всегда сохраняем USR безопасно за пределами круга, вместо того, чтобы гарантировать, что он сходится ближе к безопасному радиусу R s и, возможно, вылетает за пределы круга. .
Последней частью системы навигации является алгоритм, который определяет, является ли активным режимом следование по траектории или уклонение от препятствий.Более подробно это описано в разделе 2.3.
In Sans-Muntadas et al. (2017) предлагается установить эталон для каждого стыка как
, т.е. чтобы каждое соединение имело одинаковое значение, обеспечивая равномерную кривизну по всему роботу. Это отличается от Kohl et al. (2017), где для движения используются волнообразные формы, а ссылки на соединения включают дополнительный синусоидальный член со сдвигом фаз между соединениями. Вместо этого (1) гарантирует, что шарниры используются только для управления направлением, в то время как подруливающие устройства используются для продвижения робота вперед.В частности, Sans-Muntadas et al. (2017) показали, что с помощью (1) роботу удалось хорошо сходиться и двигаться по желаемому пути. Следовательно, чтобы направить толкаемый USR в исходную ориентацию, параметр ϕ 0 используется для управления направлением робота. Чтобы управлять ориентацией θ в соответствии с законом управления (1), следующий контроллер PD используется для определения смещения угла сустава (Kohl et al., 2017):
ϕ0 = kp (θref-θ) + kd (θ.ref-θ.) (3)В приведенном выше уравнении коэффициенты усиления управления k p и k d являются постоянными и положительными.Кроме того, чтобы гарантировать, что угол стыка ϕ i отслеживает опорный сигнал ϕi * = ϕ0, в микроконтроллеры внутри каждого модуля Mamba встроен П-контроллер низкого уровня. Точно так же, чтобы назначить скорость вращения двигателям, реализован соответствующий контроллер низкого уровня, чтобы гарантировать, что два хвостовых подруливающих устройства отслеживают опорное значение , , , , , .
2.3. Установленное предотвращение препятствий
Понятно, что такие задачи, как следование по пути и уклонение от препятствий, не обязательно совместимы.Если где-то на пути есть препятствие, USR должен либо отклониться от пути, либо столкнуться. Поэтому мы предлагаем переключаемую систему управления со следованием по пути и режимом обхода препятствий. Режим работы по умолчанию, который активен до тех пор, пока не приведет к столкновению, — это следование по пути. Когда USR приближается к препятствию и следование по пути еще больше уменьшает это расстояние, система переключается в режим предотвращения столкновений.
Переключаемая система наведения основана на последних результатах в области управления на основе наборов (Moe et al., 2016). Здесь широко используемая структура кинематического управления расширена для обработки задач на основе наборов, которые имеют допустимый интервал значений, а не точное желаемое состояние. Обход препятствия можно охарактеризовать как такую задачу, при которой расстояние между USR и препятствием должно сохраняться в пределах определенного интервала. В частности, допустимый интервал задается всеми положительными числами выше нижней границы R s . Однако подход, предложенный Moe et al. (2016) применимо к избыточным системам для одновременного выполнения нескольких совместимых задач.Поскольку две цели управления, т. Е. Следование траектории и уклонение от препятствий, несовместимы, мы изменили подход в соответствии с Moe and Pettersen (2016) и Kohl et al. (2017) для переключения между двумя задачами, т. Е. Двумя законами наведения θ ref, pf и θ ref, oa , описанными в разделе 2.2.
Для коммутируемой системы мы вводим дополнительный круг, который также закреплен в центре препятствия p o , с радиусом R м > R s .Радиус R м упоминается как радиус изменения моды . За пределами радиуса изменения режима система навигации всегда находится в режиме следования по траектории. Внутри R м может быть активен любой режим. Если режим следования по пути не приведет к дальнейшему уменьшению расстояния между USR и препятствием, он активен. В противном случае активируется уклонение от препятствий, и USR должен сходиться к безопасному радиусу R s . Радиус смены режима должен быть выбран достаточно большим, чтобы в случае переключения в режим обхода препятствий, USR сходился к безопасному радиусу без перерегулирования.Частично это достигается за счет настройки закона наведения при уклонении от препятствий таким образом, что USR сходится к смещению за пределами R s , а не к фактическому безопасному радиусу, как описано в предыдущем разделе. Желаемое поведение переключения фиксируется алгоритмом 1, который основан на теории множеств, описанной в Moe et al. (2016), Мо и Петтерсен (2016) и Коль и др. (2017).
Замечание 2 . Обратите внимание, что аналогичный подход применяется в Kohl et al.(2017) для уклонения от препятствий роботов-змей без двигателей, которые могут двигаться вперед только волнообразными шагами. Из-за колебательного поведения роботов-плавающих змей подход на основе наборов должен быть более консервативным, чтобы гарантировать, что никакая часть робота не столкнется с препятствием. В этой статье мы используем тот факт, что двигатели с подруливающим движением обеспечивают движение вперед, а шарниры управляют направлением движения, позволяя роботу безопасно огибать препятствие .
Алгоритм 1: Переключаемый алгоритм наведения на основе набора.
Для описанного выше сценария уклонения от препятствий задача σ по уклонению от препятствий определяется как расстояние между USR CM и препятствием. Он имеет допустимый интервал D = [ R s , ∞), а входные параметры показаны на рисунке 4, где θ ref, pf — желаемый курс для следования по пути, а θ o — угловая координата препятствия.Таким образом, как показано на рисунке 4, следование по траектории приведет к увеличению расстояния между USR и препятствием, когда угол между θ ref, pf и θ o меньше π / 2. В этом случае движение по траектории активно также в радиусе R м . Обратите внимание, что при использовании CM USR при вычислении σ, часть USR фактически разрешена в пределах безопасного радиуса R s . Это необходимо учитывать, выбирая достаточно большой R s .Кроме того, стратегия переключения в алгоритме 1 является полностью общей и может применяться для любой комбинации законов наведения для достижения альтернативного желаемого поведения, такого как отслеживание цели, отслеживание траектории или другие схемы следования по пути.
Рисунок 4 . Параметры уклонения от препятствий: основанная на множестве задача σ определяется как расстояние между центром препятствия и USR. За пределами радиуса изменения режима R м система всегда находится в режиме следования по траектории.Требуемый прямой путь лежит по оси x. Желаемый курс для следования по пути определяется как θ ref, pf и указывается черными стрелками для нескольких положений и ориентаций USR. Внутри R м система находится в режиме следования по траектории, если это приведет к увеличению σ, т. Е. Когда угол между θ ref, pf и θ o меньше или равен π / 2. В противном случае активен режим уклонения от препятствий, и в этом случае желаемый курс определяется θ ref, oa , и USR должен сходиться и отслеживать безопасный радиус R s .
Замечание 3 . Обратите внимание, что этот метод действителен для нескольких препятствий, при условии, что указанные препятствия не перекрываются и не перемещаются. В этих экспериментах использовалось только одно неподвижное препятствие из-за ограниченного размера испытательного бассейна. Обработка перекрывающихся и движущихся препятствий — тема будущей работы .
2,4. Обнаружение препятствий
В этой статье мы предполагаем, что USR должен работать в некоторой структурированной среде, на которую мы можем влиять, например.г., подводное нефтегазовое сооружение. Следовательно, мы предполагаем, что потенциальные препятствия отмечены какой-то геометрической формой, которую можно обнаружить с помощью камеры на головке USR и компьютерного зрения. Таким образом, препятствия разного размера могут быть отмечены разной формой. Для непредвиденных событий, таких как обломки, должна применяться другая схема обнаружения. Однако обратите внимание, что подход, основанный на наборах, все еще применим для уклонения с учетом оценки положения и скорости препятствия.
Для этих экспериментов мы использовали модель камеры-обскуры (Medioni and Kang, 2004), чтобы вывести уравнения, применяемые в реализованном алгоритме обнаружения.Три геометрические фигуры с известной площадью A r были построены с использованием световозвращающей ленты, и они представляют собой препятствия в экспериментах: круг, треугольник и квадрат (см. Рисунок 5). Чтобы избежать препятствия, объезжая его, как описано в разделах 2.2 и 2.3, положение препятствия в мировой системе координат p o должно быть известно. Следовательно, цель алгоритма обнаружения препятствий — вычислить это положение.
Рисунок 5 .Робот Мамба с подруливающими устройствами и светоотражающими маркерами, изображающими препятствия.
Алгоритм обнаружения препятствий основан на четырех основных шагах, которые показаны на рисунке 6: (1) Распознать и классифицировать маркер препятствия как треугольник, квадрат или круг, (2) найти положение и площадь маркера на изображении. x p , y p и A p , (3) сравните A p с фактической площадью маркера A r и используйте фокусное расстояние камеры f и положение маркера на изображении для расчета положения трехмерного препятствия относительно камеры poc, и (4) найти положение препятствия относительно мировой системы координат p o путем вращения и перемещения вокруг кадра камеры. ориентация и положение.Подробную реализацию можно найти в алгоритме 2.
Рисунок 6 . 3D-положение маркера относительно системы координат камеры poc = [xr, yr, zr] T может быть вычислено с использованием фокусного расстояния f камеры, площади маркера на изображении A P и реальность A r и положение маркера в системе координат изображения ( x p , y p ). В этой статье USR движется в плоскости, поэтому вертикальную составляющую y r можно не учитывать. (A) Преобразование входного изображения в черно-белое. (B) Найдите замкнутые границы, сгладьте их, вычислите кривизну и подсчитайте количество выступов для классификации геометрической формы. (C) Найдите положение ( x p , y p ) и площадь формы A p в системе координат изображения. (D) Используйте модель камеры-обскуры, фокусное расстояние камеры f и фактическую площадь формы A r для вычисления трехмерного положения обнаруженной формы относительно кадра координат камеры. (E) Расчетное положение обозначается как poc = [xr, yr, zr]. (F) Используйте положение и ориентацию камеры USR для вычисления обнаруженного положения в мировой системе координат p o .
Замечание 4 . Обратите внимание, что уравнения на рисунке 6D основаны на предположении, что маркер препятствия ориентирован параллельно плоскости системы координат xy камеры, то есть, что все углы треугольника имеют одинаковую координату z .Это предположение не выполняется, если камера смотрит на маркер под углом. Однако из-за относительно небольшого размера маркеров разность потенциалов в координате z углов ограничена и мала по сравнению с расстоянием, на котором необходимо наблюдать за ними, чтобы успешно избежать препятствия. Таким образом, это предположение является допустимым приближением и приведет к ограниченной ошибке в вычисленном положении .
3. Результаты экспериментов
В этом разделе мы обсуждаем полученные экспериментальные результаты для предложенной стратегии управления траекторией (раздел 3.1) и концепции обнаружения и уклонения от препятствий (разделы 3.2–3.3), описанной в предыдущем разделе, с использованием управляемой USR Mamba.
3.1. Прямой путь после
Во всех экспериментах углы шарниров робота были установлены равными нулю, тогда как начальная ориентация, θ (0), положение ЦМ робота по оси y , p y , пропорциональное усиление управления, k p , расстояние просмотра вперед, Δ, и управляющий вход для двигателей, u c , отображаются в таблице 2 для каждого испытания.Средняя потребляемая мощность рассчитывается с использованием следующего выражения
, где В, = 35 [В] и I avg [A] — средний ток, измеренный с помощью высокопроизводительного промышленного каротажного мультиметра FLUKE 289. Кроме того, была рассчитана средняя скорость поступательного движения для каждого экспериментального испытания. как
ῡ = ((pstop, x-pstart, x) 2+ (pstop, y-pstart, y) 2) / (tstop-tstart), (5), где p start и p stop представляют начальную и конечную точки пройденного расстояния в интервале времени t stop — t start .Усиление управления k d было установлено равным нулю для экспериментальных результатов, представленных для прямолинейного пути после подхода управления. Кроме того, смещение шарнира ϕ 0 было насыщено на ± 20 °, чтобы гарантировать, что физическое ограничение углов шарнира робота не будет превышено.
Таблица 2 . Средняя скорость поступательного движения и потребляемая мощность для пути после тематических исследований с использованием подводного робота-змеи мамба с подруливающими устройствами.
Предыдущие экспериментальные результаты следования по траектории подводных роботов-змей с использованием волнистости тела как для движения, так и для управления направлением показали, что робот может достигать и следовать по пути, используя закон наведения LOS (Kelasidi et al., 2016a, 2017b). Однако использование колебательной модели походки вызывает установившиеся колебания около нуля для ошибки поперечного сечения и ориентации, что ожидается, поскольку трудно добиться чисто не колебательного движения для CM и ориентации подводной плавающей змеи. роботы (Kelasidi et al., 2016а, 2017б). Эти колебания могут быть ограничивающими для некоторых приложений в подводной среде, таких как, например, стыковка (Sans-Muntadas et al., 2017).
Экспериментальные результаты для четырех различных пробных траекторий Mamba с подруливающими устройствами представлены на рисунке 7, см. Также дополнительные видео. Как показано на рисунке 7, роботу удается сходиться и следовать по желаемому пути для всех исследованных случаев. Кроме того, эталонная ориентация отслеживается без колебаний.Перерегулирование и начальное быстрое изменение ориентации, показанное на рисунке 7, когда робот-змея приближается к траектории, является результатом настройки и, в частности, выбора расстояния просмотра вперед Δ. Чем больше выбор Δ, тем меньше будет перерегулирование и тем медленнее будет скорость сходимости. Таким образом, выбор Δ — это компромисс между сходимостью и выбросом (Kelasidi et al., 2017b). Небольшая погрешность в установившемся режиме при поперечной ошибке может быть результатом нескольких факторов, таких как возможное рассогласование двух подруливающих устройств, используемых в хвостовом модуле робота, ошибки измерения от различных датчиков, используемых во время экспериментов, и силы на роботе из-за использования троса.В будущем можно будет изучить более совершенные подходы к управлению курсом, чтобы устранить эту небольшую ошибку, например, путем включения комплексного действия (Caharija et al., 2012). В дополнение к сходимости к прямолинейному пути, мы получили результаты, касающиеся достигнутой скорости поступательного движения и потребляемой мощности для всех исследованных испытаний, и они показаны в Таблице 2. Достигнутая скорость очень похожа во всех испытаниях, что и ожидается. поскольку для всех исследованных случаев использовалось одно и то же значение управляющего входа для двигателей.Однако средняя потребляемая мощность варьируется для разных исследуемых трактов в соответствии с тематическими исследованиями, как показано в Таблице 2. Это разумно, поскольку потребляемая мощность относится не только к трастерам, но также и к объединенным модулям. Срабатывание регулятора направления и, следовательно, совместное движение для каждого испытания зависит от начального курса и расстояния от траектории, которое меняется в разных испытаниях.
Рисунок 7 . Путь экспериментальных результатов следующий. (A) Положение центра масс для u c = 60, k p = 1, k d = 0, Δ = 180 см и θ = — 82,7 o . (B) Положение центра масс для u c = 60, k p = 1, k d = 0, Δ = 90 см и θ = — 26,2 o . (C) Положение центра масс для u c = 60, k p = 1, k d = 0, Δ = 90 см и θ = 21 .4 или . (D) Положение центра масс для u c = 60, k p = 1, k d = 0, Δ = 130 см и θ = 2,7 или . (E) Ориентация робота для кейса (A). (F) Ориентация робота для кейса (B). (G) Ориентация робота для кейса (C). (H) Ориентация робота для кейса (D).(I) Движение подводного робота-змеи Мамба с подруливающими устройствами во время следования по пути для экспериментальных результатов, представленных в (C, G) , где красная линия указывает опорный путь.
3.2. Обнаружение препятствий
Для экспериментов, представленных в этой статье, алгоритм обнаружения препятствий был запущен в автономном режиме, а обнаруженная позиция была добавлена вручную в переключаемую систему наведения и управления, описанную в разделе 2.3. Тем не менее, алгоритм также может быть полностью автономным как часть онлайн-системы управления; алгоритм обнаружения достаточно быстр, поэтому время выполнения не будет проблемой при онлайн-реализации.Внедрение необходимой структуры коммуникации и контроля, необходимой для достижения этой цели, является темой будущей работы. Однако в представленных результатах алгоритм обнаружения препятствий был запущен, и обнаруженная позиция добавлена в систему управления за одну операцию без удаления робота из пула или его выключения.
Для определения положения препятствия алгоритм обнаружения, описанный на рисунке 6, был запущен три раза для разных положений и ориентации камеры, см. Рисунки 8, 9A.Обратите внимание, что при тестировании схемы обнаружения препятствий доступные положения и ориентации USR, где маркер препятствия находился в кадре камеры, были ограничены размером пула и системой слежения Qualisys. Среднее из трех обнаруженных положений p o затем вводилось в систему управления и использовалось для оставшейся части экспериментов. Чтобы количественно оценить точность алгоритма, фактическое положение препятствия было измерено с помощью системы слежения Qualisys, и окончательное обнаруженное положение p o было приблизительно равно 0.07 м от фактического положения препятствия, что соответствует 7% безопасного радиуса R s = 1 м и 3,9% от общей длины робота. Этот результат достаточно точен для безопасного использования в схеме уклонения от препятствий, тем самым подтверждая, что предложенный подход к обнаружению весьма применим. Обратите внимание, что для достижения достаточно хорошей визуализации для обнаружения и классификации отражающих маркеров и для максимально точного моделирования подводной среды, все огни были выключены во время экспериментов, за исключением источников света на камере USR и трекинга Qualisys. система.
Алгоритм 2: Алгоритм обнаружения препятствий.
Рисунок 8 . Алгоритм обнаружения препятствий, описанный на рисунке 6, был запущен три раза для разных положений и ориентации USR, показанных пурпурным, синим и красным соответственно. Для двух последних случаев алгоритм также обнаруживает искаженное поверхностное отражение маркеров и классифицирует его как квадрат и треугольник соответственно. Для настоящих подводных приложений этого явления не будет, и эти ложные обнаружения легко игнорировать, наблюдая, что их координата y отрицательна, т.е.е., они находятся над поверхностью. (A) Среднее обнаруженное положение ♢ находилось на расстоянии 7 см от фактического положения препятствия ○. (B) Обнаруженное положение препятствия относительно камеры, соответствующее пурпурному цвету в (A). (C) Положение обнаруженного препятствия относительно камеры, соответствующее синему цвету в (A). (D) Положение обнаруженного препятствия относительно камеры, соответствующее красному цвету в (A) .
Рисунок 9 .Экспериментальные результаты следования по пути с обнаруженным положением препятствия и объезд препятствия. (A) Алгоритм обнаружения препятствий, описанный на рисунке 6, был запущен три раза для разных положений и ориентации USR. Среднее обнаруженное положение ♢ было приблизительно 0,07 м от фактического положения препятствия ○. (B) Путь USR следует по пути (синий), переключается на уклонение от препятствий и обходит обнаруженное препятствие (зеленый) и, наконец, переключается обратно на следование по пути (синий). (C) Фактическая и желаемая ориентация робота. Система управления переключается со следования по траектории на уклонение от препятствий при ≈ t = 13 с и обратно при ≈ t = 37 с. (D) Движение подводной змеи Мамба с подруливающими устройствами во время экспериментов по обнаружению и уклонению от препятствий. Соответствующие позиции указаны в (B) .
3.3. Избегание препятствий
Экспериментальная установка для следования по траектории и избегания препятствий идентична той, что описана в предыдущем разделе, а результаты экспериментов показаны на рисунках 9B – D.Запись эксперимента можно увидеть в дополнительных видео. Исходное положение USR находится на опорном пути, а начальный режим — следование пути. Как только USR входит в радиус изменения режима R м = 3 м, очевидно, что продолжение следования по траектории приведет к приближению USR к препятствию. Следовательно, активируется уклонение от препятствия, и робот обходит препятствие, поворачиваясь и пытаясь оставаться за пределами безопасного радиуса R s = 1 м.Согласно теории, описанной в разделе 2.2, USR сходится к постоянному смещению безопасного радиуса, которое может быть уменьшено за счет другого выбора коэффициентов усиления. Однако для этого приложения очень важно избегать перерегулирования до R s , и, таким образом, предпочтительнее большее смещение. Кроме того, положение USR определяется CM, что также требует более консервативного подхода, поскольку части USR фактически будет разрешено входить в безопасный радиус R s и должна быть такая возможность. безопасно.Наконец, физическое препятствие в бассейне частично заблокировало систему слежения за камерой, что сделало невозможным с доступной экспериментальной установкой попытаться использовать менее консервативные подходы, которые лучше использовали бы гибкость USR. Обратите внимание, что робот обходит препятствие, выбирая направление по окружности, обеспечивающее кратчайший путь, как описано в разделе 2.2.
Когда USR преодолевает препятствие, следование по траектории снова гарантирует, что робот уйдет от препятствия.Затем снова активируется следование по пути, и робот снова сходится на путь. Это можно увидеть на Рисунке 9B. На рис. 9С показана исходная ориентация, обеспечиваемая переключаемой системой наведения, и фактическая ориентация USR. Реализованный PD-контроллер обеспечивает достаточно точное отслеживание эталона. Обратите внимание, что переключаемая система наведения, описанная в алгоритме 1, приводит к резким изменениям исходной ориентации, когда система переключается между следованием по траектории и избеганием препятствий.Чтобы обеспечить систему управления допустимым опорным сигналом, реализована функция гиперболического сглаживания, обеспечивающая непрерывный опорный сигнал после переключения (Kohl et al., 2017). Кроме того, заданное совместное смещение ϕ 0 фильтруется фильтром нижних частот первого порядка перед тем, как поступить в контроллер нижнего уровня.
На рис. 9D показаны изображения эксперимента. USR явно преодолевает препятствие на круговой траектории, прежде чем вернуться к исходной траектории.Выбранные параметры управления для реализации следующие:
1. Траектория в соответствии с законом наведения θ ref, pf : k tran = 0,1, k вдоль = 0,15 (соответствует дальности обзора Δ = 1,5 м)
2. Закон наведения при уклонении от препятствий θ ref, oa : k tran = 0,02, k вдоль = 0,15
3. Контроллер ϕ o : k p = 0.42, к d = 0,03
4. Функция сглаживания:
α (t, tlast switch) = 12 (tanh (α1 (t-tlast switch-α2) +1)), α1 = 1,2, α2 = 1,64. Выводы
USRобладают множеством основных качеств для автономных подводных операций, таких как эффективное передвижение, гибкие тела и возможность выполнять задачи вмешательства. Эти универсальные роботы могут быть оснащены различными модулями, такими как подруливающие устройства или стабилизаторы, и применимы для решения множества задач в нескольких областях исследований.
В этой статье мы представляем систему наведения и управления для обеспечения следования по траектории и избегания препятствий для USR с подруливающими устройствами, в дополнение к алгоритму компьютерного зрения для обнаружения и расчета положения потенциальных препятствий. Основываясь на предварительных результатах для обеспечения энергоэффективного движения и высокой скорости, движение USR основано на подруливающих устройствах для движения вперед, тогда как управление направлением достигается за счет суставов тела. Все предложенные методы впервые проверены экспериментально, впервые с использованием надводного USR Mamba.Дальнейшая работа включает расширение предлагаемого подхода к наведению и управлению до 3D, чтобы иметь возможность исследовать следование по траектории и уклонение от препятствий USR с помощью двигателей подруливающих устройств в 3D.
Авторские взносы
Все перечисленные авторы внесли существенный, прямой и интеллектуальный вклад в работу и одобрили ее к публикации.
Заявление о конфликте интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Благодарности
Эта работа финансировалась Исследовательским советом Норвегии через схему финансирования Центров передового опыта, проект №. 223254-NTNU AMOS и VISTA — программа фундаментальных исследований в сотрудничестве между Норвежской академией наук и литературы и Statoil.
Дополнительные материалы
Дополнительные материалы к этой статье можно найти в Интернете по адресу: https://www.frontiersin.org/articles/10.3389/frobt.2019.00057/full#supplementary-material
Дополнительное видео 1. Избегание препятствий.
Дополнительное видео 2. Путь следования за Мамбой.
Список литературы
Аламир М., Эль Рафей М., Хафиди Г., Маршанд Н., Порез М. и Бойер Ф. (2007). «Дизайн обратной связи для трехмерного движения робота, похожего на угря,» в Proceedings of the IEEE International Conference on Robotics and Automation (Roma), 256–261.
Google Scholar
Бхатти, А. (ред.). (2008). Стерео Видение .Вена: InTech Open.
Google Scholar
Бонин-Фонт, Ф., Ортис, А., Оливер, Г. (2008). Визуальная навигация для мобильных роботов: обзор. J. Intell. Робот. Syst. 53: 263. DOI: 10.1007 / s10846-008-9235-4
CrossRef Полный текст | Google Scholar
Børhaug, E., and Pettersen, K. Y. (2006). «Траектория прямой видимости для подводных аппаратов с неразорвавшимися механизмами», в Труды 7-й конференции МФБ по маневрированию и управлению морскими судами (Лиссабон).
Бусаид А., Теодоридис Т. и Нефти-Мезиани С. (2016). «Представление новой геометрической модели на основе маркеров в монокулярном зрении», 2016 13-й семинар по позиционированию, навигации и коммуникациям (WPNC) (Бремен), 1–6.
Google Scholar
Брейвик М., Фоссен Т. И. (2008). «Руководящие законы для управления движением в плоскости», в материалах Proceedings of the 47th IEEE Conference on Decision and Control (Мексика), 570–577.
Google Scholar
Caharija, W., Петтерсен, К. Ю., Гравдал, Дж. Т., и Бёрхауг, Э. (2012). «Интегральное наведение LOS для горизонтального следования по траектории неработающих автономных подводных аппаратов в присутствии вертикальных океанских течений», в протоколе Proceedings of the American Control Conference (Montreal, QC), 5427–5434.
Google Scholar
Крист, Р. Д., и Вернли, Р. Л. (2013). Руководство ROV: Руководство пользователя для дистанционно управляемых транспортных средств . Уолтем, Массачусетс: Elsevier Science.
Google Scholar
Креспи, А., Бадерчер А., Гиньяр А. и Эйспеерт А. (2005). «Плавание и ползание с роботом-амфибией-змеей», в Труды Международной конференции IEEE по робототехнике и автоматизации (ICRA), (Барселона), 3024–3028.
Google Scholar
Crespi, A., and Ijspeert, A.J. (2006). «AmphiBot II: робот-амфибия-змея, который ползает и плавает с помощью центрального генератора шаблонов», в материалах Труды 9-й Международной конференции по альпинистским и шагающим роботам (CLAWAR) (Брюссель), 19–27.
Google Scholar
Фоссен, Т. И. (2011). Справочник по гидродинамике и управлению движением морских судов . Вайли.
Google Scholar
Фокс Д., Бургард В. и Трун С. (1997). Подход динамического окна к предотвращению столкновений. Робот IEEE. Автомат. Mag. 4, 23–33. DOI: 10.1109 / 100.580977
CrossRef Полный текст | Google Scholar
Голдберг, С. Б., Маймон, М. В., и Маттис, Л. (2002). «Стереовидение и программное обеспечение для навигации марсохода для исследования планет», в Proceedings of the IEEE Aerospace Conference Proceedings (Big Sky, MT), 5.
Google Scholar
Эрнандес, Э., Каррерас, М., Ридао, П. (2015). Сравнение алгоритмов планирования гомотопических путей для робототехнических приложений. Робот. Auton. Syst. 64, 44–58. DOI: 10.1016 / j.robot.2014.10.021
CrossRef Полный текст | Google Scholar
Келасиди, Э., Коль, А. М., Петтерсен, К. Ю., и Гравдаль, Дж. Т. (2017a). «Экспериментальное исследование следования по траектории подводного робота-змеи с хвостовым плавником», Труды 20-го Всемирного конгресса Международной федерации автоматического управления (Тулуза), 11182–11190.
Google Scholar
Келасиди, Э., Лильебек, П., Петтерсен, К. Ю., и Гравдаль, Дж. Т. (2016a). Инновация в подводных роботах: роботы-плавающие змеи, вдохновленные биологией. Робот IEEE. Автомат. Mag. 23, 44–62. DOI: 10.1109 / MRA.2015.2506121
CrossRef Полный текст | Google Scholar
Келасиди, Э., Лильебек, П., Петтерсен, К. Ю., и Гравдаль, Дж. Т. (2017b). Интегральное наведение по линии прямой видимости для управления подводными роботами-змеями по траектории: теория и эксперименты. IEEE Trans. Робот. 33, 1–19. DOI: 10.1109 / TRO.2017.2651119
CrossRef Полный текст | Google Scholar
Келасиди, Э., Петтерсен, К. Ю., Гравдал, Дж. Т. (2015). «Энергоэффективность подводных роботов», в Труды 10-й конференции МФБ по маневрированию и управлению морскими судами (Копенгаген), 152–159.
Google Scholar
Келасиди, Э., Петтерсен, К. Ю., Лильебек, П., и Гравдаль, Дж. Т. (2016b). «Эффективность передвижения подводных роботов-змей с двигателями», в Proceedings of the IEEE International Symposium on Safety, Security and Rescue Robotics, (Lausanne), 174–181.
Google Scholar
Хатиб О. (1985). «Предотвращение препятствий в реальном времени для манипуляторов и мобильных роботов», в материалах Proceedings of the IEEE International Conference on Robotics and Automation (St. Louis, MO), 500–505.
Google Scholar
Коль, А., Мо, С., Келасиди, Э., Петтерсен, К. Ю., и Гравдаль, Дж. Т. (2017). «Установленное отслеживание пути и избегание препятствий для подводных роботов-змей», в Международная конференция IEEE по робототехнике и биомиметике (Макао), 1206–1213.
Google Scholar
Коль, А. М., Келасиди, Э., Мохаммади, А., Маджоре, М., и Петтерсен, К. Ю. (2016). Планарное управление маневрированием подводных роботов-змей с использованием виртуальных голономных ограничений. Bioinspir. Биомимет. 11: 065005. DOI: 10.1088 / 1748-3190 / 11/6/065005
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Корен Ю. и Боренштейн Дж. (1991). «Методы потенциального поля и присущие им ограничения для навигации мобильных роботов», в Proceedings of the IEEE International Conference on Robotics and Automation (Sacramento, CA), 1398–1404.
Google Scholar
Кувата Ю., Вольф М. Т., Заржицкий Д. и Хантсбергер Т. Л. (2014). Безопасная морская автономная навигация с COLREGS с использованием скоростных препятствий. IEEE J. Ocean. Англ. 39, 110–119. DOI: 10.1109 / JOE.2013.2254214
CrossRef Полный текст | Google Scholar
Lapierre, L., и Jouvencel, B. (2005). «Контроль следования по траектории для робота, похожего на угря», в Proceedings of the MTS / IEEE International Conference Oceans (Brest), 460–465.
Google Scholar
Лаубах, С. Л., и Бурдик, Дж. У. (1999). «Автономный планировщик пути на основе датчиков для планетарных микропереходов», в материалах Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Detroit, MI), Vol. 1, 347–354.
Google Scholar
Лей, Г., Чжитао, X., Цзюнь, В., Фанг, З., и Цзинхун, М. (2013). Метод измерения дальности монокулярного зрения, основанный на компенсации динамической ошибки. Внутр. J. Digit.Content Technol. Прил. 7, 230–237. DOI: 10.4156 / jdcta.vol7.issue5.28
CrossRef Полный текст | Google Scholar
Ли, Б., Ю, С., Ма, С., и Ван, Ю. (2011). «Робот-амфибия, похожий на змею, с необычной походкой на земле и в воде», в материалах Proceedings of the IASTED International Conference Intelligent Systems and Control (ISC 2011) (Calgary, AB), 100–105.
Google Scholar
Лайтхилл, М. Дж. (1970). Тяга для водных животных с высокой гидромеханической эффективностью. J. Fluid Mech. 44, 265–301. DOI: 10.1017 / S0022112070001830
CrossRef Полный текст | Google Scholar
Liljebäck, P., Stavdahl, Ø., Pettersen, K., and Gravdahl, J. (2014). «Мамба — водостойкий робот-змея с тактильным восприятием», Труды Международной конференции по интеллектуальным роботам и системам (Чикаго, Иллинойс), 294–301.
Loe, Ø. А. Г. (2008). Предотвращение столкновений беспилотных наземных транспортных средств . (Дипломная работа).Тронхейм: Норвежский университет науки и технологий.
Google Scholar
Маллиос А., Ридао П., Рибас Д., Каррерас М. и Камилли Р. (2016). К автономной разведке в замкнутых подводных средах. J. Полевой робот. 33, 994–1012. DOI: 10.1002 / rob.21640
CrossRef Полный текст | Google Scholar
McIsaac, K., and Ostrowski, J. (2002). «Эксперименты по управлению с обратной связью для подводного робота, похожего на угря», в Proceedings of the IEEE International Conference on Robotics and Automation (ICRA) (Washington, DC), 750–755.
Google Scholar
McIsaac, K., and Ostrowski, J. (2003). Планирование движения для угловатой локомоции. IEEE Trans. Робот. Автомат. 19, 637–625. DOI: 10.1109 / TRA.2003.814495
CrossRef Полный текст | Google Scholar
Mclsaac, K., and Ostrowski, J. (1999). «Геометрический подход к косоугольному передвижению: моделирование подводного робота-угря», в материалах Proceedings of the International Conference on Robotics and Automation (ICRA) (Detroit, MI), 2843–2848.
Медиони, Г., и Канг, С. Б. (2004). Новые темы компьютерного зрения . Река Аппер Сэдл, Нью-Джерси: Prentice Hall PTR.
Google Scholar
Мо, С., Антонелли, Г., Тил, А. Р., Петтерсен, К. Ю., и Шримпф, Дж. (2016). Задачи на основе наборов в рамках устойчивой к сингулярности многозадачности обратной кинематики: общая формулировка, анализ устойчивости и экспериментальные результаты. Фронт. Робот. AI 3:16. DOI: 10.3389 / frobt.2016.00016
CrossRef Полный текст | Google Scholar
Мо, С., Петтерсен, К. Ю. (2016). «Установленный путь прямой видимости (LOS), отслеживающий с предотвращением столкновений для необитаемых беспилотных надводных судов», в Труды 24-й Средиземноморской конференции по управлению и автоматизации (Афины), 402–409.
Google Scholar
Николсон, Дж. У., и Хили, А. Дж. (2008). Современное состояние приложений и технологий автономных подводных аппаратов (АНПА). Mar. Technol. Soc. J. 42, 44–51. DOI: 10.4031 / 002533208786861272
CrossRef Полный текст | Google Scholar
QUA (2018). Qualisys – Системы захвата движения . Доступно в Интернете по адресу: http://www.qualisys.com/ (по состоянию на 25 сентября 2018 г.).
Ридао, П., Каррерас, М., Рибас, Д., Санс, П., и Оливер, Г. (2014). «Вмешательство АНПА: следующая проблема», в материалах Протокола 19-го Всемирного конгресса МФБ, (Кейптаун), 12146–12159.
Google Scholar
Санс-Мунтадас, А., Келасиди, Э., Петтерсен, К. Ю., Брекке, Э. (2017). «Планирование спирального пути для стыковки автомобилей без гидроусилителя с ограниченным полем обзора», в материалах Proceedings of the 1st IEEE Conference on Control Technology and Applications (Hawaii), 732–739.
Google Scholar
Стефанини, К., Орофино, С., Манфреди, Л., Минчев, С., Маррацца, С., Ассаф, Т., и др. (2012). Новый автономный плавательный робот с биоинспекцией, разработанный нейробиологами и биоинженерами. Bioinspir.Биомимет. 7: 025001. DOI: 10.1088 / 1748-3182 / 7/2/025001
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Свердруп-Тайгесон, Дж., Келасиди, Э., Петтерсен, К. Ю., Гравдаль, Дж. Т. (2016a). «Структура управления для манипуляторов подводного плавания, оснащенных подруливающими устройствами, на основе биологических методов», в материалах Труды 10-й конференции IFAC по приложениям управления в морских системах, (Тронхейм), 89–96.
Google Scholar
Свердруп-Тайгесон, Дж., Келасиди, Э., Петтерсен, К. Ю., и Гравдаль, Дж. Т. (2016b). «Подводный плавательный манипулятор — био-вдохновленный auv», в Proceedings of the IEEE / OES Autonomous Underwater Vehicles (Tokyo), 387–395.
Google Scholar
Такаяма Т. и Хиросе С. (2002). «Амфибия с трехмерным активным шнуровым механизмом« спираль »со спиралевидным плаванием», в Труды Международной конференции IEEE / RSJ по интеллектуальным роботам и системам (IROS) (Лозанна), 775–780.
Google Scholar
ван ден Берг, Дж., Гай, С. Дж., Лин, М., и Маноча, Д. (2011). «Взаимное предотвращение столкновений n-тел», в Robotics Research: The 14th International Symposium ISRR (Берлин; Гейдельберг: Springer), 3–19.
Google Scholar
Уилбур К., Ворус В., Цао Ю. и Карри С. (2002). «Волнообразное транспортное средство на основе миноги», в Neurotechnology for Biomimetic Robots , ред. Дж. Эйерс, Дж. Л. Дэвис и А. Рудольф (Кембридж: Брэдфорд / MIT Press), 285–296.Доступно в Интернете по адресу: https://cbns.ucr.edu/faculty/currie_robolamprey2002.pdf
Google Scholar
Ямада, Х., Чигисаки, С., Мори, М., Такита, К., Огами, К., и Хиросе, С. (2005). «Разработка змееподобного робота-амфибии ACM-R5», в Труды 36-го Международного симпозиума по робототехнике (Токио).
Google Scholar
Динамическое предотвращение препятствий для квадрокоптеров с камерами событий
ВВЕДЕНИЕ
Микро-летательные аппараты (MAV) могут открыть новые рынки, потенциально стоящие несколько миллиардов долларов.Эти рынки включают в себя аэрофотосъемку [прогнозируемая стоимость в 4 миллиарда долларов к 2025 году ( 1 )], доставка на «последнюю милю» [90 миллиардов долларов к 2030 году ( 2 )] и воздушную мобильность [на сумму около 8 миллиардов долларов в 2030 году ( 3 ) )]. Хотя рыночный потенциал MAV является многообещающим, безопасность остается ключевой проблемой для MAV. В новостях сообщалось о нескольких авариях дронов, связанных либо с объектами, брошенными в квадрокоптеры во время общественных мероприятий ( 4 , 5 ), либо со столкновениями с птицами ( 6 , 7 ).Таким образом, возможность MAV уклоняться от быстро движущихся объектов (рис. 1) имеет решающее значение для развертывания безопасных летающих роботов в больших масштабах.
Рис. 1 Последовательность маневра уклонения.Временная задержка между восприятием и действием играет ключевую роль в избегании препятствий. Чем выше задержка, тем меньше времени робот должен реагировать и выполнять маневр уклонения ( 8 ). Это особенно важно для MAV, где столкновение может не только нанести ущерб окружающей среде, но и вызвать серьезный отказ оборудования.Кроме того, у микроквадрокоптеров снижена полезная нагрузка, что жестко ограничивает возможности датчиков и вычислительных ресурсов, которые они могут нести.
Существующая литература по предотвращению препятствий для MAV опирается на стандартные камеры [в монокуляре ( 9 — 11 ) или стерео ( 12 — 15 )] или на камерах глубины ( 16 — 18 ). Однако в этих работах предполагается, что препятствия в окружающей среде либо статические, либо квазистатические (т.е., медленное относительное движение). Точно так же современные потребительские дроны в настоящее время не способны надежно обнаруживать движущиеся препятствия и избегать их. Например, дрон Skydio, один из самых продвинутых автономных дронов на рынке на сегодняшний день, не способен справляться с движущимися объектами ( 19 ). Таким образом, разработка эффективных решений для предотвращения динамических препятствий является ключевой задачей в исследованиях робототехники, а также высоко ценится крупными игроками отрасли.
Чтобы избежать быстро движущихся препятствий, нам нужно быстро их распознавать.Для этой цели стандартные камеры не подходят, потому что у них средняя задержка в десятки миллисекунд (время экспозиции стандартной камеры варьируется от 1 до 100 мс). Следовательно, их ограничения проистекают из их физической природы и не могут быть решены с помощью сложных алгоритмов. Одним из решений может быть использование камер для событий; время реакции этих датчиков составляет микросекунды. Камеры событий ( 20 ) — это сенсоры с биоинспирированием, которые работают иначе, чем традиционные камеры. Вместо того, чтобы захватывать изображения с фиксированной скоростью, камера событий асинхронно измеряет попиксельные изменения яркости.Это приводит к потоку событий с разрешением в микросекунды.
В недавнем исследовании роли задержки восприятия для высокоскоростного распознавания и избегания ( 8 ) было аналитически показано, что с использованием камер событий задержка между моментом, когда датчик запускает визуальный сигнал и обрабатывает его. на вывод управляющих команд заметно меньше, чем у стандартных камер (микросекунды против десятков микросекунд). Эти результаты многообещающие для робототехники. Однако стандартные алгоритмы технического зрения не могут быть применены, потому что на выходе камеры событий являются не изображения, а поток асинхронных событий.Таким образом, необходимо разработать альтернативные алгоритмы, чтобы раскрыть весь потенциал камер событий для решения поставленной задачи.
Камера событий имеет интеллектуальные пиксели, которые запускают информацию независимо друг от друга: всякий раз, когда пиксель обнаруживает изменение интенсивности в сцене (например, вызванное относительным движением), этот пиксель запускает информацию в момент обнаружения изменения интенсивности. . Эта информация называется событием и кодирует время (с разрешением в микросекундах), в которое произошло событие, местоположение пикселя и знак изменения интенсивности.Пусть t k −1 будет последним моментом, когда событие сработало в местоположении пикселя x , и пусть L k −1 = L ( x , t k −1 ) уровень интенсивности в таком пикселе в момент времени t k −1 . Новое событие запускается в том же месте пикселя в момент времени t k , как только разница между интенсивностью L k −1 и L k больше, чем определенная пользователем порог C > 0.Другими словами, событие запускается, если ‖ L ( x , t k ) — L ( x , t k −1 ) ‖> C (положительное событие) или ‖ L ( x , t k ) — L ( x , t k −1 ) ‖ <- C (отрицательное событие ). Мы отсылаем читателя к ( 21 ) для получения дополнительной информации. Чтобы лучше понять, что происходит со всем датчиком, мы сравниваем выходной сигнал камеры событий с выходом обычной камеры на рис.2 и на видео ( 22 ).
Рис. 2 Сравнение выходного сигнала обычной камеры и событийной камеры для вращающегося диска с черной точкой.Обычная камера снимает кадры с фиксированной скоростью; камера событий выводит только знак изменения яркости непрерывно в виде спирали событий в пространстве-времени (красный цвет — положительные изменения; синий — отрицательные изменения).
Камеры событий можно рассматривать как асинхронные датчики, активируемые движением, поскольку они обеспечивают измерения только в том случае, если и где есть относительное движение между камерой и окружающей средой.Кроме того, поскольку их задержка составляет порядка микросекунд, они являются естественным выбором для обнаружения и избегания быстро движущихся препятствий с помощью летающих MAV. Если удалить события, вызванные эго-движением транспортного средства ( 23 , 24 ), можно напрямую получить информацию о движущейся части сцены. Это дает множество преимуществ по сравнению со стандартными камерами для обнаружения динамических препятствий: (i) результат меньше и легче кадра и, следовательно, дешевле в обработке; (ii) сегментация между статическими и динамическими объектами не требуется, поскольку для этого можно использовать временную статистику каждого события; (iii) их высокое временное разрешение (порядка микросекунд) позволяет выполнять зондирование с малой задержкой.
В последние годы камеры для событий вызвали интерес сообщества робототехники ( 21 ). Обнаружение препятствий является одним из приложений с наибольшим потенциалом, и в предыдущих работах исследовалось использование этих датчиков для обнаружения столкновений ( 25 ) и отслеживания объектов ( 23 , 26 ). Однако в литературе доступно очень мало примеров управления с обратной связью на основе камер событий. Среди них большинство работ сосредоточено на простых задачах с низкой размерностью, таких как регулировка заголовка с 1 степенью свободы (DoF) ( 27 , 28 ), управление взглядом стереокамеры ( 29 , 30 ), балансировка полюсов с 2 степенями свободы ( 31 ), роботизированное вратарское управление с 1 степенями свободы ( 32 , 33 ) или управление наземными роботами среди статических препятствий ( 34 — 36 ).
Недавно мы сообщали о замкнутом контуре управления более сложными роботизированными системами, такими как квадрокоптеры, с использованием камер событий ( 37 — 39 ). В ( 37 ) мы предложили основанный на событиях алгоритм визуально-инерциальной одометрии (VIO) для оценки состояния и отслеживания траектории квадрокоптера с обратной связью. Вместо этого ( 38 ) и ( 39 ) больше всего связаны с этой статьей. В ( 38 ) мы проанализировали возможность обнаружения сферических объектов, брошенных в стационарную камеру событий, на небольших встроенных процессорах для квадрокоптеров.В ( 39 ) мы показали предварительные результаты использования неглубоких нейронных сетей для выделения движущихся объектов из потоков событий и продемонстрировали приложение для обхода препятствий квадрокоптерам. Однако результирующая задержка распознавания составила 60 мс, а не 3,5 мс, как указано в этой статье, что сильно ограничивает максимальную относительную скорость, с которой можно было уклониться от движущихся объектов. Кроме того, в отличие от этой статьи, мы не учитывали относительное расстояние и скорость для вычисления команд уклонения.В данной работе реализовано и продемонстрировано динамическое уклонение от препятствий с малой задержкой (3,5 мс) на автономном квадрокоптере с относительной скоростью до 10 м / с.
Наш алгоритм обнаружения движущихся препятствий работает, собирая события в течение короткого скользящего окна и компенсируя движение робота в этом временном окне. На рисунке 3 показаны эффекты компенсации движения эго: слева трехмерный (3D) объем событий, накопленных в течение произвольного временного окна 10 мс, а справа те же события после того, как эго -компенсация движения, обратная проекция на плоскость изображения.Мы проанализировали временную статистику событий с компенсацией движения, чтобы удалить те, которые генерируются статической частью среды.
Рис. 3 Эффекты компенсации движения эго.Наш алгоритм собирает все события, которые произошли за последние 10 мс, представленные здесь в трехмерном объеме (слева), и использует IMU для компенсации движения камеры. Таким образом, события с компенсацией эго-движения проецируются в общий кадр изображения (правая сторона), где каждый пиксель (pxl) содержит потенциально несколько событий.Анализируя временную статистику всех событий, проецируемых на каждый пиксель, наш подход позволяет различать пиксели, принадлежащие статической части сцены и движущимся объектам.
Вообще говоря, наш алгоритм основан на интуиции, что статическая часть сцены запускает события равномерно во всем временном окне, и после компенсации эго-движения пиксели, принадлежащие статическим объектам, показывают равномерное распределение временных меток; И наоборот, динамические объекты генерируют компенсированные движением эго события, которые накапливаются вокруг определенных участков временного окна и, следовательно, могут быть различимы.Наша методика обнаружения движущихся препятствий с помощью камер событий основана на методе, предложенном в ( 23 ), где авторы использовали основанную на оптимизации схему компенсации движения эго. Мы изменили этот метод, чтобы полагаться только на инерциальный измерительный блок (IMU) для компенсации движения эго, без использования какой-либо схемы оптимизации, что делает алгоритм достаточно быстрым для работы в реальном времени на небольшом бортовом компьютере.
Анализ влияния игнорирования линейного компонента эго-движения робота и интуитивное объяснение того, как и почему работает наш алгоритм, представлены в дополнительных материалах.Подробное объяснение компенсации событий движением эго — что позволило нам получить так называемую рамку событий, содержащую только события, исходящие от движущихся объектов, с очень высокой скоростью — объясняется в Материалах и методах. Мы использовали алгоритм быстрой кластеризации, чтобы различать различные объекты в кадре события, и использовали фильтр Калмана для получения информации об их скорости. На рисунке 4 представлено наглядное объяснение шагов, задействованных в нашем алгоритме, которые более подробно описаны в разделе «Материалы и методы».
Рис. 4 Этапы алгоритма компенсации эго-движения для выделения событий, относящихся к движущимся препятствиям.( A ) Кадр, сделанный камерой Insightness SEES1, демонстрирующий размытие при движении из-за относительного движения между датчиком и движущимся препятствием. ( B ) Все события накапливаются в последнем окне, причем красный и синий цвета указывают полярность (положительная и отрицательная соответственно). ( C ) Результат компенсации эго-движения, отображающий белым цветом все пиксели, в которых произошло хотя бы одно событие во временном окне.( D ) События с компенсацией движения с цветовым кодом, представляющим нормированную среднюю отметку времени: события, принадлежащие динамической части сцены, представлены желтым цветом. ( E ) Среднее изображение отметки времени после установки порога: зеленый и фиолетовый цвета указывают на неподвижную и движущуюся части сцены соответственно. ( F ) События, связанные с движущимися препятствиями. Этот кадр используется для разделения различных динамических объектов в сцене.
Положение и скорость каждого препятствия относительно камеры затем передавались в алгоритм быстрого уклонения, разработанный для использования малой задержки срабатывания.Для этого мы использовали схему реактивного избегания, основанную на использовании искусственных потенциальных полей ( 40 ), основанную на быстрых геометрических примитивах для представления препятствий, что делает ее недорогой в вычислительном отношении. Мы предложили формулировку поля отталкивания, которая лучше подходит для задачи обхода быстро движущихся препятствий, учитывая необходимость быстрой реакции робота при обнаружении препятствия. По сравнению с предыдущими подходами, наша формулировка потенциала отталкивания увеличивалась значительно быстрее, поскольку расстояние между роботом и препятствием уменьшалось, чтобы сделать маневр уклонения более реактивным и гибким.Кроме того, мы рассмотрели как величину, так и направление скорости препятствия, чтобы решить, в каком направлении уклоняться, и ввели коэффициент уменьшения величины потенциала, чтобы учесть, что препятствия, которые мы рассматриваем, являются динамическими; т.е. они не занимают одно и то же положение во времени.
Наш подход ставит во главу угла скорость вычислений, а не точность; поэтому мы жертвуем точностью обнаружения ради задержки. Тем не менее, мы показываем, что наш алгоритм в среднем использует только 3.5 мс (с момента получения событий для обработки до момента отправки первой команды, чтобы избежать обнаруженных препятствий) для обнаружения движущихся препятствий с ошибкой положения, обычно порядка нескольких десятков сантиметров. Торговля точностью обнаружения для задержки является необходимостью не только для роботизированных платформ, но также часто наблюдается у животных ( 41 ) для выполнения нескольких задач, связанных с визуальным восприятием.
Мы продемонстрировали эффективность нашего подхода в реальных экспериментах с квадрокоптерной платформой.Мы проверили нашу систему как с монокуляром (для препятствий известного размера), так и со стереосистемой (для препятствий неизвестного размера) как в помещении, так и на открытом воздухе. Вся структура предотвращения столкновений может работать в реальном времени на небольшом одноплатном компьютере на борту транспортного средства вместе со всем программным стеком, необходимым для полета робота (т.е. оценка состояния, высокоуровневое управление и связь с полетом контроллер). Экспериментальные результаты показывают, что наша конструкция позволяла квадрокоптеру избегать препятствий, движущихся к нему с относительной скоростью до 10 м / с с расстояния около 3 м.Интеграция известных методов обнаружения препятствий на основе событий ( 23 ) и предотвращения ( 40 ), адаптированная для того, чтобы позволить всей структуре работать в реальном времени на небольшом компьютере, а также справляться с быстрыми действиями. движущиеся препятствия, представляет собой основной вклад данной статьи.
РЕЗУЛЬТАТЫ
Точность и коэффициент успешности
Мы собрали набор данных из более чем 250 бросков, получили около 1200 обнаружений и сравнили выходные данные нашего детектора на основе событий с наземными данными системы захвата движения.Для каждого обнаружения мы вычислили норму ошибки местоположения и в таблице 1 суммировали результаты.
Таблица 1 Точность нашего основанного на событиях алгоритма обнаружения движущихся препятствий.Мы проанализировали как монокуляр, так и стереосистему и сравнили обнаружение с достоверными данными, предоставленными системой захвата движения. Для каждой конфигурации мы сообщаем (выраженные в метрах) среднее значение, медианное значение, стандартное отклонение и максимальное абсолютное отклонение (M.A.D.) нормы ошибки местоположения для различных диапазонов расстояний.
Мы сгруппировали измерения, попадающие в интервалы 0,5 м, причем первое из них начиналось с расстояния 0,2 м вдоль оптической оси камеры, поскольку алгоритм не смог успешно обнаружить препятствия на более близких расстояниях. В случае с монокулярным детектором необходимо было отбросить некоторые данные, которые мы собрали из-за того, что на небольших расстояниях препятствие часто было только частично видимым, и, следовательно, наш алгоритм монокуляра не смог правильно оценить его расстояние, потому что он соответствовал бы известному размеру частично видимому объекту.Эта проблема стала менее заметной по мере увеличения расстояния до камеры, и через 1 м она не оказала существенного влияния на работу детектора. С другой стороны, как и ожидалось, стереоконфигурация была более точной на низких дистанциях: чем дальше расстояние между камерами и объектом, тем выше неопределенность триангуляции и, следовательно, больше ошибка.
Однако, независимо от конфигурации, данные в таблице 1 показывают, что наш алгоритм, хотя и не адаптирован к точности, а скорее оптимизирован для малой задержки, обеспечивает измерения, которые достаточно точны, чтобы позволить квадрокоптеру воспринимать окружающее пространство и эффективно обнаруживать движущиеся препятствия. .Погрешность определения местоположения в среднем меньше, чем размер транспортного средства, тогда как SD немного выше, но все же разумно до 1 м. Среди факторов, влияющих на ошибку в оценке положения препятствий, низкое разрешение камеры, безусловно, играет ключевую роль.
Еще один важный аспект, который следует учитывать в нашем алгоритме обнаружения, — это его успешность. Чтобы вся структура была эффективной, она должна не только гарантировать низкую задержку, но и гарантировать надежность с точки зрения вероятности успеха.Чтобы оценить надежность нашего алгоритма, мы провели оценку с объектами разных размеров и форм. Такие объекты пропускались через поле зрения датчиков, и, используя внутреннюю калибровку камеры и наземные данные системы захвата движения, мы получили информацию о том, когда они должны были быть видимыми. Если объект находился в поле зрения камер, но система не сообщала об обнаружении, мы расценивали это как сбой алгоритма обнаружения.Это позволило нам проанализировать степень успешности нашего алгоритма обнаружения движущихся объектов, которая представлена в таблице 2. Мы использовали объекты размером до 30 см, а в таблице мы сгруппировали объекты, принадлежащие к трем различным категориям: меньше, чем 10 см, менее 20 см и до 30 см. Для каждой категории мы предоставили данные об успешности, когда объекты перемещаются на разное расстояние от камеры, и сгруппировали обнаружения в соответствии с этим расстоянием. Как можно заметить, наш алгоритм обеспечивал высокие показатели успешности в различных сценариях, как с маленькими, так и с большими объектами.Учитывая ограниченные поля зрения камер, большие объекты имеют более низкую скорость обнаружения на коротких расстояниях, в основном из-за их различного внешнего вида в двух камерах, используемых в стереосистеме, что затрудняет согласование алгоритма с отдельными обнаружениями. Точно так же небольшие объекты труднее обнаружить на больших расстояниях из-за ограниченного углового разрешения сенсора, используемого для экспериментов. Кроме того, мы не заметили какого-либо существенного влияния скорости объектов или угла падения на вероятность успеха.
Таблица 2 Показатель успешности детектора событий.Каждый столбец сообщает об успешности перемещения объектов на определенном расстоянии от камеры. Каждая строка показывает степень успешности обнаружения объектов меньше определенного размера. Результаты получены на наборе данных, состоящем из 100 бросков объектов каждого размера.
Вычислительные затраты
Бросая объекты в поле зрения камеры событий, одновременно вращая ее и измеряя время, необходимое для обработки всех событий, сработавших в течение последнего временного окна в 10 мс, мы могли бы количественно оценить вычислительные затраты нашего алгоритма обнаружения.В таблице 3 показаны результаты нашей оценки, подчеркивая, как каждый шаг алгоритма влияет на общее время вычислений. Наша оценка проводилась на плате NVIDIA Jetson TX2 с алгоритмом, работающим исключительно на центральном процессоре (то есть графический процессор, доступный на той же плате, не использовался вообще). Цифры, приведенные в таблице 3, относятся ко времени, необходимому для запуска алгоритма обнаружения с одной камерой; однако выполнение нескольких экземпляров одного и того же алгоритма для нескольких камер (как, например, в случае стерео) не повлияло существенно на производительность, поскольку отдельные части могут вычисляться параллельно.
Таблица 3 Среднее значение μ и стандартное отклонение σ времени вычисления алгоритма обнаружения препятствий.Самая дорогая часть алгоритма — это компенсация движения эго, которая в среднем требует 1,31 мс (36,80% от общего времени) с SD 0,35 мс. Время, необходимое для этого шага, зависит от количества событий, которые необходимо обработать, и рис. S4 показывает линейную зависимость между ними. Чтобы понять, сколько событий обычно генерируется в реальных сценариях во время наших экспериментов, мы собрали некоторую статистику о количестве событий, которые алгоритм должен обработать.Собранные данные показали, что в среднем как в помещении, так и на улице количество событий, относящихся к временному окну 10 мс, охватывает период от 2000 до 6000.
Еще одним шагом, который зависит от относительного движения между камерой и сценой, является кластеризация событий, относящихся к динамическим препятствиям. Этот шаг необходим, чтобы понять, сколько объектов находится в сцене, и связать с ними каждое событие. Для кластеризации событий обычно требуется 0,69 мс (19,39% от общего времени) со стандартным отклонением 0.20 мс. Фактическое время обработки для кластеризации событий зависит от количества пикселей, в которых возникли события, принадлежащие динамическим препятствиям, и рис. S5 показывает, сколько времени занимает наш алгоритм кластеризации в зависимости от количества пикселей для обработки.
Наконец, определение порога изображения средней отметки времени и применение некоторых морфологических операций к изображению с пороговым значением не зависят от количества событий, которые должны быть обработаны (как показано их очень низкими SD), потому что все изображение должно быть обработано, и они требовали в среднем 0.98 мс (27,52%) и 0,58 мс (16,29% от общего времени) соответственно.
Важно отметить, что при оценке вычислительного времени алгоритма мы пренебрегли оценкой трехмерного положения препятствия. Этот шаг требует очень простых вычислений, которые не зависят от количества сгенерированных событий и, в среднем, требуют времени порядка нескольких микросекунд. Следовательно, их влияние на общее время вычислений незначительно.
Различные типы препятствий
Основная причина, по которой мы выбираем стереоконфигурацию для нашей структуры, — это необходимость правильно обнаруживать движущиеся препятствия независимо от их формы и размера.Это невозможно при использовании одной камеры, если размер препятствия не известен заранее. На рисунке S5 показано, что алгоритм, который мы предлагаем в этой статье для обнаружения движущихся препятствий с помощью двух камер событий, способен обнаруживать различные типы препятствий. На этом рисунке можно обнаружить препятствия совершенно разной геометрии: маленький шар, коробку, маркер для белой доски, летающую тарелку, квадрокоптер и кеглю для боулинга. Первый столбец сообщает о кадре, захваченном камерой SEES1, где объект часто не был виден из-за размытия движения (мы вручную выделили область, где объекты находятся в кадре, красным кружком).Остальные столбцы отображают ранее описанные шаги нашего алгоритма обнаружения с тем же цветовым кодом, что и на рис. 4.
Обнаружение нескольких одновременных препятствий
Наш конвейер может одновременно справляться с несколькими препятствиями, движущимися по сцене, благодаря процесс кластеризации и этап ассоциации измерений, описанный в разделе «Материалы и методы». На рисунке S6 показан пример, в котором предложенный алгоритм правильно обнаруживает и группирует события, относящиеся к трем различным движущимся препятствиям в сцене.В этом случае три небольших шара (вручную выделенных красным кружком для облегчения понимания читателем) были брошены перед камерой, и алгоритм успешно связал каждое событие с соответствующим объектом.
Основное ограничение нашего подхода связано с тем, что, когда два или более препятствия находятся очень близко друг к другу в кадре, содержащем события, принадлежащие динамическим объектам, очень трудно, если не невозможно, устранить неоднозначность между ними. . Это связано с тем, что не используется предварительная информация о препятствиях (например,g., форма или, в случае стерео, размер), а также отсутствие использования какой-либо информации об интенсивности (т. е. кадров с бортовой камеры) для различения объектов, которые невозможно сегментировать, используя только события. В нашей экспериментальной оценке это оказалось не реальной проблемой для самой системы, потому что как только перекрывающиеся препятствия удалялись друг от друга, система могла быстро обнаруживать их и рассматривать как отдельные объекты.
Валидация схемы обхода препятствий
Для проверки нашей схемы избегания препятствий мы провели большой набор экспериментов в реальных сценариях.Эксперименты проводились в двух разных сценариях: в помещении и на открытом воздухе. Эксперименты в помещении проводились в системе захвата движения, в той же установке, которую мы использовали в нашей предыдущей работе ( 8 ), и преследовали двоякую цель: (i) сбор достоверных данных для проверки эффективности системы в ситуациях, когда столкновение с препятствием могло бы произойти (что было проверено в постобработке благодаря данным захвата движения) и (ii) проверка общей структуры в более простой настройке перед переходом к более сложным сценариям.Мы использовали ту же платформу квадрокоптера, которую мы представили в ( 8 ) для экспериментов в помещении, оснащенную монокулярной установкой. Напротив, эксперименты на открытом воздухе проводились с использованием другого транспортного средства, оснащенного стереосистемой.
Эксперименты в помещенииОсновная цель экспериментов в помещении состояла в том, чтобы определить эффективность нашей системы, позволяющей избежать динамических препятствий, путем определения того, действительно ли столкновение было предотвращено, путем анализа данных, поступающих от системы захвата движения.Эксперименты в помещении проводились с использованием той же платформы, описанной в ( 8 ), в монокулярной установке. Мы неоднократно бросали шар известного размера в квадрокоптер, который использовал камеру событий, чтобы обнаружить и избежать его. Используя наземные измерения, поступающие от системы захвата движения OptiTrack, мы могли пересечь траекторию мяча с положением, в котором зависло транспортное средство, чтобы определить, попадет ли мяч в транспортное средство без выполнения маневра эвакуации. .Результатом этого анализа является то, что наш алгоритм был способен предотвращать фактические столкновения между летающим роботом и динамическими препятствиями на относительной скорости до 10 м / с, что подтверждается достоверными данными о траектории объекта, обеспечиваемыми движением. система захвата.
На рис. 5 показан один из экспериментов в помещении, в котором представлены четыре снимка, сделанные статической камерой. Мячу потребовалось около 0,25 с, чтобы достичь транспортного средства с момента его броска (рис. 5А). В то время, как показано на рис.5D, квадрокоптер уже переместился в сторону, чтобы предотвратить столкновение, показывая, что алгоритм успешно обнаружил мяч и спланировал маневр уклонения с очень малой задержкой.
Рис. 5 Последовательность одного из экспериментов в помещении.Мяч брошен в сторону транспортного средства, оборудованного монокулярной камерой событий, которая используется для обнаружения препятствия и уклонения от него. ( A ) t = 0 с. ( B ) t = 0,075 с. ( С ) т = 0.15 с. ( D ) t = 0,225 с. Мяч бросается в момент времени t = 0 с и достигает положения, в котором квадрокоптер зависает примерно в момент времени t = 0,225 с. Робот успешно обнаруживает приближающееся препятствие и перемещается в сторону, чтобы его избежать.
Эксперименты на открытом воздухеПосле оценки производительности нашего каркаса в помещении, мы выполнили эксперименты на открытом воздухе, используя платформу квадрокоптера, оборудованную двумя камерами Insightness SEES1 в стереосистеме.Мы выполнили два типа экспериментов: в статическом сценарии, когда транспортное средство зависает в желаемом положении, и в динамическом сценарии, когда робот летит к целевому местоположению. В обоих случаях мы бросали различные объекты в квадрокоптер, который полагался только на две камеры событий, чтобы обнаруживать их и избегать их.
Мы протестировали производительность нашего алгоритма в статических сценариях с разными типами объектов, с множеством препятствий, движущихся к нему в одно и то же время, а также с их последовательным перебрасыванием одного за другим, чтобы оценить беспокойство всего подхода.Транспортному средству удавалось их обнаруживать и избегать в большинстве случаев, хотя в некоторых случаях обнаружение не было успешным и приводило к столкновению робота с препятствиями. Позже мы обсудим основные причины сбоев нашего алгоритма; тем не менее, в экспериментах на открытом воздухе алгоритм успешно обнаруживал и избегал препятствий, с которыми он сталкивался, более чем в 90% случаев.
На рисунке 6 показаны четыре моментальных снимка, снятых из последовательности, записанной в динамическом сценарии.Робот двигался к целевой позиции слева направо на изображениях с линейной скоростью 1,5 м / с. Достигнув места назначения, робот обнаружил брошенный в него желтый шар (показан справа на рис. 6A). Транспортное средство решило выполнить маневр уклонения вверх, сохраняя при этом постоянную скорость движения в направлении желаемого положения. Это привело к маневру, который одновременно позволил транспортному средству продолжить выполнение своей задачи и избежать столкновения. Дополнительные эксперименты в динамической ситуации показаны в фильме S1.
Рис. 6 Последовательность наших экспериментов на открытом воздухе.( A ) t = 0 с. ( B ) t = 0,15 с. ( C ) t = 0,30 с. ( D ) t = 0,45 с. Квадрокоптер летит к исходной целевой позиции, когда к нему бросается препятствие. Препятствие успешно обнаруживается с помощью стереопары камер событий и избегается движением вверх.
Ограничения датчиков событий
Как мы уже показали, камеры событий позволяют быстро обнаруживать движущиеся препятствия с малой задержкой.Мы обсудили преимущества этих нейроморфных датчиков с биоинспирированием по сравнению со стандартными камерами. Однако на сегодняшний день они в основном являются сенсорами, ориентированными на исследования, и поэтому все еще требуют значительных инженерных усилий для решения основных проблем, которые они представляют.
Одна из проблем современных камер для событий — их вес. Большинство доступных в настоящее время камер для мероприятий больше и тяжелее, чем современные стандартные камеры для роботизированных приложений, которые обычно имеют вес менее 50 г. Insightness SEES1, насколько нам известно, является самой маленькой камерой для событий, которая также обеспечивает кадры (что особенно удобно для простой калибровки внутренних и внешних параметров датчика) и может быть легко установлена на квадрокоптер (ее размер 3 .5 см на 3,5 см, а вес — 15 г). Однако его разрешение [320 пикселей на 240 пикселей, QVGA (Quarter Video Graphics Array)] особенно низкое по сравнению со стандартными камерами. Это налагает необходимость найти правильный компромисс между полем зрения и угловым разрешением: чем больше первое, тем меньше второе, что уменьшает диапазон зондирования, на котором можно надежно обнаруживать объекты ( 8 ) . Однако небольшое поле зрения отрицательно сказывается на обнаружении препятствий, попадающих в зону действия транспортного средства сбоку, как, например, в наших динамических экспериментах на открытом воздухе: чем больше поле зрения, тем раньше транспортное средство может обнаруживать и избегать препятствий, движущихся к нему с боков.
Другой проблемой, характеризующей эти датчики, являются их шумовые характеристики. Эти датчики показывают более высокий уровень шума, чем стандартные камеры, что часто отрицательно сказывается на производительности алгоритмов видения, основанного на событиях. В нашем подходе, например, для получения надежных обнаружений и исключения ложных срабатываний, вызванных шумом датчика, нам пришлось существенно увеличить порог, используемый для отделения событий, генерируемых статической частью сцены, от событий, вызванных движущимися объектами.Это привело к тому, что алгоритм обнаружения препятствий стал менее реагировать на небольшое относительное движение, особенно на больших расстояниях. По этой причине мы отбросили все обнаружения, сообщающие о расстоянии между камерой и препятствием более 1,5 м.
Вышеупомянутые причины представляют собой основные причины неудач нашего подхода. В большинстве случаев, когда наш квадрокоптер не мог избежать брошенного в него объекта, это было связано с тем, что он был обнаружен слишком поздно, либо потому, что он попал в поле зрения камеры на слишком большом расстоянии. короткое (и, следовательно, транспортное средство не могло завершить маневр уклонения вовремя) или потому, что движение препятствия не вызвало достаточного количества событий, чтобы наш алгоритм мог его обнаружить.
Благодарности: Мы благодарим Х. Ребека и Г. Галлего за полезные обсуждения. Финансирование: Эта работа была поддержана стартовым грантом SNSF-ERC и Швейцарским национальным научным фондом через Национальный центр компетенции в исследованиях (NCCR) робототехники. Вклад авторов: Идеи проекта были разработаны Д.Ф., К.К. и Д.С.Эксперименты были разработаны и выполнены Д.Ф. и К.К. Статья написана D.F., K.K. и D.S. Конкурирующие интересы: Авторы заявляют, что у них нет конкурирующих интересов. Доступность данных и материалов: Все данные, необходимые для оценки выводов в статье, представлены в статье или дополнительных материалах.
Избегание препятствий — обзор
9.7 Навигация в среде, загроможденной движущимися препятствиями
В этом разделе мы следуем принципам главы 6 и применяем алгоритм пограничного патрулирования к более общей проблеме безопасного управления автономным колесным транспортным средством. робот к цели в заранее неизвестной загроможденной среде.Как и в главе 6, этот алгоритм используется для обхода препятствий на пути с заранее определенным запасом прочности, в то время как робот направляется прямо к цели, когда это возможно. Правила, регулирующие переключение между режимами уклонения от препятствий и движения по прямой к цели, соответственно, в основном заимствованы из главы 6. Новизна по сравнению с главой 6 состоит в том, что препятствия не являются устойчивыми, но могут совершать произвольные движения, в том числе повороты и деформации. .
В частности, мы предполагаем, что помимо робота существует неподвижная точечная цель T и несколько постоянно непересекающихся движущихся препятствий D 1 ( t ),…, D k ( t ) в самолете.Цель состоит в том, чтобы подвести робота к цели через свободную от препятствий часть плоскости: r (t) ∉⋃i = 1kDi (t) ∀t. Кроме того, должен соблюдаться заданный запас прочности:
distr (t); Di (t) ≥dsafe≥0∀t, i.
Предлагаемый нами навигационный контроллер переключается между законом уклонения от препятствий (3.1) и прямым движением к цели:
(7.1) u (t) = 0.
In (3.1), d 0 > d safe теперь настраиваемый параметр контроллера (желаемое расстояние до препятствия при его обходе) и d ( t ) заменяется by di (t): = distr (t); Di (t) для i , выбранного контроллером.Еще два параметра контроллера:
- •
ϵ > 0 — участвует в принятии решения о прекращении объезда препятствия, что допускается только при достаточно близком приближении робота к препятствию: d i ≤ д 0 + ϵ ;
- •
C > d 0 + ϵ — порог срабатывания: расстояние до препятствия, на котором включается режим уклонения.
Переключение (7.1) ↦ (3.1) происходит, когда расстояние d i до препятствия D i ( t ) уменьшается до C , при этом i используется d : = d i в (3.1). Обратное (3.1) ↦ (7.1) выполняется, когда d i ( t ) ≤ d 0 + ϵ и робот направляется к цели.Чтобы это правило было четко определено, (3.1) не должно активироваться одновременно для нескольких препятствий. Чтобы предложить конструктивные условия для этого, введем следующее.
Определение 7.1
Усредненный пролет препятствия i равен Riav = minRi, где min по всему Ri, так что в течение любого временного интервала продолжительности (3π) / u¯ тело D i ( t ) остается в некотором устойчивом диске радиуса Ri.
По iii теоремы 5.1, с момента начала маневра уклонения на расстоянии C от препятствия i и до начала скользящего движения в направлении d 0 -эквидистантной кривой робот движется внутри диска радиуса 2Rmin. с центром в исходном положении, где Rmin — минимальный радиус поворота (2.2). Тем временем препятствие перемещается в пределах некоторого диска радиуса Риав. Таким образом, на этом этапе расстояние d i от робота до препятствия постоянно лежит в интервале(7.2) di∈C − 2 (Rmin + Riav); C + 2 (Rmin + Riav).
Затем d i монотонно переходит в d 0 < C по теореме 5.1. Таким образом, пока правило навигации (3.1) активно для препятствия i , робот находится на расстоянии ≤C + 2 (Rmin + Riav) от D i ( t ). Таким образом, чтобы исключить одновременную активацию этого правила для двух препятствий, достаточно, чтобы они были разделены расстоянием> 2 (C + Rmin + Rmaxav), где Rmaxav: = maxiRiav.Что касается доступной свободы выбора C , d 0 , ϵ ( C > d 0 + ϵ , ϵ > 0, d 0 > d safe ), это приводит к следующему требованию к расстоянию d i , j ( t ) между любыми двумя препятствиями i ≠ j at в любое время т :
(7.3) di, j (t) ≥dobs> 2 (Rmin + Rmaxav + dsafe).
Тогда C , d 0 и ϵ можно и нужно выбрать так, чтобы
dobs2− (Rmin + Rmaxav)> C> d0 + ϵ, ϵ> 0, d0> dsafe.
Поскольку закон навигации (3.1) все еще применяется, должны выполняться условия его сходимости. Мы предполагаем, что предположения 4.1 и 4.2 верны для любого препятствия. Если C≥2 (Rmin + Rmaxav), вышеупомянутые два диска не пересекаются (см. Рис. 9.13) и поэтому могут быть разделены прямой линией; Таким образом, Предположение 4.7 удержаний. Такой выбор C возможен, только если dobs> 6Rmin + 6Rmaxav в дополнение к (7.3), которое предполагается. Соответственно, C следует выбрать так, чтобы
Рисунок 9.13. Непересекающиеся диски.
(7,4) dobs2− (Rmin + Rmaxav)> C> maxd0 + ϵ; 2 (Rmin + Rmaxav).
Что касается предположения 4.6, отметим, что в силу (7.2) все дистанции запуска для любого маневра обхода препятствия и содержатся в интервале из (7.2) и, следовательно, в
(7.5) C − 2 (Rmin + Rmaxav); C + 2 (Rmin + Rmaxav).
Итак, предположение 4.6 может быть выполнено, если в пределах диапазона (7.4) существует значение C такое, что C − 2 (Rmin + Rmaxav)> dsafe, и интервал (7.5) является регулярным для любого препятствия, при условии, что что d 0 выбрано в пределах этого интервала. В целом, мы приходим к следующим рекомендациям по выбору C , d 0 , ϵ :
(7,6) 2 (Rmin + Rmaxav)> ϵ> 0, dobs2− (Rmin + Rmaxav) > d0> dsafe, mindobs2− (Rmin + Rmaxav); d0 + 2 (Rmin + Rmaxav)> C> maxd0 + ϵ; 2 (Rmin + Rmaxav) + dsafe.
Это возможно тогда и только тогда, когда dobs> 6Rmin + 6Rmaxav + 2dsafe.
Для правильного выбора параметров контроллера γ и δ достаточно выбрать вспомогательные параметры z * , λ a , λ v , η a , η v в (7.3) общее для всех препятствий. Это возможно: для каждого препятствия λ a , λ v дюймов (4.6) сначала увеличиваются (в пределах (0,1)) до общего значения, затем общие η v ∈ (0,1 — λ v ), η a Выбраны ∈ (0,1 — λ a ). Наконец, z * вычисляется для всех препятствий, и минимальный результат помещается в (7.3).
Для реализации предложенного закона наведения робот должен иметь доступ к углу визирования β ( t ) на цель T, а также к расстоянию d i и его производная d˙i, если di≤C + 2Rmin + 2Riav.Мы также предполагаем, что изначально робот находится выше порога срабатывания всех препятствий d i (0)> C ∀ i и что они всегда достаточно далеко от цели distT; Di (t) > d0 + ϵ∀t, т. Поскольку контроллер (3.1) все еще используется, условия (4.6) и (5.4) также должны быть воспроизведены.
В оставшейся части этой главы сходимость и эффективность предложенного закона наведения для достижения цели с уклонением от препятствий демонстрируются посредством обширного моделирования и экспериментальных исследований.Они представлены в следующих двух разделах.
Обход препятствий мобильными роботами с использованием модифицированного алгоритма искусственного потенциального поля | Журнал EURASIP по беспроводной связи и сети
В этом разделе сначала выполняется сравнение результатов моделирования алгоритма искусственного потенциального поля и модифицированного искусственного потенциального поля, затем отображается обход препятствий мобильным роботом на фоне множества препятствий. которые моделируются с использованием модифицированного алгоритма искусственного потенциального поля.
В алгоритме искусственного потенциального поля, в котором его отношение было сказано в разделе 2, если значение параметра рассматривается как Z = 100, M = 2, k S = 1,1, G 0 = 0,11 и L = 0,1 и препятствия на окружности радиуса R = 0,18, результат показан на рис. 8; робот застрял в ловушке и стоит на локальном минимуме. На рисунке 9 показано, что сила отталкивания больше силы притяжения на всех этапах, что означает, что робот находится в локальном минимуме.Если эти параметры изменяются в любой желаемой степени, кроме этих значений, статус робота на локальном минимуме не изменится. Сетчатый график этого моделирования показан на рис. 10. Он описывает препятствия, такие как вершина, полость действия цели и поглощение робота внутри себя.
Рис. 8Результат моделирования алгоритма искусственного потенциального поля для круговых препятствий радиусом R = 0,18
Рис. 9Количество энергии отталкивания и притяжения и их отдача в зависимости от количества шагов в алгоритм искусственного потенциального поля для круговых препятствий радиусом R = 0.18
Рис. 10Сетчатый график потенциальной энергии притяжения и отталкивания в алгоритме искусственного потенциального поля для круговых препятствий радиусом R = 0,18
В модифицированном алгоритме искусственного потенциального поля, в котором его связь была указана в Раздел 3, если значение параметра рассматривается как Z = 100, M = 2, k S = 1,1, G 0 = 0,11 и L = 0.1 и препятствия на окружности радиуса R = 0,18, результат показан на фиг. 11. Сравнивая фиг. 8 и 11 видно, что в алгоритме искусственного потенциального поля робот не может достичь цели и попадает в локальный минимум, но при тех же условиях в модифицированном алгоритме искусственного потенциального поля он достигает цели, избегая препятствия.
Рис. 11Результат моделирования модифицированного алгоритма искусственного потенциального поля для круговых препятствий радиусом R = 0.18
На рисунке 12 показано, что при количестве шагов около 200 витков сила притяжения обнуляется; это означает, что с таким количеством шагов робот достигает цели. Сетчатый график этого моделирования на рис. 13 показывает, что препятствия, такие как вершина и цель, действуют как полость и поглощают робота в себе.
Рис. 12Количество энергии отталкивания и притяжения и их отдача в соответствии с количеством шагов в модифицированном алгоритме искусственного потенциального поля для круговых препятствий радиусом R = 0.18
Рис. 13Сетчатый график потенциальной энергии притяжения и отталкивания в модифицированном алгоритме искусственного потенциального поля для круговых препятствий радиусом R = 0,18
В модифицированном алгоритме искусственного потенциального поля, в котором была указана его связь в разделе 3, если значение параметра рассматривается как Z = 100 , M = 2, k S = 1,1, G 0 = 5 и L = 0.1 и препятствия на окружности радиуса R = 40, результат показан на рис. 14. Он показывает, что робот достигает цели, избегая препятствий.
Рис. 14Результат моделирования модифицированного алгоритма искусственного потенциального поля для круговых препятствий радиусом R = 40
На рисунке 15 показано, что при количестве шагов почти 400 витков сила притяжения обнуляется; это означает, что с таким количеством шагов робот достигает цели.Сетчатый график этого моделирования на рис. 16 показывает, что препятствия, такие как вершина и цель, действуют как полость и поглощают робота в себе.
Рис. 15Количество энергии отталкивания и притяжения и их отдача в соответствии с количеством шагов в модифицированном алгоритме искусственного потенциального поля для кругового препятствия радиусом R = 30
Рис.16Сетчатый график потенциальная энергия притяжения и отталкивания в модифицированном алгоритме искусственного потенциального поля для круговых препятствий радиусом R = 30
В модифицированном алгоритме искусственного потенциального поля, в котором его связь была указана в разделе 3, если значение параметра равно рассматривается как Z = 100, M = 2, k S = 1.1, G 0 = 2,1 и L = 0,5 и препятствия на окружности с радиусом R = 7, результат показан на рис. 17. Это показывает, что робот достигает цели за счет избегание препятствий.
Рис. 17Результат моделирования круговых препятствий радиусом R = 7 в модифицированном алгоритме искусственного потенциального поля
На рисунке 18 показано, что при количестве шагов почти 700 витков сила притяжения обнуляется; это означает, что с таким количеством шагов робот достигает цели.Сетчатый график этого моделирования на рис. 19 показывает, что препятствия, такие как вершина и цель, действуют как полость и поглощают робота в себе.
Рис.18Количество энергии отталкивания и притяжения и их отдача в соответствии с количеством шагов в модифицированном алгоритме искусственного потенциального поля для круговых препятствий радиусом R = 7
Рис.19Сетчатый график потенциальная энергия притяжения и отталкивания в модифицированном алгоритме искусственного потенциального поля для круговых препятствий радиусом R = 7
В модифицированном алгоритме искусственного потенциального поля, в котором его связь была указана в разделе 3, если значение параметра равно .2 + 0,5; X \ in \ left (0,7,3,5 \ right) \), результат показан на рис. 20. Он показывает, что робот достигает цели, избегая препятствий.
Рис. 20Результат моделирования криволинейного препятствия в модифицированном алгоритме искусственного потенциального поля
На рисунке 21 показано, что при количестве шагов почти 1000 витков сила притяжения обнуляется; это означает, что с таким количеством шагов робот достигает цели. Сетчатый график этого моделирования на рис. 22 показывает, что препятствия, такие как вершина и цель, действуют как полость и поглощают робота в себе.
Рис. 21Количество энергии отталкивания и притяжения и их отдача в соответствии с количеством шагов в модифицированном алгоритме искусственного потенциального поля для криволинейного препятствия
Рис. 22Сетчатый график потенциальной энергии притяжение и отталкивание в модифицированном алгоритме искусственного потенциального поля для криволинейного препятствия
В модифицированном алгоритме искусственного потенциального поля, в котором его связь была указана в разделе 3, если значение параметра рассматривается как Z = 100, M = 2, k S = 1.1, G 0 = 0,3 и L = 0,1, и препятствие рассматривается как X = 4; 4 ≤ Y ≤ 7, результат показан на рис. 23. Это показывает, что робот достигает цели, избегая препятствий.
Рис. 23Результат моделирования прямого препятствия в модифицированном алгоритме искусственного потенциального поля
На рисунке 24 показано, что при количестве шагов почти 900 витков сила притяжения обнуляется; это означает, что с таким количеством шагов робот достигает цели.Сетчатый график этого моделирования на рис. 25 показывает, что препятствия, такие как вершина и цель, действуют как полость и поглощают робота в себе.
Рис.24Количество энергии отталкивания и притяжения и их отдача в соответствии с количеством шагов в модифицированном алгоритме искусственного потенциального поля для прямого препятствия
Рис.25Сетчатый график потенциальной энергии притяжения и отталкивание в модифицированном алгоритме искусственного потенциального поля для прямого препятствия
В модифицированном алгоритме искусственного потенциального поля, в котором его отношение было сказано в разделе 3, если значение параметра рассматривается как Z = 100, M = 2, к S = 1.1, G 0 = 0,2 и L = 0,03, и препятствие рассматривается как Y = 4; 4 ≤ X ≤ 6 и x = 4; 3 ≤ y ≤ 4, результат показан на рис. 26. Он показывает, что робот достигает цели, избегая препятствий.
Рис. 26Результат моделирования препятствия в виде ломаной линии в модифицированном алгоритме искусственного потенциального поля
На рисунке 27 показано, что при количестве шагов почти 700 витков сила притяжения обнуляется; это означает, что с таким количеством шагов робот достигает цели.Сетчатый график этого моделирования на рис. 28 показывает, что препятствия, такие как вершина и цель, действуют как полость и поглощают робота в себя.
Рис.27Количество энергии отталкивания и притяжения и их отдача в соответствии с количеством шагов в модифицированном алгоритме искусственного потенциального поля для препятствия из ломаной линии
Рис.28Сетчатый график потенциальной энергии притяжения и отталкивание в модифицированном алгоритме искусственного потенциального поля для препятствия из ломаной линии
Метод обхода препятствий в реальном времени для автономных транспортных средств с использованием гауссова потенциального поля, зависящего от препятствий
Новый метод обхода препятствий для автономных транспортных средств, называемый зависимый от препятствий гауссовский потенциальное поле (ODG-PF) спроектировано и реализовано.Он обнаруживает препятствия и рассчитывает вероятность столкновения с ними. В этой статье мы представляем новый метод расчета поля притяжения и отталкивания, а также подход к решению о направлении. Моделирование и эксперименты были выполнены и сравнены с другими методами предотвращения препятствий на основе потенциального поля. Результаты показывают, что ODG-PF показал наилучшие результаты в большинстве случаев.
1. Введение
Автономным системам транспортных средств требуется планирование пути, локализация внутри и снаружи помещений, обход препятствий, обнаружение объектов и классификация автомобилей, людей, домашних животных, дорожных знаков, сигналов и т. Д.
Планирование пути — одна из фундаментальных технологий в автомобильной технике. В планировании пути есть две категории, а именно: глобальное планирование пути и локальное планирование пути. Для глобального планирования пути требуется информация из географической информационной системы (ГИС) и глобальная локализация, в то время как для локального планирования маршрута требуется относительное положение и избегание препятствий. Существует множество алгоритмов как глобального, так и локального планирования пути. При глобальном планировании пути для построения графа используются графические методы, такие как алгоритм Вороного [1–4], алгоритм декомпозиции ячеек [5–7] и алгоритм быстрого перехода [4, 8, 9], а затем поиск кратчайшего путь к цели.
Предотвращение препятствий — одна из важнейших технологий при планировании локальных маршрутов и одна из важнейших технологий, гарантирующих безопасность людей и транспортных средств. На протяжении десятилетий по этой теме было проведено множество исследований и разработано множество методов, некоторые из которых были реализованы в реальных системах. Чтобы избежать столкновения с препятствиями, роботу необходимо не только обнаруживать препятствия, но и пересчитывать обходной путь и направлять себя в сторону безопасного и эффективного пути в режиме реального времени.
Хатиб [10] сформулировал концепцию метода искусственного потенциального поля (PFM) для реализации системы предотвращения препятствий. Этот метод, состоящий из поля притяжения и поля отталкивания, прост и легок в вычислительном отношении. Два разных поля вычисляются и суммируются, после чего робот следует направлению вычисленного вектора. Обход препятствий достигается за счет поля отталкивания, а направление к цели — за счет поля притяжения. Концепция искусственных потенциальных полей может также использоваться в качестве глобального планировщика пути [11].
Алгоритм ошибки был введен Люмельским и Степановым [12], в котором транспортное средство движется вдоль стены препятствия, когда оно встречается. Если направление к цели снова доступно, машина покидает препятствие и направляется к цели.
Боренштейн и Корен [13] представили другой метод, позволяющий избежать препятствий, названный методом гистограммы векторного поля (VFH), а Ульрих и Боренштейн [14] улучшили метод, приняв во внимание размер роботов и выбрав безопасный и эффективный угол (VFH +: позже модернизирован до VFH [15]).
Метод динамического окна (DWA) с использованием динамики транспортного средства был предложен в [16]. Этот метод состоит из трех окон скорости-угловой скорости: первое окно — это окно от минимальной до максимальной скорости-угловой скорости транспортного средства, второе — это зона без препятствий в первом окне, а последнее — доступная угловая скорость. окно скорости, возможное из текущей пары скорость-угловая скорость. На пересечении трех окон DWA выбирает пару скорость-угловая скорость, максимизируя целевую функцию.
Андерсон и др. [17] использовали управление с прогнозированием модели (MPC) для разработки метода планирования пути на основе оптимального управления, который использует относительно новый метод управления для прогнозирования движения транспортного средства. Главный недостаток этого подхода заключается в том, что это, по сути, нелинейная задача оптимального управления, и даже когда проблема может быть линеаризована, найти оптимальный путь в реальном времени непросто. Это сильно зависит от производительности процессора.
Метод диаграммы близости (ND) был предложен Мингесом и Монтано [18], которые классифицировали реальные ситуации на пять категорий, каждая из которых имеет свою процедуру принятия решений.Позднее этот метод был усовершенствован рядом других исследователей [19–21].
Метод следования зазором (FGM) был разработан Сезером и Гокасаном [22], в котором определяется угол максимального зазора, а затем вычисляется средневзвешенное значение угла и угла к цели.
Park et al. [23] разработали усовершенствованный метод нечеткого потенциального поля (AFPFM) как улучшенный алгоритм обычного PFM с использованием нечеткого членства и нечеткого вывода TS [24]. В этом методе поле притяжения AFPFM такое же, как и у обычного PF, но расчет поля отталкивания выполняется с использованием нечеткого вывода TS.
Для обнаружения препятствий используются многие виды датчиков, такие как гидролокатор, лазерный дальномер, лидар, стереовидение и трехмерный датчик глубины. В этом исследовании мы использовали лазерный дальномер и представили новый метод избежания препятствий, который мы называем методом гауссова потенциального поля, зависящего от препятствий (ODG-PF), который мы сравнили с PFM, FGM и AFPFM.
Эта статья состоит из 6 разделов. Раздел 1 — это введение. Алгоритмы сравнения с ODG-PF упомянуты в разделе 2.Раздел 3 подробно описывает ODG-PF. Результаты моделирования представлены в Разделе 4. Соответствующие эксперименты на открытом воздухе приведены в Разделе 5. Заключение находится в Разделе 6.
2. Сопутствующие работы
Во всех следующих методах используется датчик дальности. Синие линии на рисунке 1 (а) — это инфракрасные лазерные лучи, используемые для измерения расстояния. Как показано на Рисунке 1 (b), данные лазерного дальномера представляют собой расстояния, соответствующие заранее заданным углам в датчике.
Эти данные о расстоянии обрабатываются по-разному в разных алгоритмах.
2.1. Традиционный метод потенциального поля
По сути, методы, основанные на потенциальном поле, используют искусственное потенциальное поле, состоящее из поля притяжения и поля отталкивания. Притягивающее поле притягивает автомобиль к цели, а поле отталкивания отталкивает его от препятствий. Следующие уравнения отображают обычные расчеты потенциального поля: где.
Уравнение (1) показывает вычисление общего поля, в то время как поле притяжения, которое «притягивает» транспортное средство к цели, вычисляется по (2), где — вектор положения целевой точки, а — вектор положения транспортного средства.Уравнение (3) — это расчет поля отталкивания, которое отталкивает транспортное средство от препятствий, в котором находится вектор положения каждого препятствия. На рис. 2 показаны поле притяжения и поле отталкивания.
Как показано на рисунке 3, традиционный метод потенциального поля имеет недостаток в том, что он легко застревает в локальных минимумах [25].
2.2. Метод Follow-the-Gap
FGM не основан на искусственном потенциальном поле, но его решение угла гильдии в чем-то похоже.Кроме того, его методы обнаружения препятствий и пробелов в чем-то напоминают наш ODG-PF.
Основная идея FGM состоит в том, чтобы найти максимальный зазор перед автомобилем и сначала вычислить средний угол зазора (). Из полученных данных мы знаем, где находятся препятствия, и нам следует увеличить препятствия до некоторой степени с учетом ширины транспортного средства. Увеличивая препятствия, мы можем легко узнать, подходит ли проезд для транспортного средства или нет. Этот метод также определяет угол по направлению к цели, для которого решение о направлении принимается с использованием средневзвешенного значения угла максимального зазора и угла по направлению к цели.
В примере на рисунке 1 максимальный зазор находится в диапазоне от -14 ° до 18 °, а средний угол (2 °) становится таким, как показано на рисунке 4. Направляющий угол выбирается путем вычисления средневзвешенного значения и следующим образом : где — это минимальное расстояние от всех данных о расстоянии от датчиков дальности, и это значение, которое мы должны решить, чтобы избежать препятствия и эффективно двигаться к цели. Если он маленький, транспортное средство будет двигаться прямо к цели, но с большей вероятностью столкнется с препятствиями, тогда как если оно велико, транспортное средство будет двигаться более безопасно, но путь к цели не будет таким эффективным.Если автомобиль находится рядом с препятствием, он будет маленьким и станет больше, поэтому автомобиль будет двигаться скорее навстречу, чем навстречу. Если транспортное средство находится далеко от любых препятствий, оно станет большим и относительно небольшим, поэтому транспортное средство будет двигаться прямо навстречу.
2.3. Усовершенствованный метод нечеткого потенциального поля
Расчет силы отталкивания в AFPFM отличается от такового в обычном PFM. Следующее уравнение показывает расчет силы отталкивания в AFPFM: где — максимальный диапазон датчика расстояния, — это термин безопасности, учитывающий внешний корпус транспортного средства, — это коэффициент поля отталкивания, имеющий в основном то же значение, что и у PFM, и — это вес. что в нечеткой TS является минимальным значением трех функций принадлежности, и.Подробные процедуры расчета объяснены в [23].
3. Гауссово потенциальное поле, зависящее от препятствий
Здесь мы представляем ODG-PF. Основная идея этого метода заключается в том, что после получения данных о расстоянии от датчика (ов) дальности (как показано на рисунке 1 (b)) мы рассматриваем только те объекты, которые находятся в пределах порогового диапазона (например, 2 м), увеличить препятствия относительно ширины транспортного средства и построить из них гауссовское (отталкивающее) потенциальное поле. Затем мы вычисляем поле притяжения на основе информации об угле рыскания, полученной от инерциального измерительного блока (IMU).Суммарное поле состоит из этих двух полей, и из него мы выбираем угол с минимальным общим значением поля. На рисунке 5 представлена блок-схема всего процесса.
Если некоторые данные пространственно непрерывны в пределах порогового значения, они распознаются как препятствие. Эллипсы на рисунке 6 показывают, что есть два препятствия. Затем мы вычисляем среднее расстояние до каждого препятствия (и угол, занимаемый им. На рисунке 6 средние расстояния до препятствий 1 и 2 равны 1.99 и 1,36 м и соответствующие углы (занимаемые препятствиями составляют 1,5 и 51,5 ° соответственно.
В реальных системах мы должны учитывать ширину транспортного средства, и во многих алгоритмах ширина или размер транспортного средства добавляются к размер препятствия и размер транспортного средства уменьшаются до нуля. На рисунке 7 показан процесс увеличения препятствия.
Если мы учитываем ширину транспортного средства, нам необходимо пересчитать угол, поскольку где находится среднее расстояние до препятствия k th .
Как описано в (6), получается из среднего расстояния каждого препятствия и занятого угла препятствия. Яркие полосы, добавленные к левой и правой сторонам темной полосы на рисунке 7, представляют собой увеличение препятствия с учетом ширины транспортного средства. Если требуется больше безопасности, мы можем добавить больше запаса к ширине автомобиля.
Гауссовские функции правдоподобия (поля отталкивания) препятствий вычисляются как где — центральный угол каждого препятствия. Это функция.Нижний индекс i означает, что i -й сегмент данных данных датчика (i = 1… 361), и это порядковый номер каждого угла. Каждая гауссова функция правдоподобия становится компонентом отталкивающего поля. Коэффициент должен быть установлен таким образом, чтобы гауссова вероятность каждого препятствия полностью охватывала угол, занимаемый каждым препятствием. Впоследствии Таким образом, где. это максимальная дальность обнаружения датчика дальности и составляет половину угла, занимаемого препятствием k th .
На Рисунке 8 (а) показаны углы, занимаемые препятствиями, и гауссовы вероятности препятствий. Это объясняет, что вероятность каждого препятствия по Гауссу полностью охватывает занимаемый угол при.
Мы получаем поле отталкивания, суммируя все гауссовские функции правдоподобия препятствий в одну функцию, поскольку это также функция угла. Поле притяжения рассчитывается как Общее поле рассчитывается путем сложения этих двух полей. Поскольку эти два поля являются функциями, общее поле также является функцией: В (11) — это значение, которое мы должны выбрать (как в PFM и AFPFM).Если он слишком мал, транспортное средство будет избегать препятствий, но путь будет неэффективным, а если он слишком велик, у транспортного средства будет больше шансов столкнуться с препятствиями. Значение было выбрано равным 5,0 путем выполнения нескольких симуляций. Мы использовали это заранее определенное значение во всех симуляциях и экспериментах. Пример расчета полей показан на рисунке 9. Наконец, угол, минимизирующий общее поле, выбирается в качестве угла курса. Маленький кружок на Рисунке 9 указывает этот угол.
Этот метод имеет некоторые особенности, которые не похожи на классические методы, основанные на потенциальном поле, т.е.е., использованный Ge и Cui [26]. Во-первых, вместо того, чтобы помещать данные датчика дальности в уравнение, ODG-PF определяет препятствия (угол захвата, среднее расстояние и т. Д.) На основе данных датчика дальности, а затем вычисляет поля отталкивания препятствий. Во-вторых, поле отталкивания и поле притяжения ODG-PF являются функциями угла; то есть они не векторы. В классическом потенциальном поле направление определяется направлением полного вектора поля отталкивания и поля притяжения.Таким образом, ODG-PF очень надежен: даже если есть небольшие изменения в окружающей среде, они не так сильно влияют на траекторию. Математически основное различие между PFM и ODG-PF состоит в том, что поле притяжения и поле отталкивания (а также полное поле) являются угловыми функциями, в то время как все поля в PFM являются векторными значениями. Решение о направлении принимается путем нахождения угла с минимальным значением общего поля, а не путем вычисления арктангенса вектора.
4.Моделирование
4.1. Настройки
Положения препятствий в моделировании и на транспортном средстве были такими, как на рисунке 10. Настройки были такими же, как и в реальных экспериментах. Препятствия были расставлены зигзагообразно, и машина двигалась впереди них. Чтобы свести к минимуму влияние стены, препятствия и автомобили не располагались рядом со стенами с обеих сторон.
Мы сравнили наш новый метод ODG-PF с традиционными PFM, FGM и AFPFM. PFM и AFPFM используют искусственное потенциальное поле, и было полезно сравнить их с потенциальным полем ODG.FGM использует промежутки между препятствиями, и зависимость ODG-PF от препятствий сопоставима. Все алгоритмы, использованные в этом исследовании, определяют угол направления на основе полученных данных датчика дальности. Из данных датчика на рисунке 1 (b) мы смогли узнать, где был максимальный зазор в FGM, и рассчитать отталкивающие поля PFM, AFPFM и ODG-PF.
У каждого метода есть параметры, которые необходимо определить. Для PFM и AFPFM мы зафиксировали коэффициент поля отталкивания () равным 0,16 и провели моделирование с ними, изменяя коэффициент поля притяжения (для простоты.
Для FGM нам нужно было выбрать подходящий в (4), поэтому мы установили его на 0,5 м, что означает, что углы к цели и максимальный зазор имеют одинаковый вес при минимальном расстоянии от препятствий и транспортного средства было 0,5 м.
На самом деле, мы должны выбрать максимальное расстояние датчика для PFM и AFPFM. Наш датчик дальности может обнаруживать объект на расстоянии до 10 м, но если бы мы изменили значение в PFM и AFPFM, нам пришлось бы изменить все правила нечеткого вывода в AFPFM.Для честного сравнения мы оставили его без изменений.
Нам нужно было определить две вещи для ODG-PF. Один из них — это пороговое расстояние, которое мы установили равным 2,0 м, чтобы его можно было легко адаптировать к любым низкоскоростным датчикам с низким разрешением. Еще один параметр, который нам нужно было выбрать, был похож на PFM и AFPFM, но, как описано в (7), используется для применения штрафа, пропорционального отклонению от угла по направлению к цели. Мы установили 5.0, что было получено как в результате моделирования, так и в результате экспериментов. ODG-PF не очень чувствителен, и экспериментально его можно установить на 4.0 ~ 6.0.
, угол к цели во всех алгоритмах данного исследования, был фиксированным. То есть не было положения цели, но фиксированный угол и цель алгоритмов уклонения от препятствий в этом исследовании заключались в том, чтобы сделать все возможное, чтобы сохранить фиксированное положение, не сталкиваясь ни с чем.
Таким образом, нам нужно было изменить вектор поля притяжения, описанный в (2), на
4.2. Результаты моделирования в статической среде
Мы провели моделирование с использованием алгоритмов с теми же настройками, что и на рисунке 10, результаты которого показаны на рисунке 11.На рисунке 11 (а) показаны результаты моделирования PFM. Как и предполагалось, он сыграл ключевую роль в поиске компромисса между безопасностью и эффективностью, и PFM не работал эффективно ни в одном из случаев. Как уже говорилось в [23], PFM был очень чувствителен к отталкивающему полю, и траектории легко изменялись, даже когда транспортное средство находилось относительно далеко от препятствий. Большое значение сделало его менее чувствительным.
FGM работал лучше, чем PFM, поскольку он пытался найти самый безопасный угол, как показано на рисунке 11 (b), и имел тенденцию следовать за максимальным зазором, если транспортное средство приближалось к препятствиям, как описано в (4).В любом случае, FGM будет в опасности столкновения, если препятствие находится между углом максимального зазора и углом к воротам. AFPFM был лучше, чем PFM во всех случаях, но когда он был большим, возникали коллизии, как показано на рисунке 11 (c). Значение должно быть намного больше (для простоты в 10 раз), чем PFM. Причина этого в том, что существует коэффициент при расчете поля отталкивания, а также веса TS Fuzzy в AFPFM, которые максимум в 15 раз больше, чем в PFM, когда препятствие размещается близко к передней части транспортного средства.
Моделирование ODG-PF показало наилучшие результаты во всех случаях. Мы проводили одни и те же эксперименты несколько раз, столкновений не было. Он всегда успешно избегал препятствий, и его угол курса в конце концов вернулся к значению, как показано на Рисунке 11 (d).
PFM не дала хороших результатов, и окончательное отклонение от начальной позиции y было самым большим. Когда мы устанавливаем большое значение, отклонение становилось меньше, но, как показано на рисунке 11 (a), риск столкновения также увеличивался.
Результаты FGM были не так уж плохи. Когда мы устанавливаем меньшее значение, это вызывало коллизии, а большие значения вызывали большие отклонения.
Результаты AFPFM показывают, что он зависит от PFM, но они также показывают, что этот алгоритм можно улучшить. На рисунке 11 (c) мы можем представить себе, что существует оптимальное значение (или функция принадлежности), которое эффективно избегает препятствий без особых отклонений в моделировании, но оптимальное значение будет варьироваться в зависимости от конкретного случая.
4.3. Результаты моделирования в динамической среде
Еще одним достоинством ODG-PF является то, что он может успешно обходить препятствия без какой-либо регулировки, даже когда они движутся. Любой метод обхода препятствий не может избежать всех движущихся препятствий из-за физических ограничений транспортного средства, таких как скорость, угловая скорость, радиус вращения, диапазон измерения датчика и т. Д. Успех уклонения от движущихся препятствий в значительной степени зависит от относительной скорости между движущимся препятствием и транспортного средства, но это также зависит от алгоритма обхода препятствий.
Мы разработали три сценария движущихся препятствий. В сценариях 1 и 2 мы использовали первые два статических препятствия, использованных в предыдущих экспериментах, и движущееся препятствие, но траектория движущегося препятствия в сценарии 1 отличалась от траектории в сценарии 2.
На рисунке 12 показаны сценарии и моделирование. уклонения от движущегося препятствия в Сценариях 1 и 2. Как показано на Рисунке 12 (a), транспортное средство, использующее ODG-PF, успешно уклонилось от движущегося препятствия. Цвета транспортного средства и движущегося препятствия становились темнее по мере их сближения, а после встречи (точка, в которой они были ближе всего) их цвет снова становился белым.Используя разные цвета, читатель может легко различать движения транспортного средства и движущееся препятствие с учетом временных шагов.
В сценарии 2 движущееся препятствие приближалось с левой стороны транспортного средства с той же скоростью, что и транспортное средство (после того, как транспортное средство прошло второе статическое препятствие). Автомобиль с использованием ODG-PF двигался так, как будто он двигался вместе с препятствием.
Для более строгого сравнения алгоритмов мы разработали еще один экспериментальный сценарий.На рис. 13 (а) показаны статические препятствия, а также направление движения транспортного средства и движущегося препятствия.
Результаты моделирования этого сценария движущихся препятствий показывают, что транспортные средства с PFM, AFPFM и ODG-PF смогли избежать как статических препятствий, так и движущихся препятствий. Однако, когда мы увидели детали результатов моделирования для PFM и AFPFM, их движения были несколько нестабильными, так что транспортное средство двигалось зигзагообразно.
5. Эксперименты
5.1. Технические характеристики и настройка оборудования
На рисунке 14 показана конфигурация системы.
Используемый автомобиль представлял собой Unmanned Solution ™ ERP42v1 без тормозной системы. Его физические размеры составляли см. Датчик дальности представлял собой лазерную измерительную систему SICK ™ LMS200, которая могла определять расстояния до препятствий в диапазоне 90 ° с разрешением 0,5 °. Мы использовали Xsens ™ MTI-100 IMU для расчета угла рыскания системы с использованием алгоритма Мэджвика [27]. Во всех случаях угол рыскания в исходной точке составлял 0 °. Для записи экспериментов использовалась USB-камера Hardkernel ™ USB-CAM 720P с разрешением 640 x 480.ЦП ноутбука был Intel i5 (2 ядра, 4 потока, 2,67 ГГц) и 4 ГБ памяти. В качестве ОС использовалась Windows 7. Для реализации алгоритмов и отображения графиков использовались библиотеки Microsoft Visual C ++ и OpenCV. Все данные были записаны в реальном времени. На рисунке 15 показан снимок записанного видео. Поскольку мы реализовали все алгоритмы в одной программе для ПК, пользователь должен выбрать один из них перед запуском программы.
На рисунке показаны ① вид спереди с USB-камеры, ② данные графического датчика, ③ расчетные данные (в данном примере ODG-PF) и ④ используемые значения параметров.Таким образом, записанные видео можно использовать для анализа причины сбоя позже.
5.2. Экспериментальная среда на открытом воздухе
Эксперименты проводились в задней части зала инноваций Корейского университета. Одно препятствие состояло из двухсантиметровых ящиков из пенополистирола. В основном положения препятствий и транспортного средства были такими же, как и в экспериментах по моделированию. Наружная экспериментальная среда показана на рисунке 16.
5.3. Результаты экспериментов в статической среде
Траектория каждого эксперимента была рассчитана позже на основе сохраненных данных с использованием. Значение AFPFM изначально было установлено на 100, потому что мы использовали это значение в экспериментах в помещении.Для обычного PFM мы изначально использовали = 10 для экспериментов в помещении.
Рисунок 17 — траектории экспериментов. Временной интервал между маркерами на всех рисунках траекторий составляет 0,8 с. Скорость была установлена постоянной, но в начале каждой навигации робот разгонялся с нулевой скорости. Время выборки IMU составляет 0,01 с, и он использовался в качестве эталонных часов.
Для случаев PFM с = 10 (рисунок 17 (a)) и AFPFM с = 100 (рисунок 17 (c)) транспортное средство столкнулось со вторым препятствием.
Как это произошло при моделировании, Рисунок 17 (a) показывает, что PFM не работал хорошо и сталкивался с препятствиями, когда был большим, и отклонялся от желаемого угла, когда был маленьким. Когда он был слишком мал, он отклонился от угла цели и столкнулся со вторым препятствием, когда = 10.
Автомобиль с FGM показал себя очень хорошо, когда это необходимо для уклонения от препятствий в сложных условиях. В нескольких экспериментах столкновений не было, хотя траектория не была достигнута.
На рисунке 17 (c) показаны характеристики автомобиля с AFPFM. Когда было большим (= 100), транспортное средство столкнулось со вторым препятствием, что не имело тех же результатов, что и при моделировании, что указывает на то, что в динамической модели транспортного средства могла быть проблема. Более того, в конце эксперимента был пешеход с = 10.
ODG-PF показал лучший результат во всех случаях. Мы проводили одни и те же эксперименты несколько раз, и столкновений не было. Ему всегда удавалось избегать препятствий, как показано на Рисунке 17 (d).
Результаты экспериментов неизменно показывают, что ODG-PF эффективно и успешно обходил препятствия. Другие алгоритмы смогли избежать препятствий, но отклонения от исходного положения y были большими.
5.4. Результаты экспериментов в динамической среде
Как показано на рис. 13, мы выполнили три сценария уклонения от движущихся препятствий.
В сценариях 1 и 2 положения двух статических препятствий были такими же, как и для уклонения от статических препятствий, и мы провели эксперименты со всеми вышеупомянутыми алгоритмами.Экспериментальные результаты транспортных средств с PFM, AFPFM и FGM показывают, что их траектории не сильно отличались от траекторий для случаев статических препятствий, поскольку они находились далеко от движущегося препятствия. Как показано на рисунках 17–19, скорость мобильного робота была постоянной, за исключением начала каждого эксперимента, когда мобильный робот разгонялся с нулевой скорости до заданной скорости. Мы модернизируем ODG-PF, чтобы учесть ускорение мобильного робота в будущей работе.
В сценарии 3 мы проанализировали все алгоритмы, используя различные статические положения препятствий и сценарии.
На рисунке 18 показаны некоторые изображения из эксперимента Сценария 1 и траектория. Как при моделировании, так и в экспериментах скорость транспортного средства составляла 0,8 м / с.
Рисунок 19 показывает некоторые изображения экспериментов и траекторию для Сценария 2. Мы видим, что они также согласились с результатами моделирования, показанными на Рисунке 13 (b).
Как и в сценариях 1 и 2, мы провели эксперименты с транспортным средством и всеми вышеупомянутыми алгоритмами для перемещения препятствия в сценарии 3.Как показано на Рисунке 13 (b), весь алгоритм, кроме FGM, успешно избегал статических и движущихся препятствий при моделировании. Этот сценарий является суровым, потому что в конце экспериментов зазор между статическим препятствием и движущимся препятствием был лишь немного шире, чем ширина транспортного средства. При моделировании мы отметили, что все алгоритмы успешно преодолели разрыв, когда он был относительно большим. Мы сократили разрыв в симуляциях до такой степени, что один из них начал двигаться по-другому.На Рисунке 13 (b) транспортное средство с FGM подошло к максимальному зазору, который находился слева от транспортного средства, когда оно начало движение. Мы также проводили эксперименты с большим разрывом, при котором все алгоритмы работали хорошо.
На рисунке 20 показаны некоторые изображения и траектории экспериментов по сценарию 3. В результатах, отличных от моделирования, только ODG-PF успешно прошел через промежуток между статическими препятствиями и движущимися препятствиями. Причины успеха и неудачи обсуждаются позже.
Для PFM и AFPFM направление определяется значением арктангенса полного вектора поля. Как описано в (1), полное поле представляет собой сумму поля притяжения и поля отталкивания. Отталкивающее поле становится больше, когда расстояние до препятствий становится меньше. В определенный момент поле отталкивания начинает подавлять поле притяжения, и значение арктангенса направляет автомобиль назад. Мы проанализировали причину сбоя, которая объясняется в следующем разделе.Мобильный робот не смог резко изменить направление, что привело к столкновению.
Тем не менее, автомобиль избегал статических и движущихся препятствий близко, но успешно с ODG-PF. Гауссово отталкивающее поле ODG-PF эффективно описывает препятствия и не пропускает их.
На рисунке 20 (d) показаны траектории транспортного средства с использованием различных алгоритмов обхода препятствий. Помимо случая ODG-PF, экспериментальные результаты не совпадали с результатами моделирования, и поэтому мы думаем, что в модели транспортного средства, использованной в моделировании, могли быть некоторые ошибки.
Экспериментальная траектория FGM отличалась от траектории моделирования, что, как мы думаем, связано с моделью транспортного средства. Как и в результате моделирования, показанном на рисунке 13 (b), FGM пыталась следовать максимальному зазору.
5.5. Оценка и обсуждение
Чтобы оценить результаты различных алгоритмов, мы должны рассмотреть, столкнулся ли автомобиль с каждым алгоритмом с какими-либо препятствиями или нет. Если транспортное средство с определенным алгоритмом не столкнулось с какими-либо препятствиями, мы должны оценить алгоритм по некоторым критериям.При рассмотрении эффективности (изображенной на рисунке 21) максимальное отклонение от начальной направляющей линии может быть хорошим критерием.
Таблица 1 содержит результаты коллизий и максимальное отклонение от начальной строки для каждого алгоритма. Избегать препятствий важнее эффективности, потому что это вопрос безопасности. Эффективность имеет значение только в том случае, если нет столкновений с препятствиями.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

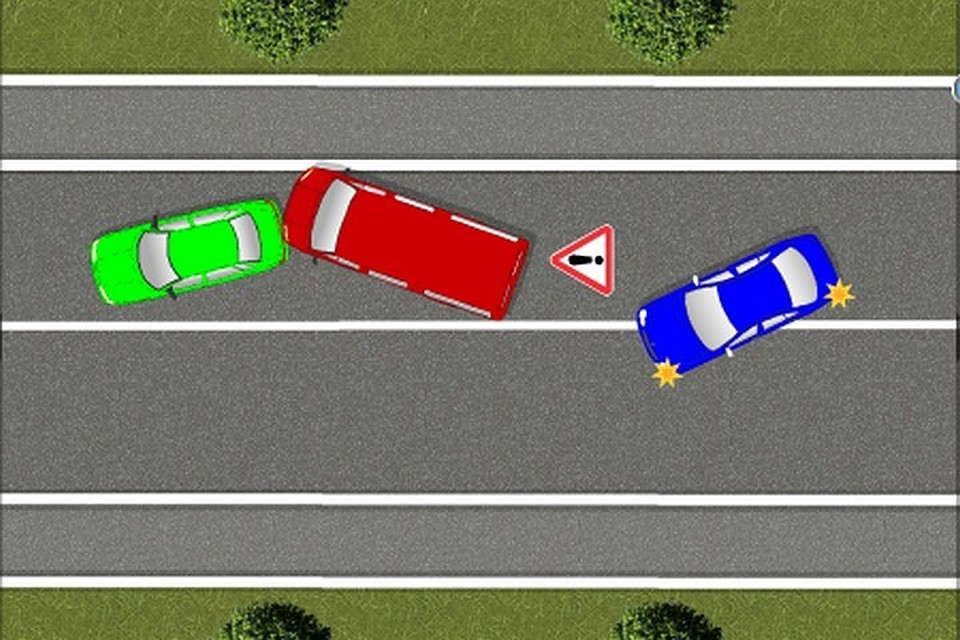 Специалист свяжется с вами в день доставки, чтобы уточнить время и заранее подготовить сдачу с любой купюры. Вы подписываете товаросопроводительные документы, вносите денежные средства, получаете товар и чек.
Специалист свяжется с вами в день доставки, чтобы уточнить время и заранее подготовить сдачу с любой купюры. Вы подписываете товаросопроводительные документы, вносите денежные средства, получаете товар и чек. 00 до 19.00. Когда товар поступит на склад в Ростове-на-Дону, курьерская служба свяжется для уточнения деталей. Специалист предложит выбрать удобное время доставки и уточнит адрес. Осмотрите упаковку на целостность и соответствие указанной комплектации.
00 до 19.00. Когда товар поступит на склад в Ростове-на-Дону, курьерская служба свяжется для уточнения деталей. Специалист предложит выбрать удобное время доставки и уточнит адрес. Осмотрите упаковку на целостность и соответствие указанной комплектации.