Устройство кривошипно-шатунного механизма
Основной задачей двигателей внутреннего сгорания, использующиеся на всевозможной технике, является преобразование энергии, которая выделяется при сжигании определенных веществ, в случае с ДВС – это топливо на основе нефтепродуктов или спиртов и воздуха, необходимого для горения.
Преобразование энергии производится в механическое действие – вращение вала. Далее уже это вращение передается дальше, для выполнения полезного действия.
Однако реализация всего этого процесса не такая уж и простая. Нужно организовать правильно преобразование выделяемой энергии, обеспечить подачу топлива в камеры, где производиться сжигание топливной смеси для выделения энергии, отвод продуктов горения. И это не считая того, что тепло, выделяемое при сгорании нужно куда-то отводить, нужно убрать трение между подвижными элементами. В общем, процесс преобразования энергии сложен.
Поэтому ДВС – устройство довольно сложное, состоящее из значительного количества механизмов, выполняющих определенные функции.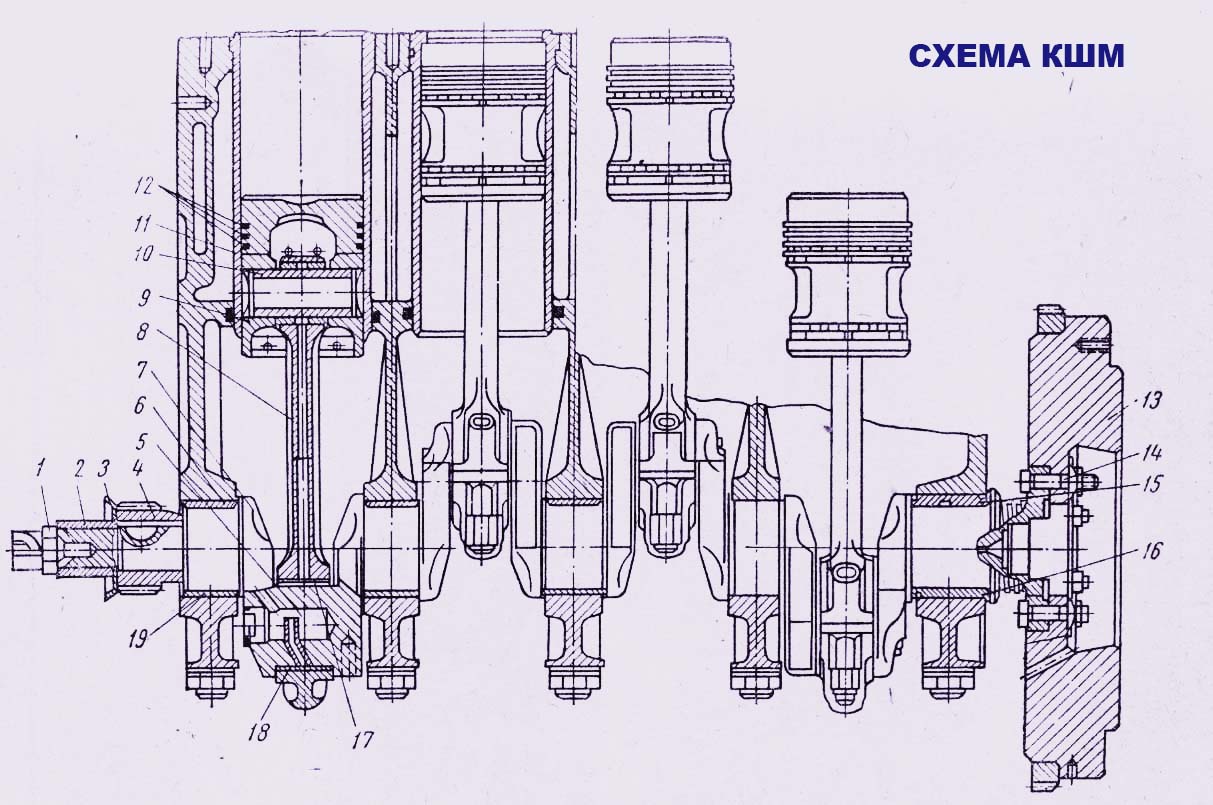
Принцип действия кривошипно-шатунного механизма
Основная же задача лежит на этом механизме, ведь он преобразовывает возвратно-поступательное перемещение поршня во вращение коленчатого вала, того вала, от движения которого и производится полезное действие.
Устройство КШМ
Чтобы было более понятно, в двигателе есть цилиндро-поршневая группа, состоящая из гильз и поршней. Сверху гильза закрыта головкой, а внутри ее помещен поршень. Закрытая полость гильзы и является пространством, где производится сгорание топливной смеси.
При сгорании объем горючей смеси значительно возрастает, а поскольку стенки гильзы и головка являются неподвижными, то увеличение объема воздействует на единственный подвижный элемент этой схемы – поршень.
И вот далее уже в действие вступает кривошипно-шатунный механизм. Поршень связан с кривошипом вала посредством шатуна. Данное соединение является жестким, но подвижным. Сам поршень закреплен на шатуне посредством пальца, что позволяет легко шатуну менять положение относительно поршня.
Шатун же своей нижней частью охватывает шейку кривошипа, которая имеет цилиндрическую форму. Это позволяет менять угол между поршнем и шатуном, а также шатуном и кривошипом вала, но при этом смещаться шатун вбок не может. Относительно поршня он только меняет угол, а на шейке кривошипа он вращается.
Поскольку соединение жесткое, то расстояние между шейкой кривошипа и самим поршнем не изменяется. Но кривошип имеет П-образную форму, поэтому относительно оси коленвала, на которой размещен этот кривошип, расстояние между поршнем и самим валом меняется.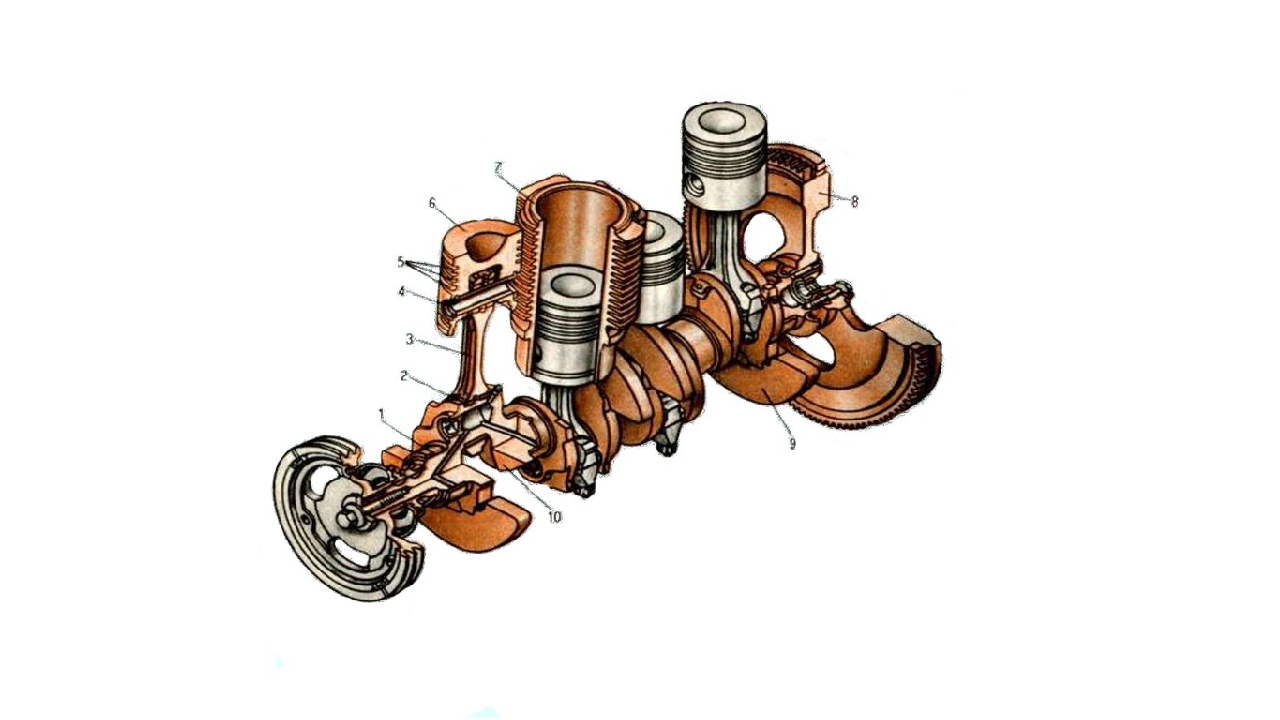
За счет применения кривошипов и удалось организовать преобразование перемещения поршня во вращение вала.
Но это схема взаимодействия только цилиндро-поршневой группы с кривошипно-шатунным механизмом.
На деле же все значительно сложнее, ведь имеются взаимодействия между элементами этих составляющих, причем механические, а это значит, что в местах контакта этих элементов будет возникать трение, которое нужно по максимуму снизить. Также следует учитывать, что один кривошип неспособен взаимодействовать с большим количеством шатунов, а ведь двигатели создаются и с большим количеством цилиндров – до 16. При этом нужно же и обеспечить передачу вращательного движения дальше. Поэтому рассмотрим, из чего состоит цилиндро-поршневая группа (ЦПГ) и кривошипно-шатунный механизм (КШМ).
Начнем с ЦПГ. Основными в ней являются гильзы и поршни. Сюда же входят и кольца с пальцами.
Гильза
Съёмная гильза
Гильзы существуют двух типов – сделанные непосредственно в блоке и являющиеся их частью, и съемные. Что касается выполненных в блоке, то представляют они собой цилиндрические углубления в нем нужной высоты и диаметра.
Что касается выполненных в блоке, то представляют они собой цилиндрические углубления в нем нужной высоты и диаметра.
Съемные же имеют тоже цилиндрическую форму, но с торцов они открыты. Зачастую для надежной посадки в свое посадочное место в блоке, в верхней части ее имеется небольшой отлив, обеспечивающий это. В нижней же части для плотности используются резиновые кольца, установленные в проточные канавки на гильзе.
Внутренняя поверхность гильзы называется зеркалом, потому что она имеет высокую степень обработки, чтобы обеспечить минимально возможное трение между поршнем и зеркалом.
В двухтактных двигателях в гильзе проделываются на определенном уровне несколько отверстий, которые называются окнами. В классической схеме ДВС используется три окна – для впуска, выпуска и перепуска топливной смеси и отработанных продуктов. В оппозитных же установках типа ОРОС, которые тоже являются двухтактными, надобности в перепускном окне нет.
Поршень
Поршень принимает на себя энергию, выделяемую при сгорании, и за счет своего перемещения преобразовывает ее в механическое действие.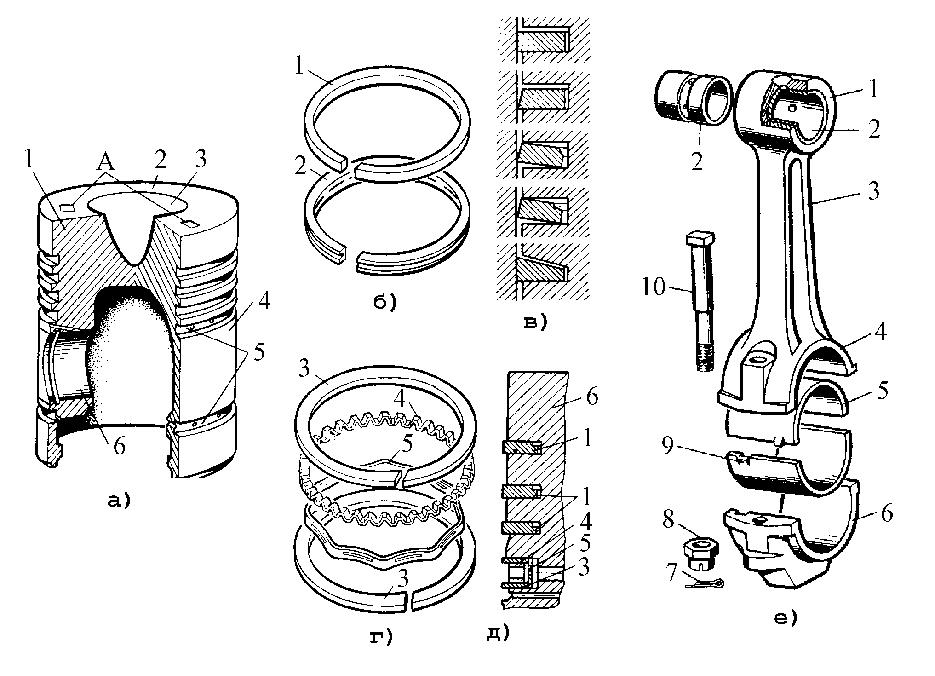 Состоит он из днища, юбки и бобышек для установки пальца.
Состоит он из днища, юбки и бобышек для установки пальца.
Устройство поршня
Именно днищем поршень и воспринимает энергию. Поверхность днища в бензиновых моторах изначально была ровной, позже на ней стали делать углубления для клапанов, предотвращающих столкновение последних с поршнями.
В дизельных же моторах, где смесеобразование происходит непосредственно в цилиндре, и составляющие смеси туда подаются по отдельности, в днищах поршня выполнена камера сгорания – углубления особой формы, обеспечивающие более лучшее смешивание компонентов смеси.
Отличие дизельного двигателя от бензиновогоВ инжекторных бензиновых двигателях тоже стали применять камеры сгорания, поскольку в них тоже составные части смеси подаются по отдельности.
Юбка является лишь его направляющей в гильзе. При этом нижняя часть ее имеет особую форму, чтобы исключить возможность соприкосновения юбки с шатуном.
Чтобы исключить просачивание продуктов горения в подпоршневое пространство используются поршневые кольца.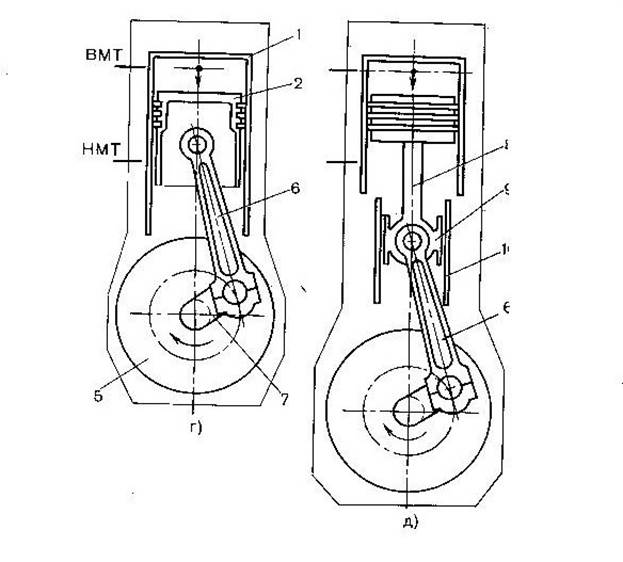 Они подразделяются на компрессионные и маслосъемные.
Они подразделяются на компрессионные и маслосъемные.
В задачу компрессионных входит исключение появления зазора между поршнем и зеркалом, тем самым сохраняется давление в надпоршневом пространстве, которое тоже участвует в процессе.
Если бы компрессионных колец не было, трение между разными металлами, из которых изготавливаются поршень и гильза было бы очень высоким, при этом износ поршня происходил бы очень быстро.
В двухтактных двигателях маслосъемные кольца не применяются, поскольку смазка зеркала производиться маслом, которое добавляется в топливо.
В четырехтактных смазка производится отдельной системой, поэтому чтобы исключить перерасход масла используются маслосъемные кольца, снимающие излишки его с зеркала, и сбрасывая в поддон. Все кольца размещаются в канавках, проделанных в поршне.
Бобышки – отверстия в поршне, куда вставляется палец. Имеют отливы с внутренней части поршня для увеличения жесткости конструкции.
Палец представляет собой трубку значительной толщины с высокоточной обработкой внешней поверхности.
Это конструкция ЦПГ. Теперь рассмотрим устройство кривошипно-шатунного механизма.
Шатун
Итак, состоит он из шатуна, коленчатого вала, посадочных мест этого вала в блоке и крышек крепления, вкладышей, втулки, полуколец.
Шатун – это стержень с отверстием в верхней части под поршневой палец. Нижняя часть его сделана в виде полукольца, которым он садится на шейку кривошипа, вокруг шейки он фиксируется крышкой, внутренняя поверхность ее тоже выполнена в виде полукольца, вместе с шатуном они и формируют жесткое, но подвижное соединение с шейкой – шатун может вращаться вокруг ее. Соединяется шатун со своей крышкой посредством болтовых соединений.
Чтобы снизить трение между пальцем и отверстием шатуна применяется медная или латунная втулка.
По всей длине внутри шатун имеет отверстие, через которое масло подается для смазки соединения шатуна и пальца.
Коленчатый вал
Перейдем к коленчатому валу. Он имеет достаточно сложную форму. Осью его выступают коренные шейки, посредством которых он соединен с блоком цилиндров. Для обеспечения жесткого соединения, но опять же подвижного, в блоке посадочные места вала выполнены в виде полуколец, второй частью этих полуколец выступают крышки, которыми вал поджимается к блоку. Крышки к с блоком соединены болтами.
Коленвал 4-х цилиндрового двигателя
Коренные шейки вала соединены с щеками, которые являются одной из составных частей кривошипа. В верхней части этих щек располагается шатунная шейка.
Количество коренных и шатунных шеек зависит от количества цилиндров, а также их компоновки. В рядных и V-образных двигателях на вал передаются очень большие нагрузки, поэтому должно быть обеспечено крепление вала к блоку, способное правильно распределять эту нагрузку.
Для этого на один кривошип вала должно приходиться две коренные шейки. Но поскольку кривошип размещен между двух шеек, то одна из них будет играть роль опорной и для другого кривошипа. Из этого следует, что у рядного 4-цилиндрового двигателя на валу имеется 4 кривошипа и 5 коренных шеек.
Из этого следует, что у рядного 4-цилиндрового двигателя на валу имеется 4 кривошипа и 5 коренных шеек.
У V-образных двигателей ситуация несколько иная. В них цилиндры расположены в два ряда под определенным углом. Поэтому один кривошип взаимодействует с двумя шатунами. Поэтому у 8-цилиндрового двигателя используется только 4 кривошипа, и опять же 5 коренных шеек.
Уменьшение трения между шатунами и шейками, а также блоком с коренными шейками достигается благодаря использованию вкладышей – подшипников трения, которые помещаются между шейкой и шатуном или блоком с крышкой.
Смазка шеек вала производится под давлением. Для подачи масла применяются каналы, проделанные в шатунных и коренных шейках, их крышках, а также вкладышах.
В процессе работы возникают силы, которые пытаются сместить коленчатый вал в продольном направлении. Чтобы исключить это используются опорные полукольца.
В дизельных двигателях для компенсации нагрузок используются противовесы, которые прикрепляются к щекам кривошипов.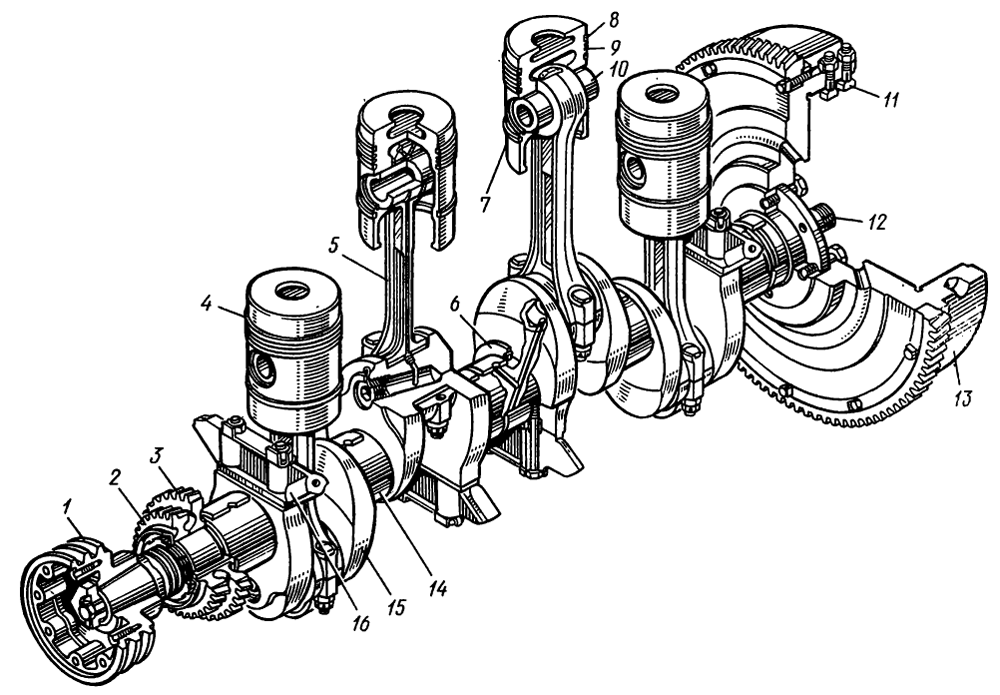
Маховик
С одной из сторон вала сделан фланец, к которому прикрепляется маховик, выполняющий несколько функций одновременно. Именно от маховика передается вращение. Он имеет значительный вес и габариты, что облегчает вращение коленчатому валу после того, как маховик раскрутится. Чтобы запустить двигатель нужно создать значительное усилие, поэтому по окружности на маховик нанесены зубья, которые называются венцом маховика. Посредством этого венца стартер раскручивает коленчатый вал при запуске силовой установки. Именно к маховику присоединяются механизмы, которые и используют вращение вала на выполнение полезного действия. У автомобиля это трансмиссия, обеспечивающая передачу вращения на колёса.
Чтобы исключить осевые биения, коленчатый вал и маховик должны быть хорошо отбалансированы.
Другой конец коленчатого вала, противоположный фланцу маховика используется зачастую для привода остальных механизмом и систем мотора: к примеру, там может размещаться шестерня привода масляного насоса, посадочное место для приводного шкива.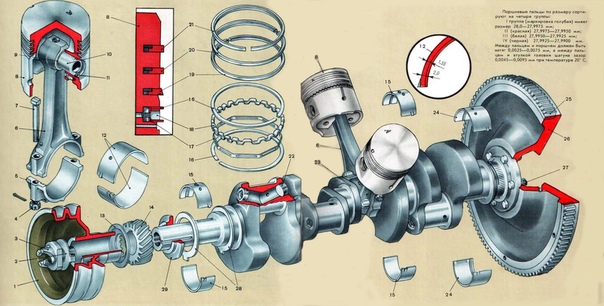
Это основная схема коленчатого вала. Особо нового пока ничего не придумано. Все новые разработки направлены пока только на снижение потерь мощности в результате трения между элементами ЦПГ и КШМ.
Также стараются снизить нагрузку на коленчатый вал путем изменения углов положения кривошипов относительно друг друга, но особо значительных результатов пока нет.
Работа кривошипно-шатунного механизма
Как авторитетно свидетельствуют историки техники, еще за много лет до того, как появился самый первый автомобиль, был изобретен кривошипно-шатунный механизм. Когда именно произошло это событие, пока не установлено, зато точно известно, что эти конструкции активно использовались в таких машинах, как швейные, паровозы, а также штамповочные прессы.
Еще задолго до того, как был изобретен двигатель внутреннего сгорания, задача преобразования возвратно-поступательного движения в движение вращательное была весьма актуальна. Например, без ее эффективного решения не могла функционировать паровая машина, которая послужила настоящим «локомотивом» промышленной революции. Способ преобразования движения поршней во вращение был изобретен еще в средине XVIII века, и именно он был взят за основу двигателей внутреннего сгорания.
Способ преобразования движения поршней во вращение был изобретен еще в средине XVIII века, и именно он был взят за основу двигателей внутреннего сгорания.
Интересно, что с тех пор, как появились первые ДВС, прошло уже очень немало времени. Они претерпели массу изменений, однако кривошипно-шатунный механизм в них остался практически таким же, как и был изначально.
Что касается принципа его действия, то он основан на том, что некие детали (а именно – поршни), с помощью шарниров соединяются с некоторыми частями вала, представляющими собой его «ступени». Сами поршни совершают возвратно-поступательные движения, благодаря чему оказывают соответствующие механические нагрузки на «колена» вала. Последний в результате этого совершает вращательное движение.
Таким образом, та задача, которую решет кривошипно-шатунный механизм, состоит в том, чтобы возвратно-поступательное движение поршней преобразовать во вращательное движение коленчатого вала. Что касается конструкции, то все детали кривошипно-шатунного механизма можно разделить на две категории: неподвижные подвижные.
Что касается конструкции, то все детали кривошипно-шатунного механизма можно разделить на две категории: неподвижные подвижные.
К разряду неподвижных относятся блоки цилиндров, поддоны, прокладки и головки. Подвижными частями являются сами поршни с установленными на них кольцами, маховики, коленчатые валы, а также шатуны. И подвижные, и неподвижные составляющие кривошипно-шатунного механизма имеют в своей конструкции различные крепежные детали.
Шатун и коленчатый вал
Роль шатуна состоит в том, чтобы обеспечивать трансляцию того усилия, которое обеспечивает поршень, коленчатому валу, причем как при рабочем, так и при обратном ходе во время вспомогательных тактов. Его составными частями являются стержень двутаврового сечения, верхняя головка и разъемная нижняя головка, которая закрепляется на шатунной шейке коленчатого вала. Материалом для изготовления шатуна и крышки является углеродистая или легированная сталь. В конструкции верхней головки шатуна содержится одна или две втулки, которые в нее запрессовываются и изготавливаются из такого материала, как оловянистая бронза. В нижней головке шатуна наличествуют вкладыши, изготавливаемые из тонкого стального листа, причем они заливаются слоем антифрикционного сплава.
В нижней головке шатуна наличествуют вкладыши, изготавливаемые из тонкого стального листа, причем они заливаются слоем антифрикционного сплава.
Между собой верхняя и нижняя головки шатуна соединяются парой болтов и гаек, причем для обеспечения надежности фиксации они или снабжаются контргайками, или же шплинтуются.
Коленвал, который воспринимает оказываемые на него усилия поршней посредством шатунов, преобразует их во вращение. На нем располагаются шатунные и коренные шейки, противовесы, фланец, маховик. На коленчатых валах некоторых двигателей внутреннего сгорания устанавливается также храповик. Кроме того, на коленвалах монтируются шкивы приводов вентилятора и водяного насоса.
Коленчатые валы двигателей современных автомобилей вращаются со скоростью от 3000 до 6000 оборотов в минуту. Поэтому коренные подшипники, в которых они закрепляются, испытывают ускоренный износ. Чтобы его уменьшить, применяются специальные противовесы.
детали и запчасти КШМ двигателя
Подобрать запчасти в каталоге «Кривошипношатунный механизм»
Основные компоненты и принцип работы КШМ
Состоит кривошипно-шатунный механизм из таких подвижных деталей и элементов крепежа, как:
- Коленвал
- Поршни с поршневыми кольцами и пальцами
- Шатуны
- Вкладыши, втулки
- Стопорное кольцо
- Крышки
Недвижимыми составляющими данного устройства считаются цилиндры, ГБЦ, блок цилиндров, картер, поддон, прокладка ГБЦ.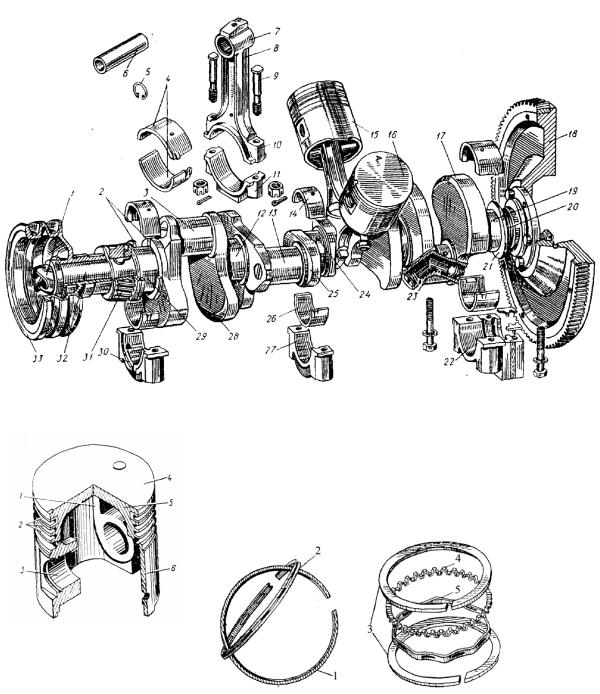
В процессе загорания топливно-горючей смеси, оказавшиеся в цилиндрах газы, перемещают поршень в нижнее положение. Благодаря поршневому кольцу шатун может прокручиваться, компенсируя момент прокручивания коленвала при нахождении поршня вверху.
Противовесы не позволяют коленвалу повернуться, поэтому крутящий момент на него подают газы, проходящие сквозь шатун и поршень. Вращают колено латунные подшипники скольжения или шатунные вкладыши. В результате коленвал передает усилие на коробку передач и колеса.
Компрессионные кольца предназначены для обеспечения герметичного состояния и необходимой компрессии в камере сгорания. Для предотвращения проникновения внутрь смазки установлено маслосъемное кольцо, которое снимает остатки масел со стенок цилиндра.
Неисправности кривошипно-шатунного механизма
Так как данный механизм эксплуатируется в чрезвычайно тяжелых условиях при повышенной температуре на высоких скоростных режимах, именно он повреждается первым в системе двигателя. Если возникают неисправности в этом узле, они часто приводят к дорогостоящему ремонту мотора.
Если возникают неисправности в этом узле, они часто приводят к дорогостоящему ремонту мотора.
Причиной неполадок обычно является естественный износ компонентов силового агрегата или нарушение правил его эксплуатации. При несвоевременном проведении техобслуживания, применении низкосортных смазочных материалов, топлива, фильтров, продолжительной эксплуатации перегруженного транспортного средства преждевременно могут возникнуть проблемы в работе кривошипно-шатунного механизма.
Типичными неполадками данного узла считаются:- Изнашивание коренных и шатунных подшипников. Такое повреждение сопровождается приглушенным стуком в блоке цилиндров, который отчетливо слышен при повышении оборотов, также падает давление масла в системе. В подобном случае эксплуатация автотранспортного средства запрещена
- Изнашивание поршней и цилиндров, которое сопровождается звонким гулом при работе непрогретого мотора и возникновением синеватого дыма из выхлопной трубы
- Изнашивание поршневых пальцев.
 Для данной проблемы характерен звонкий стук вверху блока цилиндров при работающем моторе
Для данной проблемы характерен звонкий стук вверху блока цилиндров при работающем моторе - Повреждение и залегание поршневых колец. Оно проявляется перебоями в работе силового агрегата, падением компрессии, повышением расхода масла и появлением синего дыма из выхлопа
Кроме этого со временем на поршнях и на стенках камеры сгорания может появляться нагар, который приводит к сильному нагреванию двигателя, увеличенному расходу топлива и понижению мощности авто.
Чтобы максимально продлить срок службы кривошипно-шатунного механизма следует постоянно контролировать крепления, при необходимости подтягивать болты на картере и ГБЦ, а также содержать мотор в чистоте и периодически удалять нагар, который образуется в камере сгорания.
Кривошипно шатунный механизм. Назначение и его главная миссия
Приветствую читателей нашего уютного блога! Сейчас поговорим о сердце наших железных коней, двигателях внутреннего сгорания. А если точнее, кривошипно шатунный механизм – один из ключевых механизмов мотора.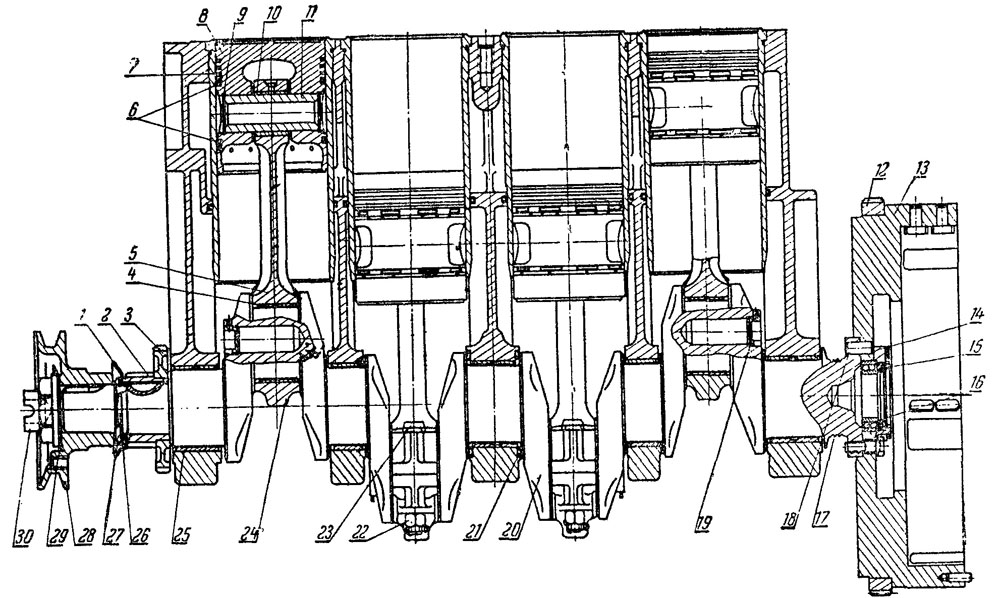
Трудно переоценить назначение кривошипно шатунного механизма. По сути, именно его мы обязаны благодарить за то, что наши железные кони не стоят на месте, а могут перевозить наши бренные тела и дарить нам радость вождения.
Если говорить сухим техническим языком, то назначение КШМ предназначено для преобразования энергии сгоревшей топливно-воздушной смеси в механическое вращение.
Естественно, кривошипно шатунный механизм не монолитная конструкция и состоит из ряда более простых деталей, о которых пойдёт речь ниже.
Кривошипно шатунный механизм: дьявол кроется в деталях
Условно элементы кривошипно-шатунного механизма можно разделить на две большие подгруппы: подвижные и неподвижные части.
К первой относятся поршни с кольцами и пальцами, шатуны, коленчатый вал (в простонародье коленвал), а также маховик.
Блок цилиндров
Неподвижные элементы КШМ представлены блоком цилиндров и головкой блока цилиндров, картером, а также прокладкой, расположенной между блоком и головкой.
Поршень
А теперь чуточку подробнее о роли каждого из актёров театра кривошипно шатунного механизма. Одним из первых удар сгорающей топливно-воздушной смеси принимает на себя поршень.
Этот героический элемент представляет собой металлическую цилиндрическую деталь, грубо говоря, имеющую форму стакана.
На самом деле его форма довольно непростая – с канавками, выпуклостями, отверстиями и вырезами.
Все эти сложности форм нужны не только для эффективной работы мотора. Чтобы было где разместить поршневые кольца, а также куда вставить поршневой палец, к которому крепится следующая важная деталь механизма – шатун.
Шатун
Смысл существования шатуна прост, как пять копеек — передача поступательного движения поршня коленчатому валу.
Довольно скучная, но важная роль. Сам по себе шатун выглядит как металлический стержень двутаврового сечения.
С одного его конца находится отверстие для крепления к поршню при помощи поршневого пальца, а с другого – полукольцо, которое надевается на шатунную шейку вала и фиксируется болтовыми соединениями специальной крышкой.
Стоит отметить, что соединение шатуна с коленвалом подвижное – он же должен вращаться.
Коленчатый вал
Важность следующего элемента КШМ сложно переоценить – это коленчатый вал.
Конечно, назвать эту деталь валом в привычном понимании довольно трудно – форма у него сложная и всё из-за того, что к нему крепятся все шатунно-поршневые связки двигателя.
Коленвал — ключевой вращающий элемент мотора и ему приходится выдерживать невероятные нагрузки, поэтому и требования к качеству его исполнения и прочности материалов высочайшие.
Основными деталями коленчатого вала являются шатунные шейки (места, куда крепятся шатуны), щёки, коренные шейки и противовесы.
Кстати, своё название кривошипно шатунный механизм получил именно благодаря части коленвала. Если быть точным, кривошипу – так иногда называют связку шатунной шейки и щёк по обе стороны от неё.
Маховик
Венчает коленчатый вал с одной из сторон маховик.
Нужно отметить, что, несмотря на свою относительную внешнюю простоту, маховик играет сразу несколько ролей.
Во-первых, в его главную задачу входит поддержание равномерного вращения коленвала во время работы мотора.
Во-вторых, именно это скромное металлическое колесо выступает связующим звеном между стартером и коленчатым валом, когда Вы поворачиваете ключ зажигания для запуска двигателя.
Практически все подвижные части кривошипно шатунного механизма располагаются в блоке цилиндров. А закрывает всё это крутящееся и вращающееся безобразие от наших с Вами глаз головка блока цилиндров.
В неё, как правило, встроены клапаны, свечи и каналы для подвода охлаждающей жидкости, масла, а также воздушно-топливной смеси.
Нужно отметить, что именно блок цилиндров вместе с головкой обуславливают такой немаловажный параметр двигателя, как его масса.
В классическом исполнении эти элементы изготавливаются из чугуна, но, благодаря современным технологиям, автопроизводители всё чаще применяют алюминий в их конструкции, что благотворно влияет на вес мотора и, как следствие, всего автомобиля.
Применение лёгких сплавов стало возможным даже в столь критичном элементе блока. Гильзы цилиндров (в них перемещаются поршни), должны обладать стойкостью к износу и выдерживать высокие температуры.
А сколько цилиндров у твоего коня?
В заключение, дорогие наши читатели, хотелось бы сказать несколько слов о видах компоновки двигателей внутреннего сгорания и схемах расположения цилиндров.
Автомобильные концерны комплектуют свои творения моторами нескольких видов, а именно:
- рядными;
- V-образными;
- оппозитными;
- W-образными.
С точки зрения баланса, самыми оптимальными являются рядные и оппозитные двигатели.
Первые довольно распространены в автомире – рядные четырёхцилиндровые агрегаты встречаются сплошь и рядом. А вот судьба оппозитных не столь публична, они стали синонимом некой эксклюзивности и «клубности».
Так, к примеру, их можно встретить в недрах спортивных Porsche или Subaru.
Оптимальным же сочетанием характеристик обладают V-образные и их родственные W-образные двигатели. На их базе строят как доступные для среднестатистического автолюбителя машины, так и сумасшедшие суперкары, стоимость которых столь же невероятна, как и характер.
На их базе строят как доступные для среднестатистического автолюбителя машины, так и сумасшедшие суперкары, стоимость которых столь же невероятна, как и характер.
Работа W-образного двигателя:
Уважаемые посетители блога, в этой небольшой статье мы попытались прояснить назначение кривошипно шатунного механизма, рассмотреть его в общих чертах его компоненты.
Читайте статьи на блоге и повышайте свой профессиональный уровень.
Кривошипно-шатунный механизм (КШМ). Маятник Капицы » РобоВики
Данная статья является вводной теорией к занятию по робототехнике «Кривошипно-шатунный механизм из Lego EV3″
Первые КШМПервые упоминания об использовании кривошипно-шатунного механизма можно отнести ко временам Древнего Рима (примерно III век н.э.). Машина для распиливания каменных блоков передавала вращение от водяного колеса с помощью зубчатой передачи на кривошипно-шатунный механизм, который преобразовывал вращательное движение в возвратно-поступательное движение полотна пилы. Также такие устройства могли использоваться на древних лесопилках.
Также такие устройства могли использоваться на древних лесопилках.
Большого распространения такие машины не получили – деревянные части из-за большого количества трущихся деталей быстро изнашивались и требовали частого ремонта, а рабский труд был намного дешевле и не требовал большой квалификации рабочих.
В XVI веке кривошипно-шатунный механизм появился на деревянных самопрялках. Самопрялка – это ручной станок для прядения нити из шерсти, состоящий из двух катушек. В самопрялке для скручивания нити использовался принцип ременной передачи. Раньше большую катушку приходилось раскручивать рукой. К самопрялке добавили педаль. Нажимая ногой на педаль, работник смог раскручивать катушку без использования рук. Этот механизм упростил работу и позволил за то же время производить больше пряжи. В данном устройстве возвратно-поступательное движение педали передавалось через деревянный шатун на кривошип и преобразовывалось во вращательное движение большой катушки (шкива).
КШМ в паровых машинах
Начиная с начала XVIII века большую популярность среди изобретателей и ученых начинают получать паровые машины. Первый паровой двигатель для водяного насоса построил в 1705 году английский изобретатель Томас Ньюкомен для выкачивания воды из глубоких шахт.
Позднее устройство парового двигателя было усовершенствовано шотландским инженером и механиком Джеймсом Уаттом (1736-1819). Кстати, именно Джеймс Уатт ввел в оборот термин «лошадиная сила», а его именем назвали единицу мощности Ватт. Паровая машина Уатта получила сложную систему связанных тяг, а планетарная зубчатая передача преобразовывала возвратно-поступательное движение поршня во вращательное движение маховика (большого тяжелого колеса).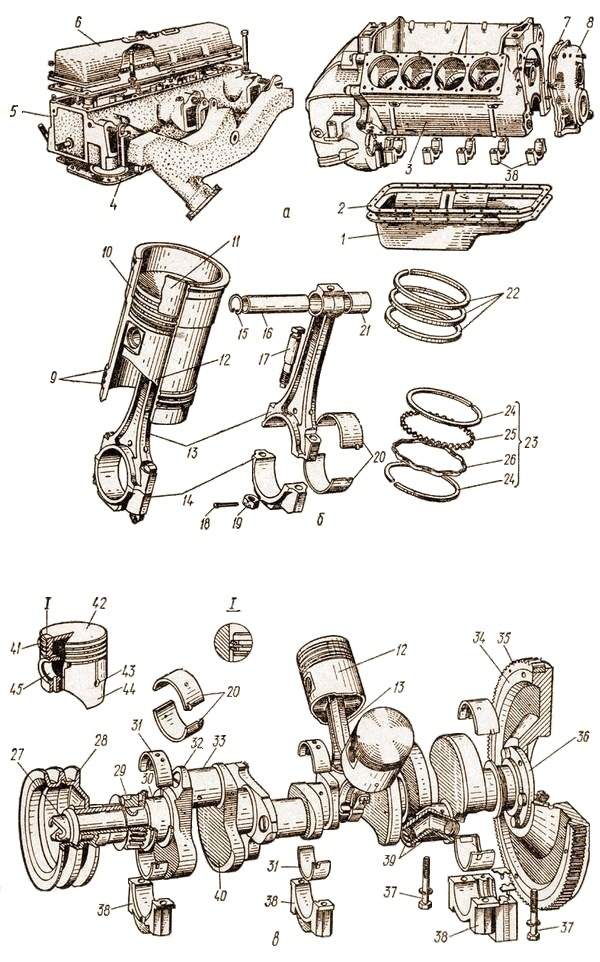 Данная паровая машина стала универсальной, так как в отличие от машины Ньюкомена поршень имел рабочий ход в обе стороны. Машина Уатта получила широкое распространение на ткацких фабриках, в металлургии, при строительстве первых паровозов для железных дорог XVIII века.
Данная паровая машина стала универсальной, так как в отличие от машины Ньюкомена поршень имел рабочий ход в обе стороны. Машина Уатта получила широкое распространение на ткацких фабриках, в металлургии, при строительстве первых паровозов для железных дорог XVIII века.
Нужно сказать, что паровыми машинами занимались в те времена очень многие изобретатели. Так, в Российской Империи свою двухцилиндровую паровую машину изобрел инженер Иван Иванович Ползунов (1728-1766).
В XIX веке паровую машину Уатта упростили, заменив сложный планетарный механизм на кривошипно-шатунный механизм.
Паровая машина с кривошипно-шатунным механизмомСхема паровой машины с кривошипно-шатунным механизмомПаровая машина с КШМ нашла широкое применение при строительстве первых автомобилей на паровой тяге и паровозов, перевозящих грузы по железной дороге.
ПаровозКШМ в двигателях внутреннего сгоранияДо этого мы рассматривали использование кривошипно-шатунного механизма в паровых двигателях. В паровом двигателе топливо сгорает в печи (вне цилиндра) и нагревает водяной котел, и уже водяной пар в цилиндре толкает поршень.
В паровом двигателе топливо сгорает в печи (вне цилиндра) и нагревает водяной котел, и уже водяной пар в цилиндре толкает поршень.
В двигателе внутреннего сгорания топливная смесь (воздух + газ, или воздух + бензин и т.д.) поджигается внутри цилиндра и продукты горения толкают поршень. Сокращенно такие двигатели называют ДВС.
Первый одноцилиндровый ДВС на газовом топливе построил в 1860 году в Париже французский изобретатель Жан Ленуар.
Двигатель внутреннего сгорания Жана Ленуара (внешне очень похож на паровую машину)Однако широкое применение двигатели внутреннего сгорания нашли в конце XIX века после получения керосина и бензина из нефти. Появление жидкого топлива позволило создать экономичные двигатели небольшой массы, которые можно было использовать для привода транспортных машин.
В 1881-1885 гг. российский изобретатель Огнеслав Костович сконструировал и построил в России восьмицилиндровый двигатель мощностью 59 кВт.
Двигатель внутреннего сгорания Огнеслава КостовичаВ 1897 г. немецким инженером Рудольфом Дизелем был спроектирован и построен первый двигатель с воспламенением от сжатия. Это был компрессорный двигатель, работающий на керосине, впрыскиваемом в цилиндр при помощи сжатого воздуха.
немецким инженером Рудольфом Дизелем был спроектирован и построен первый двигатель с воспламенением от сжатия. Это был компрессорный двигатель, работающий на керосине, впрыскиваемом в цилиндр при помощи сжатого воздуха.
Все эти ДВС имели схожие черты и использовали кривошипно-шатунный механизм для преобразования возвратно-поступательного движения поршня во вращательное движение коленвала.
Давайте посмотрим на схему устройства современного двигателя внутреннего сгорания.
Схема кривошипно-шатунного механизма в двигателе внутреннего сгоранияОбщие определения:
Поршень совершает возвратно-поступательное движение вдоль цилиндра – он ходит вверх и вниз.
Шатун – деталь, связывающая кривошип и поршень.
Кривошип – условная деталь, которая связывает шатун с коленвалом.
Противовес снижает вибрации при вращении коленвала.
Блок цилиндров – корпус, в котором находятся цилиндры двигателя.
Поршневой палец – цилиндрическая деталь, ось вращения шатуна относительно поршня.
Коленвал (коленчатый вал) – ось вращения ступенчатой формы.
Верхняя мертвая точка – крайнее верхнее положение поршня, где меняется направление его движения.
Нижняя мертвая точка — крайнее нижнее положение поршня, где меняется направление его движения.
Ход поршня — расстояние между крайними положениями поршня. Равно удвоенному радиусу кривошипа.
Блок цилиндров, поршень с шатуном и коленвалВидео:
- Старинная русская прялка с кривошипно-шатунным механизмом
- Паровая машина. Джеймс Уатт
- Принцип работы противовесов
Литература:
- КИНЕМАТИКА И ДИНАМИКА КРИВОШИПНОШАТУННОГО МЕХАНИЗМА ПОРШНЕВЫХ ДВИГАТЕЛЕЙ
Обычный маятник, если перевернуть его кверху ногами, неустойчив. Для него крайне трудно найти верхнюю точку равновесия. Но если совершать быстрые вертикальные возвратно-поступательные колебания, то положение такого маятника становится устойчивым.
Для него крайне трудно найти верхнюю точку равновесия. Но если совершать быстрые вертикальные возвратно-поступательные колебания, то положение такого маятника становится устойчивым.
Советский академик и нобелевский лауреат по физике Петр Леонидович Капица (1894 — 1984) использовал модель маятника с вибрирующим подвесом для построения новой теории, которая описывала эффекты стабилизации тел или частиц. Работа Капицы по стабилизации маятника была опубликована в 1951 году, а сама модель получила название «маятник Капицы». Более того, было открыто новое направление в физике — вибрационная механика. Данная модель позволила наглядно показать возможности высокочастотной электромагнитной стабилизации пучка заряженных частиц в ускорителях.
Владимир Игоревич АрнольдДругой советский математик и академик Владимир Игоревич Арнольд (1937-2010), который был заместителем Капицы, вспоминал его слова:
«Он (Капица — примечание) сказал: «Вот смотрите — когда придумывается какая-то физическая теория, то прежде всего надо сделать маленький какой-нибудь прибор, на котором его наглядно можно было-бы продемонстрировать кому угодно. Например, Будкер и Векслер хотят делать ускорители на очень сложной системе. Но я посмотрел, что уравнения, которые говорят об устойчивости этого пучка, означают, что если маятник перевернут кверху ногами, он обычно неустойчив, падает. Но если точка подвеса совершает быстрые вертикальные колебания, то он становится устойчивым. В то время как ускоритель стоит много миллионов, а этот маятник можно очень легко сделать. Я его сделал на базе швейной электрической машинки, он вот здесь стоит». Он нас отвел в соседнюю комнату и показал этот стоящий вертикально маятник на базе швейной машинки».
Например, Будкер и Векслер хотят делать ускорители на очень сложной системе. Но я посмотрел, что уравнения, которые говорят об устойчивости этого пучка, означают, что если маятник перевернут кверху ногами, он обычно неустойчив, падает. Но если точка подвеса совершает быстрые вертикальные колебания, то он становится устойчивым. В то время как ускоритель стоит много миллионов, а этот маятник можно очень легко сделать. Я его сделал на базе швейной электрической машинки, он вот здесь стоит». Он нас отвел в соседнюю комнату и показал этот стоящий вертикально маятник на базе швейной машинки».
У математика Арнольда не было своей швейной машинки, и он огорчился. Но у него была электробритва «Нева», из которой и был собран перевернутый маятник. К сожалению, в первой конструкции маятник падал. Тогда Арнольд вывел формулу и увидел, что длина маятника не должна быть больше 12 сантиметров. Известный математик укоротил подвес до 11 сантиметров и все получилось.
Давайте посмотрим, какие силы действуют на «маятник Капицы». После прохождения верхней мертвой точки подвес маятника начинает тянуть грузик вниз. После прохождения нижней мертвой точки подвес толкает грузик вверх. Так как углы вежду векторами сил в верхней и нижней точке разные, то сумма их векторов дает силу, направленную к оси вертикальных колебаний маятника. Если эта сила больше силы тяжести, то верхнее положение маятника становится устойчивым.
А эта формула описывает взаимосвязь частоты вибраций подвеса, амплитуды колебаний и длины жесткого подвеса.
Видео:
- GetAClass. Маятник Капицы
- Маятник Капицы: диалог академика Арнольда и Капицы, вывод формулы
свидетельство о государственной регистрации программы для ЭВМ — Научно-исследовательский портал Уральского федерального университета
TY — PAT
T1 — Кинематическая модель управления плоским роботом-манипулятором (кривошипно-шатунный механизм)
T2 — свидетельство о государственной регистрации программы для ЭВМ
AU — Берестова, Светлана Александровна
AU — Мамылин, Дмитрий Андреевич
AU — Воронцов, Максим Александрович
PY — 2020/1/17
Y1 — 2020/1/17
N2 — Программа реализует алгоритм плавного движения плоского робота-манипулятора, моделируемого кривошипно-шатунным механизмом. Рабочий инструмент при этом движется по наперед-заданной в полярных координатах гладкой траектории. Позволяет определять и визуализировать положение всех звеньев механизма в любой момент времени и траекторию рабочего инструмента. Выполняет анимацию движения робота-манипулятора с возможностью изменения его геометрических параметров при произвольно заданном законе движения рабочего инструмента. Программа дает возможность визуализировать законы изменения кинематических характеристик, таких как скорость и ускорение рабочего инструмента, а также шарнира, соединяющего кривошип и шатун; угловую скорость и угловое ускорение кривошипа и шатуна. Программа может быть использована в робототехнике при решении задач управления, для определения кинематических и инерционных характеристик звеньев робота-манипулятора, а также в учебном процессе для имитационного моделирования движения плоского робота-манипулятора, определения кинематических характеристик звеньев кривошипно-шатунного механизма. Предназначена для студентов бакалавриата, магистратуры, аспирантов, преподавателей, а также специалистов в области робототехники. Тип ЭВМ: IBM РC — совмест. ПК. ОС: Windows.
AB — Программа реализует алгоритм плавного движения плоского робота-манипулятора, моделируемого кривошипно-шатунным механизмом. Рабочий инструмент при этом движется по наперед-заданной в полярных координатах гладкой траектории. Позволяет определять и визуализировать положение всех звеньев механизма в любой момент времени и траекторию рабочего инструмента. Выполняет анимацию движения робота-манипулятора с возможностью изменения его геометрических параметров при произвольно заданном законе движения рабочего инструмента. Программа дает возможность визуализировать законы изменения кинематических характеристик, таких как скорость и ускорение рабочего инструмента, а также шарнира, соединяющего кривошип и шатун; угловую скорость и угловое ускорение кривошипа и шатуна. Программа может быть использована в робототехнике при решении задач управления, для определения кинематических и инерционных характеристик звеньев робота-манипулятора, а также в учебном процессе для имитационного моделирования движения плоского робота-манипулятора, определения кинематических характеристик звеньев кривошипно-шатунного механизма. Предназначена для студентов бакалавриата, магистратуры, аспирантов, преподавателей, а также специалистов в области робототехники. Тип ЭВМ: IBM РC — совмест. ПК. ОС: Windows.
UR — https://www.elibrary.ru/item.asp?id=42497422
M3 — Патент
M1 — 2020610626
Y2 — 2019/12/30
PB — Федеральный институт промышленной собственности
ER —
Кривошипно-шатунный механизм двигателя трактора
Категория:
Тракторы
Публикация:
Кривошипно-шатунный механизм двигателя трактора
Читать далее:
Кривошипно-шатунный механизм двигателя трактора
Кривошипно-шатунный механизм состоит из следующих основных частей: цилиндра (рис. 1), поршня с кольцами, шатуна с подшипником, поршневого пальца, коленчатого вала с противовесами, вращающегося в подшипниках, и маховика.
Детали кривошипно-шатунного механизма воспринимают большое давление (до 6…8 МПа) газов, возникающих при сгорании топлива в цилиндрах, а некоторые из них, кроме того, работают в условиях высоких температур (350° и выше) и при большой частоте вращения коленчатого вала. Чтобы детали могли удовлетворительно работать длительное время (не менее 8…9 тыс. часов) в таких тяжелых условиях, обеспечивая работоспособность двигателя, их изготавливают с большой точностью из высококачественных прочных металлов и их сплавов, а детали из черных металлов (сталь, чугун), кроме того, подвергают термической обработке (цементации, закалке).
Рекламные предложения на основе ваших интересов:
Рис. 1. Кривошипно-шатунный механизм:
1 – коренной подшипник; 2 — шатунный подшипник; 3 — шатун; 4 — поршневой палец; 5 — поршневые кольца; 6 — поршень; 7 — цилиндр; 8 — маховик; 9 — противовес; 10 — коленчатый вал.
Отдельные детали кривошипно-шатунного механизма имеют следующее устройство.
Цилиндр (рис. 2) — основная часть двигателя, внутри которой сгорает топливо. Цилиндр изготавливают в виде отдельной отливки, укрепляемой на чугунной коробке — картере, или в виде сменной гильзы, вставляемой в блок цилиндров. Материалом для изготовления цилиндров и гильз служит чугун. Внутреннюю поверхность цилиндров и гильз, называемую зеркалом цилиндра, делают строго цилиндрической формы и подвергают шлифовке и полировке. Число цилиндров или гильз у одного двигателя может быть различно: один, два, три, четыре, шесть и больше.
Блок цилиндров может быть изготовлен так, что цилиндры будут расположены в один или в два ряда под углом в 90°.
Блок цилиндров и картер снизу закрыты поддоном и уплотнены прокладками. Цилиндры сверху закрыты головкой (в зависимости от конструкции двигателя), уплотняемой металло-асбестовой прокладкой.
Поршень, устанавливаемый внутри цилиндра, сжимает свежий заряд воздуха и воспринимает давление расширяющихся газов во время горения топлива и передает это давление через палец и шатун на коленчатый вал, заставляя его вращаться. Поршень отливается из алюминиевого сплава. На боковых стенках поршня делают два прилива — бобышки с отверстиями, в которые вставляется поршневой палец, соединяющий поршень с шатуном. В днище поршня сделана специальная камера, способствующая лучшему перемешиванию топлива с воздухом.
Рис. 2. Детали двигателя:
1 — блок-картеры; 2, 4 — головки цилиндров; 3, 8— прокладки; 5 — цилиндр; 6 — картер; 7 — гильза; 9 — поршень; 10 — поддон; 12 — вкладыши; 13 — крышка шатуна; 14 — стопорное кольцо; 15 — поршневой палец; 16 — шатун; 17 — втулка; 18 — шплинт; 19 — болт; 20 — коренной подшипник.
Поршень во время работы сильно нагревается (до 350 °С) и при этом расширяется. Во избежание заклинивания поршня в цилиндре его делают несколько меньшего диаметра, чем цилиндр, создавая тем самым между ними зазор 0,25…0,40 мм.
Поршневые кольца. Поскольку между поршнем и цилиндром имеется зазор, то через него могут проходить из камеры сжатия в картер газы. Из картера в камеру сжатия попадает и там сгорает смазочное масло, при этом увеличивается его расход.
Для устранения подобных явлений на поршень в специальные канавки надевают пружинные чугунные кольца. Диаметр колец делают немного больше диаметра цилиндра, в котором они будут работать. Чтобы такое кольцо можно было вставить в цилиндр, в нем сделан вырез (или, как его еще называют, замок), позволяющий сжать кольцо перед постановкой в цилиндр. Такое кольцо, будучи вставлено в цилиндр, стремится занять первоначальное положение и поэтому плотно прилегает к стенкам цилиндра, закрывая при этом своим телом зазор между поршнем и цилиндром.
Во время работы двигателя кольца, кроме уплотнения, обеспечивают распределение смазки по цилиндру, предотвращают попадание масла в камеру сгорания, уменьшая тем самым расход его, а также отводят теплоту от сильно нагретого поршня к стенкам цилиндра.
По назначению кольца бывают двух типов: компрессионные — уплотняющие (их обычно ставят по три-четыре) и маслосъемные (одно-два).
Компрессионные кольца воспринимают силы давления газов, причем наибольшую нагрузку до 75 % давления несет первое кольцо. Чтобы предохранить поршень от повышенного износа, у некоторых двигателей в первую канавку поршня устанавливают стальную вставку, а для уменьшения износа кольца его цилиндрическую поверхность покрывают пористым хромом. Остальные кольца, воспринимающие меньшую нагрузку — 20 и 5 % сил давления, хромом не покрывают.
Маслосъемные кольца чаще всего делают коробчатого сечения с прорезями. Благодаря этому усилие прижатия кольца к стенке цилиндра передается через два узких пояска, что увеличивает удельное давление кольца. Кроме того, узкие пояски кольца лучше снимают излишнее масло со стенок цилиндра или гильзы при движении поршня вниз.
На дне канавки маслосъемного кольца сделаны отверстия в поршне, через которые отводится масло, собранное со стенок цилиндра.
У некоторых двигателей, для того чтобы увеличить упругость маслосъемных колец, в зазор между кольцом и канавкой устанавливают стальной расширитель.
Шатун соединяет поршень с коленчатым валом. Его штампуют из стали. Он состоит из верхней и нижней головок и стержня. Верхняя, неразъемная, головка служит для соединения с поршнем, в нее вставляется поршневой палец. Для уменьшения трения между пальцем и шатуном в верхнюю головку запрессовывают бронзовую втулку. Нижняя, разъемная, головка имеет крышку и охватывает шейку коленчатого вала. Чтобы уменьшить трение шатуна о шейку вала, в нижнюю головку и крышку устанавливают вкладыши — стальные пластины, у которых поверхность, прилегающая к шейке вала, покрыта тонким слоем свинцовистой бронзы или специальным алюминиевым сплавом.
Нижнюю головку шатуна и ее крышку соединяют шатунными болтами, гайки которых после затяжки шплинтуют.
Поршневой палец, соединяющий шатун с поршнем, изготовляют из стали, а наружную поверхность подвергают термической (цементации и закалке) и механической (шлифовке) обработке.
Палец во время работы двигателя может перемещаться в верхней головке шатуна и бобышках поршня в небольших пределах, поэтому его называют плавающим. Для того чтобы палец во время работы не вышел из поршня и не поцарапал зеркало цилиндра, ограничивают перемещение пальца в осевом направлении, устанавливая в бобышках (приливах) поршня стопорные пружинные кольца, которые, не препятствуя пальцу поворачиваться в бобышках и головке шатуна, не позволяют ему перемещаться за пределы поршня.
Коленчатый вал воспринимает через шатуны силы расширяющихся газов, действующих на поршни, и превращает эти силы во вращательное движение, которое затем передается трансмиссии трактора. От коленчатого вала также приводятся в движение и другие устройства и механизмы двигателя (газораспределительный, топливный и масляный насосы и др.). Коленчатый вал штампуют из стали или отливают из специального чугуна. Коленчатый вал состоит из следующих частей: коренных или опорных шеек, на которых он вращается в коренных подшипниках, шатунных шеек, которые охватывают нижние головки шатунов, щек, соединяющих шейки между собой, и фланца, предназначенного для крепления маховика.
Чтобы продлить срок службы коленчатого вала, поверхности шеек подвергают термической обработке — закалке.
Маховик представляет собой массивный диск, отлитый из чугуна, он укрепляется на фланце заднего конца коленчатого вала.
Маховик во время работы двигателя накапливает кинетическую энергию, уменьшает неравномерность частоты вращения коленчатого вала, выводит поршни из мертвых точек и облегчает работу двигателя при разгоне машинно-тракторного агрегата и преодолении кратковременных перегрузок.
На маховике укрепляется зубчатый венец, через который специальными устройствами вращают коленчатый вал при пуске двигателя.
—
Основными деталями кривошипно-шатуиного механизма являются: цилиндры, поршни в комплекте с кольцами и поршневыми пальцами, шатуны в комплекте со втулками в верхней головке и подшипниками в нижней головке, коленчатый вал с коренными подшипниками и маховик.
Цилиндры выполнены в виде отдельных гильз, вставленных в отверстия блока цилиндров. Такое устройство упрощает изготовление блока и дает возможность заменять изношенные или поврежденные гильзы новыми. Они отливаются из легированного чугуна. Внутренняя поверхность гильзы закалена. На наружной поверхности имеются два посадочных и один опорный пояски. Сверху гильза прижимается головкой. Гильзы омываются охлаждающей жидкостью, циркулирующей в рубашке блока. Для предотвращения попадания ее в масляный поддон гильзы имеют по две кольцевые канавки, в которых установлены уплотнительные резиновые кольца.
Поршень отливается из высококремнистого алюминиевого сплава. В днище поршня имеется фасонная выемка, являющаяся камерой сгорания. В головке поршня выполнены кольцевые канавки для компрессионных колец. Вместе с кольцами головка является уплотняющей частью поршня. В бобышках поршня сделаны отверстия для поршневого пальца и канавки для установки стопорных колец. Направляющая часть поршня имеет кольцевые канавки для маслосъем-ных колец.
На каждом поршне расположены три компрессионных и два масло-съемных кольца. Компрессионные кольца имеют трапецеидальное сечение. Верхнее кольцо предотвращает прорыв воздуха и газов из надпоршневого пространства в картер. Оно наиболее нагружено давлением газов, сильно нагревается и работает при недостаточной смазке. Для уменьшения истирания на наружную поверхность кольца наносят пористый слой износостойкого металла — хрома. Масло, находящееся в порах, уменьшает трение и износ кольца и гильзы. Когда поршень совершает движение, компрессионные кольца прижимаются то к нижней, то к верхней кромке его канавок и создают необходимое уплотнение, препятствующее прорыву газов в картер.
Маслосъемные кольца касаются цилиндра узкими кромками и хорошо снимают масло с его зеркала. Масло по сверлениям в поршне стекает в поддон двигателя. Чтобы предотвратить прорыв газов в картер, замки соседних колец смещают относительно друг друга по окружности.
Для обеспечения точной посадки поршни и гильзы имеют шесть размерных групп, обозначаемых клеймами на днищах поршней и на верхних торцах гильз. При сборке поршень и гильза должны подбираться из одних размерных групп.
Поршневой палец соединяет шарнирно поршень с шатуном. Палец пустотелый; в отверстие шатуна он вставляется с зазором, а в бобышки поршня без зазора. Во время работы двигателя бобышка нагревается и появляется зазор между ней и пальцем. Палец свободно поворачивается в шатуне и бобышке. Осевое перемещение пальца ограничивается стопорными кольцами.
Шатун представляет собой стальную фасонную поковку и состоит из стержня и двух головок (верхней и нижней). Верхняя головка через поршневой палец соединяется с поршнем, нижняя — с коленчатым валом. Стержень двутаврового сечения, что придает ему при небольшой массе достаточную прочность. В верхнюю головку запрессована бронзовая втулка. По каналу в стержне и радиальным отверстиям во втулке подводится смазка к поршневому пальцу. Нижняя головка имеет разъем под углом 55° к оси стержня. Это позволяет устанавливать и снимать комплект поршня с шатуном через цилиндр.
Съемная часть шатуна называется крышкой. Стык шатуна с крышкой имеет форму гребенки с треугольными зубьями. Это надежно предохраняет крышку от радиального сдвига относительно шатуна. Осевая фиксация крышки на шатуне осуществляется штифтом, запрессованным в шатун и входящим в паз крышки. У одного стыка со стороны длинного болта имеются метки спаренности (двузначное число), одинаковые для обеих частей, и риски на обеих частях шатуна. Крышки шатунов не взаимозаменяемые.
В нижней головке шатуна и его крышке расположен подшипник, охватывающий шатунную шейку коленчатого вала. Он состоит из тонкостенных вкладышей 6, изготовленных из сталеалюминиевой полосы. Вкладыши удерживаются в теле шатуна и в крышке вследствие плотной посадки и наличия ушков, которые входят в выточки нижней головки и ее крышки. Болты крепления крышки предохраняются от самоотворачивания замковыми шайбами с усами, отогнутыми на грани болтов и крышки. Оба вкладыша нижней головки шатуна взаимозаменяемы.
Коленчатый вал состоит из четырех шатунных и пяти коренных шеек, щек, передней части и хвостовика, уравновешивающих противовесов. В шатунных шейках есть закрытые заглушками внутренние полости, в которых масло подвергается дополнительной Центробежной очистке. Эти полости сообщаются наклонными каналами с радиальными каналами в коренных шейках.
Для уменьшения действия центробежных сил на щеках коленчатого вала устанавливаются противовесы. Кроме того, имеются две выносные массы, одна из которых выполнена в виде прилива на маховике, другая представляет собой противовес, напрессованный на передний конец коленчатого вала. Вал балансируется в сборе с противовесами. В осевом направлении он фиксируется четырьмя бронзовыми полукольцами, установленными в выточках задней коренной опоры. Для предохранения от проворачивания нижние полукольца своими пазами входят в штифты, запрессованные в крышку коренного подшипника.
Носок и хвостовик коленчатого вала уплотняются самоподжимными сальниками.
Вкладыши коренных подшипников состоят из сменных тонкостенных элементов, изготовленных из сталеалюминиевой полосы. Верхний и нижний вкладыши коренных подшипников не взаимозаменяемые. В верхнем вкладыше имеется отверстие; для подвода масла и канавки для его распределения.
Для ремонта коленчатого вала предусмотрено шесть ремонтных размеров шеек и вкладышей. Клеймо наносится на тыльную сторону вкладыша недалеко от стыка.
Маховик крепится болтами к заднему торцу вала и точно фиксируется относительно шеек коленчатого вала двумя штифтами. Зубчатый венец служит для пуска двигателя стартером. Двенадцать радиальных отверстий предназначены для проворачивания коленчатого вала при регулировках двигателя.
Рекламные предложения:
Читать далее: Уравновешивающий механизм
Категория: — Тракторы
Главная → Справочник → Статьи → Форум
Конструкция кривошипно-шатунного механизма | Строительство автомобилей
Кривошипно-шатунный механизм предназначен для преобразования возвратно-поступательного движения поршней во вращение коленчатого вала .
Детали кривошипно-шатунного механизма можно разделить на две группы: стационарные, и подвижные.
Подвижные элементы кривошипно-шатунного механизма: поршни , поршневые кольца, поршневые пальцы, шатуны, коленчатый вал, маховик.
Стационарные компоненты кривошипно-шатунного механизма : блок цилиндров двигателя , блок головки двигателя, поддон, цилиндры .
Стационарные детали двигателяПоршень — компонент двигателя внутреннего сгорания . Назначение поршня — передача усилия от расширяющегося газа в цилиндре на коленчатый вал через шатун.
Поршневые кольца — это разрезное кольцо, которое входит в канавку на внешнем диаметре поршня в двигателе внутреннего сгорания .
Шатун — это элемент, который соединяет поршень с коленчатым валом в поршневом двигателе.
Коленчатый вал — — это механическая часть, выполняющая преобразование возвратно-поступательного движения поршня и шатуна во вращательное движение. Когда дефект коленчатого вала невозможно избежать дорогостоящего ремонта, поэтому здесь вы можете увидеть стоимость ремонта коленчатого вала .
Маховик — это механическое устройство, предназначенное для эффективного хранения энергии вращения коленчатого вала .
Блок цилиндров двигателя — это конструкция, которая содержит цилиндров и другие части двигателя внутреннего сгорания.
Головка блока цилиндров двигателя — находится над цилиндрами в верхней части блока цилиндров в двигателе.
Цилиндр — центральная рабочая часть двигателя , пространство, в котором перемещается поршень .
Кривошипно-ползунковый механизм: новое в системе Mathematica 9
X
\! \ (\ * GraphicsBox [{GraphicsGroupBox [GeometricTransformationBox [ {Оттенок [0.05, 0.3, 0.9], EdgeForm [{GrayLevel [0], AbsoluteThickness [ 0.5]}], RectangleBox [{0.7140365793403993, -0.06}, \ {0.9940365793403994, 0,06}], {GrayLevel [0,7], EdgeForm [Нет], RectangleBox [{0.20999999999999996`, -0.11000000000000001`}, \ {1.19, -0.06}], {GrayLevel [0], AbsoluteThickness [0,5], LineBox [{{0.20999999999999996`, -0.06}, {1.19, -0.06}}], {GrayLevel [0,7], EdgeForm [Нет], RectangleBox [{0.20999999999999996`, 0.11000000000000001`}, \ {1.19, 0.06}], {GrayLevel [0], AbsoluteThickness [0.5], LineBox [{{0.20999999999999996`, 0,06}, {1.19, 0,06}}]}}}}}, {{{1, 0}, {0, 1}}, {0., 0.}}]], GraphicsGroupBox [GeometricTransformationBox [ {Оттенок [0,6, 0,2, 0,7], EdgeForm [{GrayLevel [0], AbsoluteThickness [0,5]}], PolygonBox [CompressedData [» 1: eJxTTMoPSmViYGBQAmIQDQPVIuvch2Yt2c / 88lzium / 1 + z1SfHYoiy3ZP29p L0dJZP9 + n6smcqdeL9pvbMJRO / ngtP3abanzvdkX7r / D8t + / 99scOA0Th6mD 6YOZAzMXZg / MXpg70OTt0fTbo5lvj2a / PZr77NHcb4 / mP3s0 / 9sbg8Flexj / et6uN7ybL9vD1CcsKL / 8T / cKzF32ZduYs33mX4G5y75R2ZhjDtNVmLvsfzyW Xy4TctUe7t6zP8vWTLgKc5f9nv02q75vvQpzl / 2hrxox / Yeuwt2FJr8fTf9 + NPP3o9m / H819 + 9Hcvx / Nf / vR / L8fAN4bAVc = «]], {GrayLevel [0], AbsolutePointSize [5], PointBox [{0, 0}], PointBox [{0.3, 0}]}}, {{{ 0,6427876096865393, -0,766044443118978}, {0,766044443118978, 0.6427876096865393}}, {0, 0}}]], GraphicsGroupBox [GeometricTransformationBox [ {GrayLevel [0,85], EdgeForm [{GrayLevel [0], AbsoluteThickness [0,5]}], PolygonBox [CompressedData [» 1: eJxTTMoPSmViYGAQBmIQPWsmCKzcD6F37o9ImOJWHz5v / + SUvK0MlsX2ukxV FxzZ5u6fZNEZqavYYr / 10OfKaWdn7X / PMvFPBGufffqR / zON90 / fz9P8L0Go drJ9CF / s / PLPk / e3PK3IEo6Zbt / 0cXqzr2D // j1H9 ++ 52DDLvu30scjPzq37 S / nmL7G5NMc + bYnwYqFZpftTjl0pvWE7z361wP / InI8Je3bItb4O3DHPPhQi b58Kla + H6LevgOrvgJhvvwtqfhjEfvsmqP0pEPfZ80PdtwXifvvvUPdrQfxn vwLqP6j / 7Vuh / oeGjz0sfABj1Jnp «]], {GrayLevel [0.7], EdgeForm [Нет], RectangleBox [{- 0.1, -0.15000000000000002`}, {0.1, -0.1}], {GrayLevel [0], AbsoluteThickness [0,5], LineBox [{{- 0,1, -0,1}, {0,1, -0,1}}], {GrayLevel [0], AbsolutePointSize [5], PointBox [{0, 0}]}}}}, {{{1, 0}, { 0, 1}}, {0, 0}}]], GraphicsGroupBox [GeometricTransformationBox [ {Оттенок [0,6, 0,2, 0,9], EdgeForm [{GrayLevel [0], AbsoluteThickness [0,5]}], PolygonBox [{{0,192836282
178`, 0,14981333293569338`}, { 0,192836282178`, 0,3098133329356934}, { 0.89283628217, 0,2778133329356934}, {0,89283628217, 0,1818133329356934}}], {RGBColor [0,8600000000000001, 0,8960000000000001, 0,95], DiskBox [{0,192836282178`, 0,2298133329356934}, 0,08], DiskBox [{0,89283628217, 0,2298133329356934}, 0,048]}, {GrayLevel [0,5], DiskBox [{0,192836282178`, 0,2298133329356934}, 0,032], DiskBox [{0.89283628217, 0.2298133329356934}, 0,0192]}}, {{{0,94457185204, 0,32830476133670483 ‘}, {-0.32830476133670483`, 0,94457185204}}, {-0,06476025340225089, 0,07604719725552594}}]], {GrayLevel [0], AbsoluteThickness [0,5], Стрелки [Средний], ArrowBox [{{- 0,25, 0}, {0,5, 0}}], ArrowBox [{{0, -0.05}, {0, 0.6}}], { GraphicsGroupBox [GeometricTransformationBox [ {GrayLevel [0], AbsoluteThickness [0,5], LineBox [{{0, 0.07}, {0, 0.17}}], {Стрелки [{- маленькие, маленькие}], ArrowBox [{{0, 0.12000000000000001`}, {0.3, 0.12000000000000001`}}], LineBox [{{0.3, 0,07}, {0,3, 0,17}}], InsetBox [ StyleBox [«\ <\" \\! \\ (\\ * SubscriptBox [\\ (l \\), \\ (1 \\)] \\) \ "\>«, StripOnInput-> False, FontSize-> 12], {0,15, 0.12000000000000001`}, Фон-> GrayLevel [1]]}}, {{{ 0,6427876096865393, -0,766044443118978}, {0,766044443118978, 0.6427876096865393}}, {0, 0}}]], GraphicsGroupBox [GeometricTransformationBox [ {GrayLevel [0], AbsoluteThickness [0,5], LineBox [{{0.192836282178`, 0.4298133329356934}, { 0.192836282178`, 0.5298133329356934}}], {Стрелки [{- маленькие, маленькие}], ArrowBox [{{0.192836282178`, 0.4798133329356934}, { 0,89283628217, 0,4798133329356934}}], LineBox [{{0.89283628217, 0.4298133329356934}, { 0,89283628217, 0,5298133329356934}}], InsetBox [ StyleBox [«\ <\" \\! \\ (\\ * SubscriptBox [\\ (l \\), \\ (2 \\)] \\) \ "\>», StripOnInput-> False, FontSize-> 12], {0.54283628218, 0.4798133329356934}, Фон-> GrayLevel [1]]}}, {{{0,94457185204, 0.32830476133670483`}, {-0.32830476133670483`, 0,94457185204}}, {-0,06476025340225089, 0,07604719725552594}}]], GraphicsGroupBox [GeometricTransformationBox [ {GrayLevel [0], AbsoluteThickness [0,5], LineBox [{{0, -0.35}, {0, -0.24999999999999997`}}], {Стрелки [{- маленькие, маленькие}], ArrowBox [{{0, -0.3}, {0.8540365793403993, -0.3}}], LineBox [{{0.8540365793403993, -0.35}, { 0.8540365793403993, -0.24999999999999997`}}], InsetBox [ StyleBox [«\ <\" \\! \\ (\\ * SubscriptBox [\\ (z \\), \\ (3 \\)] \\) \ "\>», StripOnInput-> False, FontSize-> 12], {0.42701828967019967`, -0,3}, Фон-> GrayLevel [1]]}}, {{{1, 0}, {0, 1}}, {0., 0.}}]], {GrayLevel [0], AbsoluteThickness [0,5], GeometricTransformationBox [ LineBox [{{0, 0}, {-0.25, 0}}], {{{ 0,6427876096865393, -0,766044443118978}, {0,766044443118978, 0,6427876096865393}}, {0, 0}}], CircleBox [{0, 0}, 0,2, NCache [{Pi, Rational [23, 18] Pi}, {3.141592653589793, 4.014257279586958}]], GeometricTransformationBox [ LineBox [{ Смещение [{- 3, 6}, {-0.2, 0}], смещение [{0, 0}, {-0.2, 0}], Смещение [{3, 6}, {-0.2, 0}]}], {{{ 0,6427876096865393, -0,766044443118978}, {0,766044443118978, 0,6427876096865393}}, {0, 0}}], {GrayLevel [0], InsetBox [ StyleBox [«\ <\" \\! \\ (\\ * SubscriptBox [\\ (\ [Alpha] \\), \\ (1 \\)] \\) \ "\>», StripOnInput-> False, FontSize-> 12], {-0.2, -0.08}, {-1, 0}, Фон-> GrayLevel [1]], LineBox [{{0.192836282178`, 0.2298133329356934}, { 0,39283628218, 0,2298133329356934}}], GeometricTransformationBox [ LineBox [{{0.192836282178`, 0,2298133329356934}, { 0,39283628218, 0,2298133329356934}}], {{{ 0,94457185204, 0,32830476133670483`}, {-0,32830476133670483`, 0,94457185204}}, {-0,06476025340225089, 0,07604719725552594}}], CircleBox [{0,192836282178`, 0,2298133329356934}, 0,15, { 0, 5.948677009576}], GeometricTransformationBox [ LineBox [{ Смещение [{- 3, -6}, {0,34283628218, 0,2298133329356934}], Смещение [{0, 0}, {0.34283628218, 0,2298133329356934}], Смещение [{3, -6}, {0,34283628218, 0,2298133329356934}]}], {{{0,94457185204, 0,3283047613367053}, {-0,3283047613367053, 0,94457185204
}}, {-0,06476025340225089, 0,07604719725552606}}]}, {GrayLevel [0], InsetBox [ StyleBox [«\ <\" \\! \\ (\\ * SubscriptBox [\\ (\ [Alpha] \\), \\ (2 \\)] \\) \ "\>», StripOnInput-> False, FontSize-> 12], {0.192836282
178`, 0.3798133329356934}, {-1, 0}, Фон-> GrayLevel [1]]}}}}, {Оттенок [0, 1, 0.8], AbsoluteThickness [2], Opacity [1], Arrowheads [Medium], ArrowBox [{{1.2040365793403993`, 0}, {1.0040365793403994`, 0}}], {GrayLevel [0], InsetBox [ StyleBox [«\ <\" F (t) \ "\>«, StripOnInput-> False, FontSize-> 12, FontSlant-> Italic], {1.2240365793403993`, 0}, {-1, 0}]}}}, ImageSize -> {470.6796875, Автоматически}, PlotRange -> {{- 0.5, 1.5}, {-0.47, 0.6}}] \)Кривошипно-ползунковый механизм
Кривошипно-ползунковый механизмНАЖМИТЕ ЗДЕСЬ ДЛЯ УКАЗАТЕЛЬНОЙ СТРАНИЦЫ
КОЛЕСА И СЛАЙДЕР
В.Райан 2002 — 2020
| ФАЙЛ PDF — НАЖМИТЕ ЗДЕСЬ ДЛЯ ПЕЧАТИ РАБОЧЕГО ЛИСТА | |
Этот механизм состоит из трех важных частей: Кривошип, который является вращающийся диск, ползунок который скользит внутри трубки и шатуна который соединяет части вместе. | |
При движении ползуна вправо шатун толкает колесо по кругу на первые 180 градусов вращения колеса. Когда ползунок начинает двигаться обратно в трубку, шатун тянет колесо вращается, чтобы завершить вращение. | |
| Альтернативная компоновка кривошипа и ползуна | |
Найдите еще два примера кривошипа и ползуна механизмы, нарисуйте схемы и используйте примечания, чтобы объяснить, как они работают. | |
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ УКАЗАТЬ МЕХАНИЗМЫ СТР. | |
Динамический анализ кривошипно-шатунного механизма с неисправностью зазора
2.1. Динамическая модель, основанная на состоянии непрерывного контакта
Предположим, что имеется чрезмерный зазор в поворотном шарнире B между коленчатым валом и шатуном в кривошипно-скользящем механизме, показанном на рис. 1. Учитывая, что зазор в поворотном шарнире B очень мал, время столкновения и контакта подвижные боковые элементы очень короткие, поэтому предполагается, что подвижные соединения всегда находятся в контакте, а столкновение и разделение завершаются мгновенно.За счет упрощения и игнорирования упругой деформации и демпфирования контактной поверхности подвижных соединений зазор эквивалентен виртуальному жесткому стержню того же размера. Когда в механизме происходит резкое изменение определенного азимута, считается, что подвижные соединения находятся в разъединенном состоянии. После эквивалента модели зазора механизм превращается в систему с несколькими стержнями и несколькими степенями свободы, и уравнение Лагранжа может использоваться для установления динамического уравнения системы.Второй тип уравнения Лагранжа выражается следующим образом:
(1)
ddt∂E∂q˙i-∂E∂qi + ∂U∂qi = Fi,, где E и U представляют собой сумму кинетической энергии и потенциальной энергии кривошипно-ползункового механизма соответственно. Fi — обобщенная сила.
Поскольку система, показанная на рис. 1, имеет только одну степень свободы, следует ввести обобщенную координату θ. Уравнение (1) превратится в формулу. (2):
(2)
ddt∂E∂θ˙i-∂E∂θ + ∂U∂θ = 0,где θ — введенная обобщенная координата.Нетрудно найти, что выражение суммы кинетической энергии коленчатого вала, шатуна и ползуна выглядит следующим образом:
(3)
E = 12m2x˙32 + 12m3x˙32 + 1213m1l12θ˙12 + 1213m2l22θ˙22,где m1, m2 и m3 — массы коленчатого вала, шатуна и ползуна соответственно. l1, l2 — длины коленчатого вала и шатуна соответственно. θ1, θ2 и θ представляют угол между коленчатым валом, звеном, виртуальным стержнем и осью x соответственно.
Аналогичным образом сумма потенциальной энергии коленчатого вала, шатуна и ползуна может быть получена следующим образом:
(4)
U = 12m1gl1sinθ1 + 12m2gl2sinθ2.Подставляя уравнения. (3) и (4) в уравнение. (2) дает выражение:
(5)
ddt∂E∂θ˙ = m2 + m3x¨3∂x3∂θ + x˙3∂x˙3∂θ + 13m2l22θ¨2∂θ2∂θ + θ˙2∂θ˙2∂θ, ∂E∂θ = m3 + m2x˙3∂x˙3∂θ + 13m2l22θ˙2∂θ˙2∂θ, ∂U∂θ = 12m2gl2cosθ2∂θ2∂θ.Рис. 1. Принципиальная схема кривошипно-шатунного механизма при разрыве зазора
Подставляя уравнения.(3) и (4) в уравнение. (2) дает выражение:
(6)
(m2 + m3) x¨3∂x3∂θ + 13m2l22θ¨2∂θ2∂θ + 12m2gl2cosθ2∂θ2∂θ = 0,где:
x¨3 = -l1θ¨1sinθ1 + θ˙12cosθ1 + rθ¨sinθ + θ˙2cosθ + l2θ¨2sinθ2 + θ˙22cosθ2, ∂x3∂θ = -rsinθ-l2sinθ2∂θ2∂θ, ∂θ2∂θ = rcosθl2cosθ2, sinθ2 = l1sinθ1 + rsinθl2, cosθ2 = 1-l1sinθ1 + rsinθl22, θ¨2 = sinθ2l22cos3θ2 (l1θ˙1cosθ1 + rθ˙cosθ) 2 + 1l2cosθ2l1θ¨1cosθ1-θ˙12cosθ1 + r .θ12sinθ1 + r.
2.2. Трехступенчатая динамическая модель
В этой статье в программном обеспечении ADAMS была принята модель динамики на основе трех состояний.В системе ADAMS зазор между трением и ударом характеризуется созданием модели контактной силы. Модель контактной силы записывается следующим образом:
(7)
УДАР x, x, ˙x1, k, e, cmax, d,, где x используется для вычисления расстояния между точками двух геометрических объектов, которые будут соприкасаться. x˙ ̇ — это производная по времени от x, которая представляет собой скорость столкновения или отрыва. x1 — свободная длина x, то есть, когда x В этой статье УДАР можно определить следующим выражением: (8)
(9)
ШАГδ, 0,0, δmax, Cmax = 0, δ≤0, Cmaxδδmax23-2δδmax, 0 <δ <δmax, Cmax, δ≥δmax,где, когда δmax положительно, определение Cmax является максимальным, а разумный параметр составляет 0,0l мм.
Рис. 2. Функция ШАГ
Динамический анализ кривошипно-ползункового механизма с треснувшим стержнем
Динамическое уравнение кривошипно-ползункового механизма установлено с использованием уравнения Лагранжа и второго закона Ньютона.Кривошипно-скользящий механизм со стержнем с открытой трещиной исследуется, а затем устанавливается эквивалентная модель механики безмассовой торсионной пружиной для моделирования влияния трещины в стержне, а механизм стержня с трещиной делится на две подсистемы. Установлено динамическое уравнение кривошипно-шатунного механизма с трещинной штангой. Сравнивая результаты динамического анализа с трещиной в стержне и без нее, результаты показывают, что наличие трещины приводит к значительному изменению характеристик движения ползуна.Рассчитанный максимальный показатель Ляпунова положителен, что свидетельствует о хаотичности движения ползуна в кривошипно-шатунном механизме с треснувшим штоком.
1. Введение
Точное соотношение между входом и выходом важно для кривошипно-ползункового механизма [1]. Например, в некоторых приложениях вращение кривошипа считается входом, а смещение ползунка — выходом. Поскольку механизм изготовлен не идеально, и всегда выходят трещины, которые, как известно, являются источником снижения надежности и точности системы [2, 3].Кроме того, сложно рассчитать влияние напрямую по нормальной формуле, если в стержне есть трещина. Такая трещина в стержне может привести к нелинейному поведению механизма, что должно влиять на динамику механизма, когда стержень приводится в действие в соответствии с вращением кривошипа. Итак, это поведение следует изучить. Jin Zeng, HuiMa, Wensheng Zhang и RangchunWen смешивают элементы, комбинируя балочные элементы и твердотельные элементы, для создания модели конечных элементов (КЭ) для консольных балок с трещинами и используют коэффициент повреждения площади для оценки уровней трещин [4].Уго Андресус и Паоло Казини использовали двухмерный четырехугольник для моделирования балки, затем были получены собственные частоты (и соответствующие формы колебаний) треснувшей консольной балки [5], и они также использовали двумерные конечные элементы для рассмотрения консольной балки с асимметричную краевую трещину в качестве задачи планирования, а затем сделайте вывод о поведении «дышащей» трещины, которая моделируется как контактная задача без трения [6, 7]. Михай Дюпак и Дэвид Бил моделируют трещину в ограждении безмассовой крутильной пружиной, а кривошипно-скользящий механизм моделируется одним уравнением движения [8].Андреа Карпинтери, Андреа Спаньоли и Сабрина Вантадори создают общее линейное правило упрочнения для волокон и линейно-упругий закон для матрицы, чтобы принять модель упруго-пластического перекрытия трещин [9]. О. Джаннини, П. Касини и Ф. Вестрони используют конечный элемент, который имеет билинейную матрицу элементов с разрывом, проходящим через начало координат, для моделирования зоны трещин в балке [10]. Пьер Франческо Каччола и Джузеппе Мусколино моделируют балку с трещинами с помощью конечных элементов, в которых модель замыкающей трещины используется для описания поврежденного элемента [11].Уго Андреаус, Паоло Барагатти, Паоло Казини и Даниэла Яковьелло представляют вейвлет-анализ для обнаружения и количественной оценки трещин в балках, основанный на статическом методе, после чего эффективность пространственного вейвлет-преобразования доказана после сравнения с экспериментальным исследованием [12]. Меньшикова, Александр В. Меньшиков и Игорь А. Гуз используют метод граничного интегрального уравнения для решения задачи механики разрушения, и они накладывают ограничения на нормальную и касательную составляющие контактной силы и векторы разрыва смещения для учета контактного взаимодействия. берегов трещины [13].
В данной работе создана новая идея по разделению кривошипно-шатунного механизма на две подсистемы по точке трещины, при этом трещина моделируется безмассовой крутильной пружиной. Треснувший стержень моделируется как два последовательных равных стержня, соединенных безмассовой торсионной пружиной. В этом методе намного проще смоделировать систему с множественными взломами и проще программировать на языке C. Сравнивая с результатами анализа кривошипно-шатунного механизма с трещиной и без трещины, сделан вывод о необходимости изучения влияния трещины при анализе динамических характеристик механической системы и вибрационной характеристики.
2. Анализ движения кривошипно-ползункового механизма
Для изучения разницы в динамическом движении кривошипно-ползункового механизма с трещиной в штоке и без нее, будет создано уравнение и проведено моделирование на основе расчета.
2.1. Уравнение движения кривошипно-ползунного механизма без трещины в штоке
Кривошипно-ползунковый механизм без трещины в штоке смоделирован на рисунке 1 для изучения эффекта динамического движения. Считается, что циклический изгибающий момент M приводит в движение механизм, а стержни OA и AB считаются жесткими.Движение механизма можно записать в виде уравнения Лагранжа и второго закона Ньютона [14–17].
Для этого механизма с одной степенью свободы обозначенное значение φ устанавливается как переменная в системе, а M — внешний момент. Угол поворота кривошипа φ — это угол между стержнем OA и горизонтальным направлением. Длина стержня OA составляет л 1 , тогда длина стержня AB составляет l 2 .Масса стержня OA составляет м 1 , а масса стержня AB м 2 . Инерционная масса стержня ОА равна. Инерционная масса стержня AB равна .Центральная скорость стержня AB равна, а его центральная угловая скорость равна. представляет скорость ползуна B. Полная кинетическая энергия равна, где T 1 — кинетическая энергия стержня OA, T 2 — кинетическая энергия стержня AB и T 3 — кинетическая энергия ползуна B.Кинетическую энергию кривошипно-ползунного механизма можно рассчитать следующим образом: Обобщенная сила может быть записана как Дифференциальное уравнение движения Лагранжа для кривошипно-ползункового механизма без трещин можно записать следующим образом [18–21]: Решение для функции дается следующим образом :
2.2. Уравнение движения кривошипно-ползунного механизма с трещиной в стержне
Кривошипно-скользящий механизм с трещиной в штоке смоделирован на рисунке 2 для изучения эффекта динамического движения. Считается, что стержень AB состоит из двух стержней AC и CB.Точка трещины C находится в середине стержня AB. Считается, что циклический изгибающий момент M приводит в движение механизм.
2.2.1. Система 1 и Система 2 Динамические уравнения
Кривошипно-скользящий механизм рассматривается как система 1 и система 2, которые разделены трещиной. Эквивалентная механическая модель трещины может быть установлена безмассовой крутильной пружиной [22, 23].
Для системы 1 есть две степени свободы; два назначенных значения и устанавливаются как переменные в системе.Угол поворота кривошипа — это угол между стержнем OA и горизонтальным направлением. — угол между стержнем AC и горизонтальным направлением. Центральная скорость стержня AC равна, а его центральная угловая скорость равна. Масса стержня АО составляет 1 м, а стержня АВ — 2 м. Поскольку стержень AO и стержень AB считаются равномерным распределением материала, масса стержня AC равна 2 м. Полная кинетическая энергия для системы 1 равна, где T 1 — кинетическая энергия стержня OA, T 2 — кинетическая энергия стержня AC.Кинетическую энергию системы 1 можно рассчитать по следующей формуле: Обобщенная сила может быть записана как Можно записать дифференциальное уравнение движения Лагранжа следующим образом [24]: Решение для функции дается следующим образом: Для системы 2 то же, что и В системе 1 обобщенная сила может быть записана как Дифференциальное уравнение Лагранжа можно записать следующим образом: Решение функции задается следующим образом: масса стержня CB равна, а m 3 — масса ползуна B. энергия стержня CB.- угол между стержнем CB и горизонтальным направлением. S — расстояние для ползуна B. Центральная скорость стержня CB равна, а его центральная угловая скорость равна. F — внешнее усилие на ползуне B.
2.2.2. Расчет стержня с трещиной
Стержень AB считается гибким, поэтому для моделирования трещины безмассовой крутильной пружиной [25–31], которая показана на рисунке 3. Рисунок 3 (a) показывает размер трещины в стержне, и Рисунок 3 (b) относится к торсионной пружине.
(a) Размер трещины в стержне
(b) Торсионная пружина
(a) Размер трещины в стержне
(b) Торсионная пружина
Уравнение кривой прогиба: обобщенная сила, EI — жесткость на изгиб.
Решение (12): где y (x) — прогиб, а угол изгиба поперечного сечения составляет θ (x), изгибающий момент равен M (x), и можно рассчитать силу сдвига следующим образом [32] : Гибкий стержень считается согласованным по прогибу, изгибающему моменту и усилию сдвига, поэтому относительный угол крутильной пружины можно записать как где — относительный угол между верхним стержнем и положением трещины, а — относительный угол между нижним стержнем. и положение трещины.Изгибающий момент крутильной пружины — это где C — гибкость поворотной пружины, на которую могут влиять глубина трещины d и высота поперечного сечения h [30, 33, 34]. Тогда уравнение движения кривошипно-шатунного механизма с трещину в штоке можно рассчитать следующим образом:
3. Сравнение движения кривошипно-ползункового механизма с трещиной в штоке и без нее
Моделирование кривошипно-ползункового механизма с трещиной в штоке и без нее выполняется на основе расчет верхнего уравнения.Механизм приводится в действие циклическим изгибающим моментом с обычной угловой скоростью 300 об / мин (оборот в минуту), что означает, что кривошип приводится в движение один цикл каждые 0,2 секунды. Параметры трещины, использованные в расчетах, следующие: глубина трещины d = 6 мм и высота поперечного сечения h = 30 мм. Сводка свойств экспериментальной модели кривошипа приведена в таблице 1.
Мы изучили влияние гибкости шатуна, длины кривошипа и массы ползуна на динамическое поведение механизма. 3.1 Длина шатунаМалые углы поворота коленвала относительно длины шатуна приводят к меньшей амплитуде вибрации и более периодическому результату. 3,2 Масса ползунаПо мере уменьшения массы ползуна амплитуда колебаний шатуна увеличивается и получается непредсказуемый ответ как по углу поворота кривошипа механизма, так и по амплитуде вибрации. 3.3 Гибкость шатунаУвеличение EI приводит к более жесткому механизму, и амплитуда вибрации уменьшается, как и ожидалось.Диаграмма θ в фазовой плоскости показывает более периодическую реакцию. 3,4 Постоянная угловая скорость кривошипаУчет постоянной угловой скорости кривошипа исключает одно из дифференциальных динамических уравнений второго порядка, поскольку угол поворота кривошипа известен в каждый момент времени. В этой ситуации интерес представляет амплитуда колебаний шатуна. Изучается частотная характеристика амплитуды вибрации в зависимости от параметров механизма при постоянной угловой скорости кривошипа.Амплитуда колебаний шатуна отложена относительно безразмерной угловой скорости кривошипа (рис. 2–4). где ω1 — первая собственная частота стержневой балки. При Ω = 1 механизм резонирует. В зависимости от параметров механизма значение пика вибрации на резонансной частоте различается. Отклик в фазовой плоскости при Ω = 1 показан на рис. 5, что указывает на неустойчивый фокус и проясняет нестабильность механизма.Рис.2 (а) диаграмма фазовой плоскости θ ( r = 0,003), (б) диаграмма фазовой плоскости θ ( r = 0,1), (в) диаграмма фазовой плоскости q 1 ( r = 0,003), и (d) диаграмма фазовой плоскости q 1 ( r = 0,1). Рис.2 (а) Диаграмма в фазовой плоскости θ ( r = 0,003), (б) диаграмма в фазовой плоскости для θ ( r = 0,1), (в) диаграмма в фазовой плоскости для q 1 ( r = 0.003), и (d) диаграмма фазовой плоскости q 1 ( r = 0,1). Рис.3 (a) Диаграмма в фазовой плоскости для θ (ms = 5), (b) диаграмма в фазовой плоскости для θ (ms = 0,5), (c) диаграмма в фазовой плоскости для q 1 (ms = 5), и (d) диаграмма фазовой плоскости q 1 (ms = 0,5). Рис.3 (а) Диаграмма в фазовой плоскости θ (мс = 5), (б) диаграмма в фазовой плоскости для θ (мс = 0,5), (в) диаграмма в фазовой плоскости для q 1 (мс = 5), и (d) диаграмма фазовой плоскости q 1 (ms = 0.5). Рис. 4 (а) Диаграмма в фазовой плоскости для θ ( EI = 0,2), (б) диаграмма в фазовой плоскости для θ ( EI = 20), (в) диаграмма в фазовой плоскости для q 1 ( EI = 0,2), и (d) диаграмма фазовой плоскости для q 1 ( EI = 20). Рис.4 (а) Диаграмма в фазовой плоскости θ ( EI = 0,2), (б) диаграмма в фазовой плоскости для θ ( EI = 20), (в) диаграмма в фазовой плоскости для q 1 ( EI = 0.2) и (d) диаграмма фазовой плоскости q 1 ( EI = 20). Рис. 5 Диаграмма амплитуды колебаний в фазовой плоскости при Ω = 1. Рис. 5 Диаграмма амплитуды колебаний в фазовой плоскости при Ω = 1. Частотная характеристика амплитуды колебаний шатуна изображена на рис. 6 для небольшой длины кривошипа ( r = 0,003 м и ms = 0,5 кг). С учетом параметров механизма проведено сравнительное исследование АЧХ колебаний шатуна (рис.7). Пика резонанса усиливается с увеличением длины кривошипа. Также достаточно большая длина кривошипа приводит к нестабильности механизма на высоких частотах. Другими словами, увеличение длины кривошипа снижает критическую угловую скорость. Рис. 6 АЧХ функция амплитуды колебаний. Рис. 6 АЧХ функция амплитуды вибрации. Рис. 7 Зависимость АЧХ от параметров механизма. Рис. 7 Зависимость АЧХ от параметров механизма. Затем строится диаграмма амплитуды вибрации в фазовой плоскости и сравнивается для каждого Ω. 4 Конструкция контроллераДля разработки контроллера для подавления упругодинамических колебаний гибкого шатуна разработаны два типа контроллеров. Один основан на методе линеаризации с обратной связью, а другой — на контроллере скользящего режима, который представляет собой надежный метод управления. Выше были выведены два вида динамических уравнений. В первом случае угол поворота коленчатого вала и его производные рассматриваются как состояния динамического уравнения и связаны с прогибом гибкого шатуна. Для этого случая разработан контроллер, основанный на подходе с обратной связью, и упругодинамические колебания гибкого шатуна подавляются, а угол поворота кривошипа и угловые скорости отслеживаются по желаемой синусоидальной траектории. Во втором динамическом уравнении учитывается постоянная угловая скорость кривошипа, и в уравнении неизвестны только прогиб упругого рычага и его производная.В этом случае реализован регулятор скользящего режима для устранения и подавления вибраций очень гибкого шатуна. Считается, что входные управляющие сигналы подаются электродвигателем, созданным в месте заземления кривошипа, и двумя слоями пьезоэлектрической пленки, прикрепленными к верхней и нижней поверхностям шатуна. Пьезоэлектрические элементы оказывают на луч распределенный момент, который пропорционален приложенному к ним напряжению. Этот момент зависит от нескольких параметров, таких как диэлектрический коэффициент, упругость и толщина пьезоэлемента и шатуна.Значение момента определяется выражением [18, 19]M1 = (Eawatatb) γγ + 6Λ, γ = EbwbtbEawataΛ = d31taV (14) где Eb, wb и tb — модуль упругости, толщина в направлении Y и толщина на Z направление алюминиевой балки соответственно. Ea, wa и ta — модуль упругости и толщина пьезоактуаторов. d31, — диэлектрический коэффициент, а В, — напряжение, приложенное к пьезоэлементу.Возвращаясь к методу Эйлера – Лагранжа при выводе динамических уравнений, этот момент возникает как момент в правой части уравнения, связанный с прогибом гибкой соединительной тяги, которая рассматривается в данном исследовании как управляющее воздействие (рис.8). Рис. 8 Недолет при определенной угловой скорости. Рис. 8 Недолет при определенной угловой скорости. Отклик механизма разомкнутого контура при приложении постоянного входного крутящего момента к кривошипу от двигателя изображен на рис. 9, который указывает отклонение в средней точке гибкого шатуна. Крутящий момент двигателя появляется только в дифференциальном уравнении первого второго порядка, связанном с углом поворота коленчатого вала.Поскольку уравнения движения гибкого ползуна-кривошипа связаны вместе, вращение кривошипа вызывает вибрацию в шатуне. Рис. 9 Отклик разомкнутого контура отклонения средней точки гибкого шатуна. Рис. 9 Отклик разомкнутого контура на отклонение средней точки гибкого шатуна. 4.1 Конструкция контроллера с использованием метода линеаризации обратной связиОсновная идея в этом методе состоит в том, чтобы исключить нелинейные члены динамического уравнения гибкого ползункового кривошипно-шатунного механизма, используя обратную связь по состоянию и применяя соответствующий входной крутящий момент в системе. В этом разделе он предназначен для подавления вибраций упругого рычага, помимо получения постоянной угловой скорости для кривошипа. Это означает, что кривошип должен отслеживать желаемый синусоидальный путь. Двигатель прикладывает один из моментов, вычисленных с помощью метода линеаризации с обратной связью, а другой — пьезоэлементом при подаче соответствующего напряжения.τ1 = θ¨des − k1θ˜̇ − k2θ˜ (15) где θdes — это путь, по которому угол поворота кривошипа желательно отслеживать, а θ˜ — ошибка отслеживания.τ2 = −k1′q̇1 − k2′q1 (16)Желательно, чтобы q1 было равно нулю, поэтому qdes≡0, q˜1 = q1. k1, k2 — это параметры управления, которые гарантируют требуемое поведение замкнутого контура отклика системы. Выбирая k1 = 4 = 2ξωn, k2 = 4 = ωn2, получаем критический отклик на демпфирование. Реакции замкнутого контура механизма показаны на рис. 10. Контроллер включается через одну секунду. Рис.10 (a) Отклик в замкнутом контуре угла поворота коленчатого вала (с помощью метода линеаризации с обратной связью), (b) Отклик с обратной связью θ̇ (с помощью метода линеаризации с обратной связью), (c) Отклик с замкнутым контуром средней точки отклонение (через подход линеаризации обратной связи), (d) отклик q̇1 в замкнутом контуре (через подход линеаризации обратной связи), (e) диаграмма фазовой плоскости θ, (f) диаграмма фазовой плоскости q1. Рис.10 (a) Отклик в замкнутом контуре угла поворота коленчатого вала (с помощью метода линеаризации обратной связи), (b) Отклик в замкнутом контуре θ̇ (через подход линеаризации с обратной связью), (c) Отклик в замкнутом контуре среднего отклонение точки (через подход линеаризации обратной связи), (d) отклик q̇1 в замкнутом контуре (через подход линеаризации обратной связи), (e) диаграмма фазовой плоскости θ, (f) диаграмма фазовой плоскости q1. Замечено, что разработанный контроллер эффективно подавляет эластодинамические колебания гибкого шатуна, а угол поворота кривошипа и угловая скорость позволяют при необходимости отслеживать желаемый синусоидальный путь.Диаграмма фазовой плоскости угла поворота коленчатого вала также подтверждает периодический желаемый путь для кривошипа. 4.2 Конструкция контроллера в скользящем режимеУправление скользящим режимом — это переменная структура, а также надежный метод управления. В этом методе введено упрощение обозначений, которое позволяет заменять задачи n-го порядка эквивалентными задачами 1-го порядка, которыми очень легко управлять. Поверхность с ( t ), изменяющаяся во времени, определяется скалярным уравнением s (x,; t) = 0, где q˜1 — ошибка отслеживания.При подавлении упругодинамических колебаний кривошипно-шатунного механизма желаемый q1 равен нулю.Задача слежения за q˜1 → 0 эквивалентна приближению к поверхности скольжения и оставлению на ней. Действительно, s≡0 представляет собой линейное дифференциальное уравнение с единственной точкой равновесия q˜≡0. Положительно определенная функция Ляпанова определяется как производная от V (s), которая гарантирует стабильность и отслеживание системы. Входной управляющий сигнал затем разрабатывается так, чтобы удовлетворять приведенному ниже условиюV̇ (s) = 12ddts2 = s.ṡ≤ − η | s | (20)Приведенное выше неравенство утверждает, что квадрат расстояния до поверхности, измеренный с помощью s2, уменьшается вдоль всех траекторий системы. Таким образом, он ограничивает траектории так, чтобы они указывали на поверхность скольжения s (t) . Закон управления, основанный на формуле. (20) реализовано на уравнении динамики гибкого шатуна, при этом предполагается постоянная угловая скорость.Mq¨1 + B (q1, q̇1) = τ2⇒q¨1 = F (q1, q̇1) + u (21) где F = −BM, а τ2 = MuV̇ (s) = 12ddts2 = s.ṡ ≤ − η | s | ⇒ {s <0, u = η − F − λq̇1s> 0, u = −η − F − λq̇1 (23)Ур.(23) подразумевает несогласный закон управления системой. Ответы замкнутого контура показали, что система по траектории приближается к поверхности скольжения и пытается удержаться на ней. Поскольку выполнение соответствующего переключения управления не происходит мгновенно, возникает дребезжание, что нежелательно на практике, поскольку оно связано с высокой управляющей активностью и выходом из строя пьезоактуаторов (рис. 11). Рис. 11 Фазовая диаграмма упругодинамических колебаний. Рис. 11 Диаграмма в фазовой плоскости упругодинамических колебаний. Здесь представлен новый закон управления, основанный на методе Филиппова для построения эквивалентной динамики для устранения дребезга. После выхода траекторий на поверхность скольжения к системе подается эквивалентный управляющий сигнал ueq, который можно интерпретировать как непрерывный закон управления. Отклики замкнутого контура системы, основанной на подходе скользящего режима и с учетом метода Филиппова, затем показаны на рис.12 и 13. Как показано на рисунках, вибрация устранена. В этой системе λ выбрано равным 3 и η = 0,5. Угловая скорость кривошипа ω = 0,4ω1. Рис. 12 (a) Ответ q1 в замкнутом контуре, (b) Отклик q̇1 в замкнутом контуре. Рис. 12 (a) Ответ q1 в замкнутом контуре, (b) Отклик q̇1 в замкнутом контуре. Рис. 13 Диаграмма фазовой плоскости q1 (дребезжание устранено). Фиг.13 Диаграмма фазовой плоскости q1 (дребезжание устранено). 5 ЗаключениеИсследовано динамическое поведение кривошипно-шатунного механизма с гибким шатуном. Уравнения движения механизма выводятся с использованием метода Эйлера – Лагранжа и метода суммирования мод. Динамический отклик системы зависит от параметров механизмов. Мы исследовали влияние длины кривошипа, гибкости шатуна и массы ползуна на динамическое поведение системы.Увеличение длины кривошипа приводит к увеличению амплитуды вибрации и непредсказуемому движению механизма. Уменьшение массы ползуна и увеличение гибкости шатуна приводят к тем же выводам. Заметив функцию частотной характеристики, увеличение длины кривошипа увеличивает значение подрыва в резонансе, а также снижает критическую скорость, что дестабилизирует механизм. Для подавления упругодинамических колебаний гибкого шатуна используются две схемы управления.Первая схема основана на линеаризации обратной связи, а вторая — на регуляторе скользящего режима. Затем производительность контроллера скользящего режима улучшается за счет использования метода Филиппова, и дребезжание устраняется. Управляющие воздействия прикладываются электродвигателем к заземляющему соединению кривошипа и двумя слоями пьезоэлектрической пленки, прикрепленными к верхней и нижней поверхностям шатуна. Список литературы[1]Хемили I. ,Romdhane L. Динамический анализ гибкого кривошипно-шатунного механизма с зазором .евро. J. Mech — A / Solids ,2008 ;27 :882 —898 . [2]Hsieh S. R. ,Shaw S. W. Динамическая стабильность и нелинейный резонанс гибкого шатуна: одномодовая модель .J. Sound Vib. ,1994 ;170 :25 —49 .[3]Jen-San C. ,Chu-Hsian C. Влияние длины кривошипа на динамическое поведение гибкого шатуна .ASME J. Vib. Акуст. ,2001 ;123 :318 —323 . [4]Zheng E. ,Zhou X. Моделирование гибкого кривошипно-ползункового механизма с зазором для закрытого высокоскоростного пресса система .мех. Мах. Теория ,2014 ;74 :10 —30 . [5]Reis VL ,Daniel GB ,Cavalca KL Динамический анализ планарного ползуна со смазкой коленчатого механизма и контактные эффекты Герца .мех. Мах. Теория ,2014 ;74 :257 —273 . [6]Muvengei O. ,Kihiu J. ,Ikua B. Численное исследование параметрических эффектов на динамический отклик плоских многочастичных систем с различными расположенными бесфрикционными шарнирами с поворотным зазором .мех. Мах. Теория ,2012 ;53 :30 —49 . [7]Zhang X. ,Mills JK ,Cleghorn WL Экспериментальная реализация управления движением в режиме вибрации 3 Гибкий параллельный манипулятор PRR с несколькими датчиками PZT .J. Vib. Control ,2010 . [8]Kao CC ,Chuang CW ,Fung RF Самонастраивающееся ПИД-регулирование в системе кривошипно-ползунковый механизм путем применения роя частиц Оптимизационный подход .Мехатроника ,2006 ;16 (8 )513 —522 . [9]Zhang X. ,Shao C. ,Li S. ,Xu D. ,Erdman A. G. Надежный контроль вибрации H∞ для систем гибкого рычажного механизма с пьезоэлектрическими датчиками и исполнительными механизмами .J. Sound Vib. ,2001 ;243 (1 )145 —155 . [10]Mansour A. K. Управление упругодинамическими колебаниями гибкого кривошипно-ползункового механизма с помощью -синтеза .Мехатроника ,2000 ;10 :649 —668 . [11]Каркоуб M. ,Yigit A. S. Контроль вибрации четырех стержневого механизма с очень гибкой муфтой .J. Sound Vib. ,1999 ;222 :171 —189 . [12]Sannah M. ,Smaili A. Активное управление эластодинамическими колебаниями четырехзвенной системы механизма с помощью интеллектуальной соединительной муфты оптимальное многопараметрическое управление: экспериментальная реализация .Пер. ASME J. Mech. Des ,1998 ;120 :316 —326 . [13]Пирбодаги T. ,Fesanghary M. ,Ahmadian MT Нелинейный анализ колебаний композитных пластин на нелинейно-упругих основаниях .J. Frankl. Inst. ,2011 ;348 :353 —368 . [14]Пирбодаги Т. ,Ahmadian M. T. ,Fesanghary M. О методе гомотопического анализа нелинейных колебаний балок .мех. Res. Commun. ,2009 ;36 :143 —148 . [15]Steen K. Сложные моды и частоты в затухающих структурных колебаниях .J. Sound Vib. ,2004 ;270 :981 —996 .[16]Пирбодаги T. ,Hoseini S. Нелинейные свободные колебания симметрично консервативной двухмассовой системы с кубической нелинейностью .J. Comput. Нелинейный Дин. ,2009 ;5 (1 )011006 . [17]Hoseini S. H. ,Pirbodaghi T. ,Ahmadian M. T. ,G. Farrahi 9H. О свободных колебаниях большой амплитуды конических балок: аналитический подход .мех. Res. Commun. ,2009 ;36 (8 )892 —897 . [18]Chopra I. Обзор современного состояния интеллектуальных структур и интегрированных систем .AIAA J. ,2002 ;40 :2145 —2187 . [19]Cameron B. ,Larry L. H. ,Spencer P. M. ,Mark S. E. Динамическое моделирование совместимых механизмов сжатия с постоянной силой .мех. Мах. Теория ,2003 ;38 :1469 —1487 .Общество инженеров CAD / CAM Экспериментальные наблюдения за гибким кривошипно-шатунным механизмом на очень высоких скоростяхЛиу Ф. В. и Пэн К. К., «Экспериментальный анализ вибрации механизмов», The Shock and Vibration Digest 24 , 1992, 3–10. Google ученый Лиу Ф. В. и Пэн К. К., «Экспериментальный анализ частотной характеристики гибких механизмов», Механизмы и теория машин 28 , 1992, 73–81. Google ученый Александр, Р. М. и Лоуренс, К. Л., «Экспериментальное исследование динамического отклика кластического механизма», ASME Journal of Engineering for Industry 18 , 1974, 268–274. Google ученый Джандраситс, В. Г. и Лоуэн, Г. Г., «Упруго-динамическое поведение балансира с противовесом и выступающей концевой массой в четырехрядном рычаге, часть II: применение и эксперимент», ASME Journal of Mechanical Design 101 , 1979, 89–97. Google ученый Сунг, К. К., Томпсон, Б. С., Син, Т. М., и Ван, К. Х., «Экспериментальное исследование нелинейной эластодинамической реакции рычажных механизмов», Механизм и теория машин 21 , 1986, 121–132. Google ученый Голебевски, Э. П. и Сэдлер, Дж. П., «Аналитическое и экспериментальное исследование упругих кривошипно-ползунковых механизмов» ASME Journal of Engineering for Industry 98 , 1976, 1266–1271. Google ученый Ляо, Д.X., Сун, К.К., Томпсон, Б.С., и Сунг, К., «Примечание о квазистатических откликах, динамических откликах и супергармонических откликах гибких связей: некоторые экспериментальные результаты ‘, ASME Paper No. 86-DET-146 , 1986 Fahrang, K., «Аналитические и экспериментальные исследования параметрической виброустойчивости в упругих механизмах», Ph.D. Диссертация, Университет Пердью, 1989. Бадлани М. и Кляйнхенц В., «Динамическая устойчивость упругих механизмов», Журнал инженерных наук ASME для промышленности 101 , 1979, 149–153. Google ученый Чжу, З. Г. и Чен, Ю., «Стабильность движения шатуна», Журнал ASME «Механизмы, передачи и автоматизация в проектировании» 105 , 1983, 637–640. Google ученый Фахранг К. и Мидха А., «Исследование параметрической виброустойчивости в кривошипно-шатунных механизмах с упругой муфтой», 1991 Техническая конференция по проектированию ASME , Майами, Флорида, Делавэр-Том. 37, 167–176. Таджбахш, И. Г. и Юнтис, К. Дж., «Динамическая устойчивость гибкого шатуна кривошипных механизмов ползуна», ASME Journal of Mechanisms, Transmission, and Automation in Design 108 , 1986, 1–10. Google ученый Бил Д. Г. и Ли С. В., «Исследование параметрической резонансной нестабильности в кривошипно-шатунном механизме с гибким стержнем и ползуном», 1991 Техническая конференция по проектированию ASME , Майами, Флорида, Делавэр-Том. 37, 161–166. Клегхорн, В. Л., Табаррок, Б., и Фентон, Р. Г., «Критические скорости движения и стабильность высокоскоростных гибких механизмов», Механизмы и теория машин 19 , 1984, 307–317. Google ученый Jasinski, P. W., Lee, H. C., and Sandor, G. N., «Стабильность и установившиеся колебания в высокоскоростном кривошипно-ползунковом механизме», ASME Journal of Applied Mechanisms 37 , 1970, 1069–1070. Google ученый Ли, С. В. и Бил, Д. Г., «Периодическая реакция и стабильность кривошипно-шатунных механизмов с гибким штоком ползуна», Техническая конференция по проектированию ASME , Феникс, Аризона, 13–16 сентября 1992 г. Хси, С. и Шоу, С. В., «Динамическая устойчивость и нелинейный резонанс гибкого шатуна: одномодовая модель», принято к публикации, Journal of Sound and Vibration . Хси, С. и Шоу, С. У., «Динамическая устойчивость и нелинейный резонанс гибкого шатуна: модель с непрерывными параметрами», Нелинейная динамика 4 , 1993, 573–603. Google ученый | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

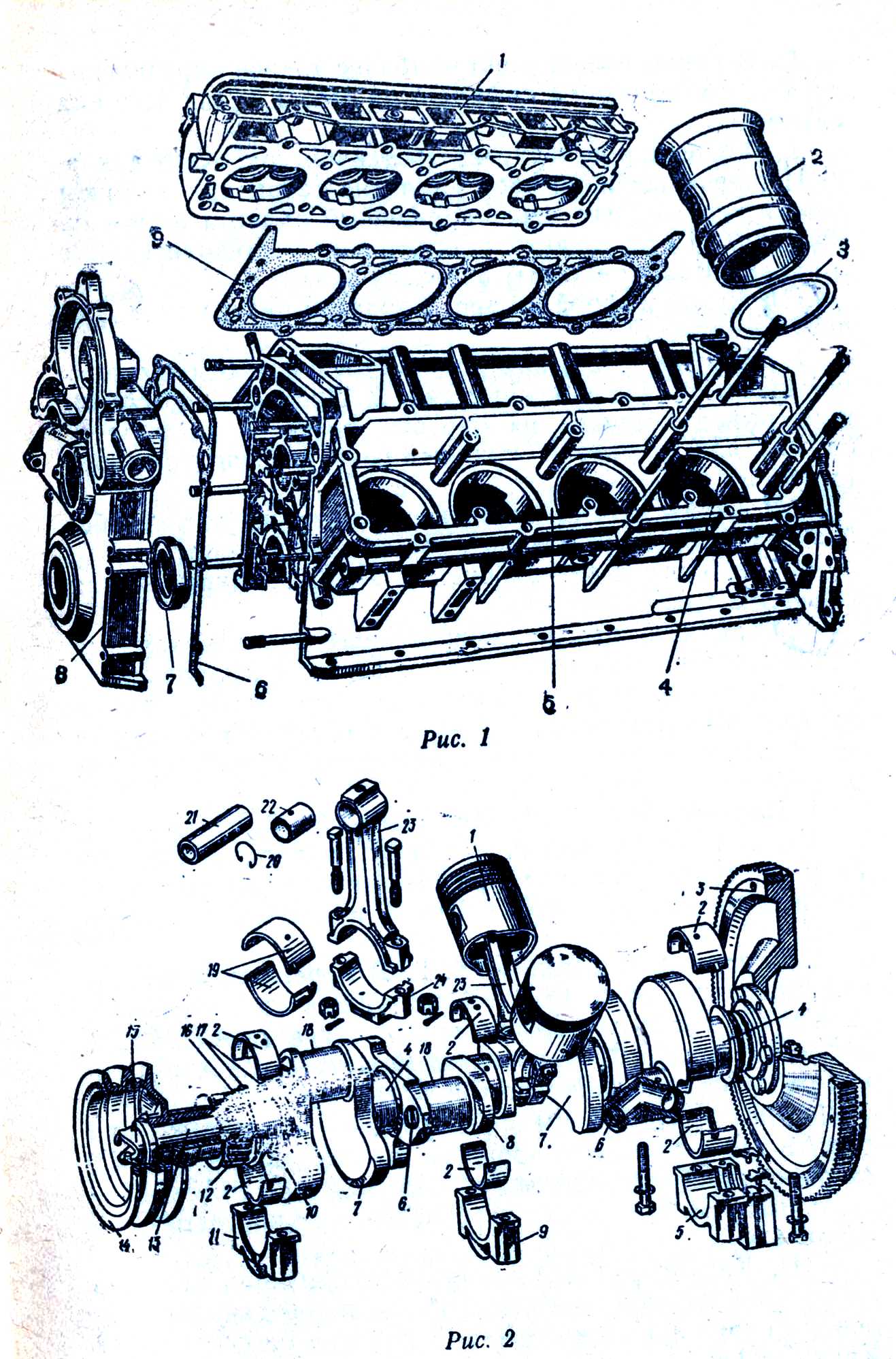 Для данной проблемы характерен звонкий стук вверху блока цилиндров при работающем моторе
Для данной проблемы характерен звонкий стук вверху блока цилиндров при работающем моторе